2.1轴对称再认识(一)随堂练习-北师大版数学五年级上册(含答案)
文档属性
| 名称 | 2.1轴对称再认识(一)随堂练习-北师大版数学五年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 337.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 08:04:47 | ||
图片预览




文档简介
2.1轴对称再认识(一)随堂练习-北师大版数学五年级上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下列每组图形中,对称轴数量相同的是( )。
A.长方形和正方形 B.等腰梯形和等腰三角形
C.长方形和平行四边形 D.正方形和圆
2.企业是社会经济发展非常重要的支柱,企业以生产或服务满足人们的物质和精神上的享受,它与人们的消费相辅相成、相互促进,良好的企业经济利益和所发挥的社会效益对社会经济的发展具有重要的促进作用。下面是我国一些企业的标志,其中是轴对称图形的有( )个。
A.1 B.2 C.3 D.4
3.下图的4个图形中,是轴对称图形的有( )个.
A.1 B.2 C.3 D.4
4.下面四个图形,( )的对称轴条数最多。
A.正方形 B.等边三角形
C.等腰梯形 D.直角等腰三角形
5.下图中是轴对称图形的有( )个.
A.1 B.2 C.3 D.4
6.下面图形中,( )的对称轴最多。
A. B. C. D.
7.在下列“禁毒”、“和平”、“节水”、“志愿者”这四个标志中,属于轴对称图形的是( )。
A. B. C. D.
8.下面的图案中,不是轴对称图形的有( )个。
A.4 B.3 C.2 D.10
二、填空题
9.圆有( )条对称轴,等腰梯形有( )条对称轴.
10.等边三角形有( )条对称轴,圆形有( )条对称轴,正方形有( )条对称轴,平行四边形有( )条对称轴.
11.和两个图形中,轴对称图形有( ),它的对称轴有( )条。
12.正方形有( )条对称轴,长方形有( )条对称轴,等腰三角形有( )条对称轴,等腰梯形有( )条对称轴,等边三角形有( )条对称轴,半圆形的对称轴有( )条。
13.假如一个图形对折后左右能( ),我们就把它叫做( )图形。
三、判断题
14.所有圆的都有无数条半径,无数条对称轴。( )
15.在对折的正方形彩纸上的任意位置打孔,将彩纸展开后,孔都是对称的。( )
16.梯形是轴对称图形。( )
17.我国赵州桥、法国埃菲尔铁塔都是对称的建筑。( )
四、解答题
18.小明将一张正方形纸对折两次,如下图所示,并在中央点打孔,再将它展开,请画出展开后的图形.
( )
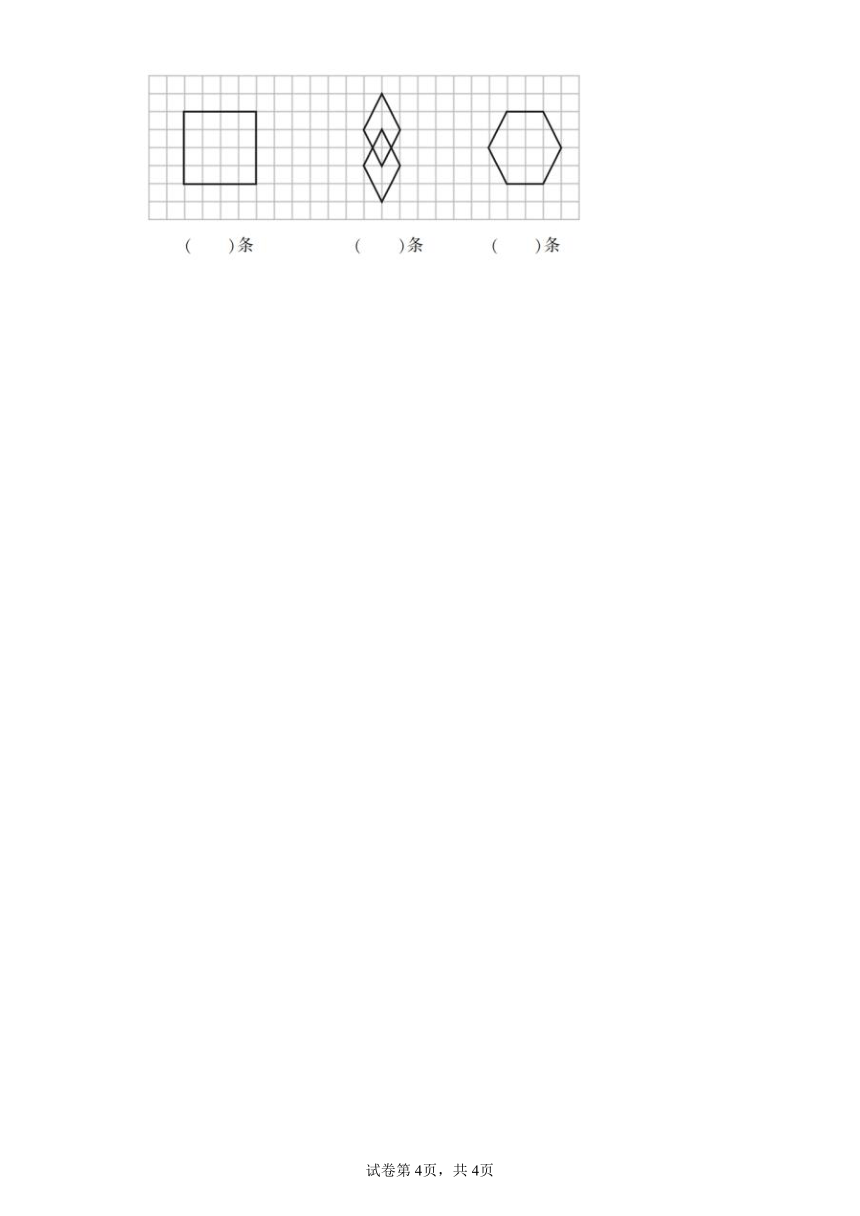
19.画一画,下面图形有几条对称轴?
( )条
( )条
20.画出如图轴对称图形的对称轴,并注明一共有_____条对称轴。
21.下列图案中是轴对称图形的是第几幅图?
22.下图中各有几条对称轴?画一画,写一写。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此解答。
【详解】A.长方形有2条对称轴;正方形有4条对称轴;对称轴数量不等;
B.等腰梯形有1条对称轴;等腰三角形有1条对称轴,等腰梯形与等腰三角形对称轴数量相同;
C.长方形有1条对称轴,平行四边形没有对称轴,对称轴数量不同;
D.正方形有4条对称轴,圆有无数条对称轴,对称轴数量不同。
故答案选:B
【点睛】本题考查轴对称图形的意义,以及对称轴的图形的特点。
2.B
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。据此解答即可。
【详解】如图:
所以第1个和第3个是轴对称图形,共2个。
故答案为:B
【点睛】此题考查了轴对称的意义及在实际当中的运用。
3.C
【详解】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此解答.
4.A
【分析】一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴。
【详解】A.正方形有4条对称轴;
B.等边三角形有3条对称轴;
C.等腰梯形有1条对称轴;
D.直角等腰三角形有1条对称轴。
4>3>1
正方形的对称轴条数最多。
故答案为:A
【点睛】利用轴对称图形的特点,找出轴对称图形的所有对称轴是解题的关键。
5.C
【解析】略
6.D
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可。
【详解】A. 对称轴有1条;
B.对称轴有4条;
C. 对称轴有6条;
D.有无数条对称轴。
故图形中对称轴最多的是。
故答案为:D
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
7.B
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此解答。
【详解】由轴对称图形的意义可知:属于轴对称图形。
故答案为:B
【点睛】本题主要考查轴对称图形的认识与辨认。
8.C
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此进行判断即可。
【详解】,这三个图形是轴对称图形,、这两个图形不是轴对称图形。
故答案为:C
【点睛】判断一个图案是否是轴对称图形的关键是看在这个图形中能否找到一条直线,使图形沿着这条直线对折后能够完全重合。
9. 无数 1
【解析】略
10. 3 无数 4 0
【解析】略
11. 正方形 4
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可。
【详解】
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
12. 4 2 1 1 3 1
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是它的对称轴,由此分别找出这几个图形的对称轴,据此解答。
【详解】正方形有4条对称轴,长方形有2条对称轴,等腰三角形有1条对称轴,等腰梯形有1条对称轴,等边三角形有3条对称轴,半圆形的对称轴有1条。
【点睛】本题考查轴对称图形的意义,根据轴对称的意义,找出对称轴的条数。
13. 完全重合 轴对称
【详解】根据轴对称图形的定义,假如一个图形对折后左右的图形能够完全重合,我们就把它叫做轴对称图形。
14.√
【分析】连接圆心和圆上任意一点的线段叫做半径。根据半径的定义可知,在圆上这样的点有无数个,所以一个圆的半径有无数条;依据轴对称图形的定义,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,据此即可进行判断。
【详解】所有圆的都有无数条半径,圆沿任何一条直径所在的直线对折,对折后的两部分都能完全重合,所以说圆有无数条对称轴。
故答案为:√
15.√
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形。
【详解】在对折的正方形彩纸上的任意位置打孔,将彩纸展开后,孔都是对称的。
故答案为:√
【点睛】本题考查了轴对称,折痕是这个正方形的对称轴。
16.×
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴。
【详解】只有等腰梯形是轴对称图形,还有许多不是轴对称图形的梯形。
故答案为:×
【点睛】本题考查了轴对称图形的辨别,要熟悉图形的特点。
17.√
【分析】我国赵州桥、法国埃菲尔铁塔都是沿着一条直线对折,直线两侧的部分能够完全重合,所以都是轴对称图形。
【详解】我国赵州桥、法国埃菲尔铁塔都是轴对称图形,即都是对称的建筑。
故答案为:√
【点睛】掌握轴对称图形的特征是解题的关键。
18.
【分析】正方形有4条对称轴,对折两次后的折痕是除了正方形两条对角线以外的两条对称轴,是这两条对称轴把大正方形分成了4个小正方形.还有大正方形经过两次对折是把大正方形按1:2缩小图;再把两次对折展开:如果不在中央打孔,是把小正方形按照2:1放大图.
【详解】将正方形纸对折两次:第一次对折是2个长方形重合;第二次对折后是4个小正方形重合,在中央打孔后展开成为含有4个圆孔的正方形.
19.;2;
;4
【分析】沿着直线对折能够完重合的图形是轴对称图形,折痕所在的直线就是对称轴。
【详解】,2;
,4。
【点睛】掌握对称轴的特征是解题的关键,注意画对称轴时,一般要用虚线。
20.;6
【分析】如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形。折痕所在的这条直线叫做对称轴。据此画图解答。
【详解】根据轴对称图形的定义可得:
,一共有6条对称轴。
【点睛】画对称轴的时候要按照一定的规律来画,防止漏画。
21.第④幅是轴对称图形
【分析】根据轴对称图形的定义:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形,据此解答。
【详解】根据分析可知,第④幅图沿中间直线左右对折,左右两边能够完全重合,所以是轴对称图形。
答:第④幅图是轴对称图形。
【点睛】本题考查轴对称图形的意义,根据轴对称图形的意义进行解答。
22.见详解。
【分析】依据轴对称图形的定义即可作答:一个图形沿某条直线对折,直线两旁的部分能够完全重合,这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴。
【详解】
【点睛】此题主要考查轴对称图形定义及对称轴的条数,熟记常见轴对称图形的对称轴条数即可解答。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下列每组图形中,对称轴数量相同的是( )。
A.长方形和正方形 B.等腰梯形和等腰三角形
C.长方形和平行四边形 D.正方形和圆
2.企业是社会经济发展非常重要的支柱,企业以生产或服务满足人们的物质和精神上的享受,它与人们的消费相辅相成、相互促进,良好的企业经济利益和所发挥的社会效益对社会经济的发展具有重要的促进作用。下面是我国一些企业的标志,其中是轴对称图形的有( )个。
A.1 B.2 C.3 D.4
3.下图的4个图形中,是轴对称图形的有( )个.
A.1 B.2 C.3 D.4
4.下面四个图形,( )的对称轴条数最多。
A.正方形 B.等边三角形
C.等腰梯形 D.直角等腰三角形
5.下图中是轴对称图形的有( )个.
A.1 B.2 C.3 D.4
6.下面图形中,( )的对称轴最多。
A. B. C. D.
7.在下列“禁毒”、“和平”、“节水”、“志愿者”这四个标志中,属于轴对称图形的是( )。
A. B. C. D.
8.下面的图案中,不是轴对称图形的有( )个。
A.4 B.3 C.2 D.10
二、填空题
9.圆有( )条对称轴,等腰梯形有( )条对称轴.
10.等边三角形有( )条对称轴,圆形有( )条对称轴,正方形有( )条对称轴,平行四边形有( )条对称轴.
11.和两个图形中,轴对称图形有( ),它的对称轴有( )条。
12.正方形有( )条对称轴,长方形有( )条对称轴,等腰三角形有( )条对称轴,等腰梯形有( )条对称轴,等边三角形有( )条对称轴,半圆形的对称轴有( )条。
13.假如一个图形对折后左右能( ),我们就把它叫做( )图形。
三、判断题
14.所有圆的都有无数条半径,无数条对称轴。( )
15.在对折的正方形彩纸上的任意位置打孔,将彩纸展开后,孔都是对称的。( )
16.梯形是轴对称图形。( )
17.我国赵州桥、法国埃菲尔铁塔都是对称的建筑。( )
四、解答题
18.小明将一张正方形纸对折两次,如下图所示,并在中央点打孔,再将它展开,请画出展开后的图形.
( )
19.画一画,下面图形有几条对称轴?
( )条
( )条
20.画出如图轴对称图形的对称轴,并注明一共有_____条对称轴。
21.下列图案中是轴对称图形的是第几幅图?
22.下图中各有几条对称轴?画一画,写一写。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此解答。
【详解】A.长方形有2条对称轴;正方形有4条对称轴;对称轴数量不等;
B.等腰梯形有1条对称轴;等腰三角形有1条对称轴,等腰梯形与等腰三角形对称轴数量相同;
C.长方形有1条对称轴,平行四边形没有对称轴,对称轴数量不同;
D.正方形有4条对称轴,圆有无数条对称轴,对称轴数量不同。
故答案选:B
【点睛】本题考查轴对称图形的意义,以及对称轴的图形的特点。
2.B
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。据此解答即可。
【详解】如图:
所以第1个和第3个是轴对称图形,共2个。
故答案为:B
【点睛】此题考查了轴对称的意义及在实际当中的运用。
3.C
【详解】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此解答.
4.A
【分析】一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴。
【详解】A.正方形有4条对称轴;
B.等边三角形有3条对称轴;
C.等腰梯形有1条对称轴;
D.直角等腰三角形有1条对称轴。
4>3>1
正方形的对称轴条数最多。
故答案为:A
【点睛】利用轴对称图形的特点,找出轴对称图形的所有对称轴是解题的关键。
5.C
【解析】略
6.D
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可。
【详解】A. 对称轴有1条;
B.对称轴有4条;
C. 对称轴有6条;
D.有无数条对称轴。
故图形中对称轴最多的是。
故答案为:D
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
7.B
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此解答。
【详解】由轴对称图形的意义可知:属于轴对称图形。
故答案为:B
【点睛】本题主要考查轴对称图形的认识与辨认。
8.C
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此进行判断即可。
【详解】,这三个图形是轴对称图形,、这两个图形不是轴对称图形。
故答案为:C
【点睛】判断一个图案是否是轴对称图形的关键是看在这个图形中能否找到一条直线,使图形沿着这条直线对折后能够完全重合。
9. 无数 1
【解析】略
10. 3 无数 4 0
【解析】略
11. 正方形 4
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可。
【详解】
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
12. 4 2 1 1 3 1
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是它的对称轴,由此分别找出这几个图形的对称轴,据此解答。
【详解】正方形有4条对称轴,长方形有2条对称轴,等腰三角形有1条对称轴,等腰梯形有1条对称轴,等边三角形有3条对称轴,半圆形的对称轴有1条。
【点睛】本题考查轴对称图形的意义,根据轴对称的意义,找出对称轴的条数。
13. 完全重合 轴对称
【详解】根据轴对称图形的定义,假如一个图形对折后左右的图形能够完全重合,我们就把它叫做轴对称图形。
14.√
【分析】连接圆心和圆上任意一点的线段叫做半径。根据半径的定义可知,在圆上这样的点有无数个,所以一个圆的半径有无数条;依据轴对称图形的定义,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,据此即可进行判断。
【详解】所有圆的都有无数条半径,圆沿任何一条直径所在的直线对折,对折后的两部分都能完全重合,所以说圆有无数条对称轴。
故答案为:√
15.√
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形。
【详解】在对折的正方形彩纸上的任意位置打孔,将彩纸展开后,孔都是对称的。
故答案为:√
【点睛】本题考查了轴对称,折痕是这个正方形的对称轴。
16.×
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴。
【详解】只有等腰梯形是轴对称图形,还有许多不是轴对称图形的梯形。
故答案为:×
【点睛】本题考查了轴对称图形的辨别,要熟悉图形的特点。
17.√
【分析】我国赵州桥、法国埃菲尔铁塔都是沿着一条直线对折,直线两侧的部分能够完全重合,所以都是轴对称图形。
【详解】我国赵州桥、法国埃菲尔铁塔都是轴对称图形,即都是对称的建筑。
故答案为:√
【点睛】掌握轴对称图形的特征是解题的关键。
18.
【分析】正方形有4条对称轴,对折两次后的折痕是除了正方形两条对角线以外的两条对称轴,是这两条对称轴把大正方形分成了4个小正方形.还有大正方形经过两次对折是把大正方形按1:2缩小图;再把两次对折展开:如果不在中央打孔,是把小正方形按照2:1放大图.
【详解】将正方形纸对折两次:第一次对折是2个长方形重合;第二次对折后是4个小正方形重合,在中央打孔后展开成为含有4个圆孔的正方形.
19.;2;
;4
【分析】沿着直线对折能够完重合的图形是轴对称图形,折痕所在的直线就是对称轴。
【详解】,2;
,4。
【点睛】掌握对称轴的特征是解题的关键,注意画对称轴时,一般要用虚线。
20.;6
【分析】如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形。折痕所在的这条直线叫做对称轴。据此画图解答。
【详解】根据轴对称图形的定义可得:
,一共有6条对称轴。
【点睛】画对称轴的时候要按照一定的规律来画,防止漏画。
21.第④幅是轴对称图形
【分析】根据轴对称图形的定义:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形,据此解答。
【详解】根据分析可知,第④幅图沿中间直线左右对折,左右两边能够完全重合,所以是轴对称图形。
答:第④幅图是轴对称图形。
【点睛】本题考查轴对称图形的意义,根据轴对称图形的意义进行解答。
22.见详解。
【分析】依据轴对称图形的定义即可作答:一个图形沿某条直线对折,直线两旁的部分能够完全重合,这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴。
【详解】
【点睛】此题主要考查轴对称图形定义及对称轴的条数,熟记常见轴对称图形的对称轴条数即可解答。
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
