数学八年级下青岛版6.4三角形的中位线定理课件1
文档属性
| 名称 | 数学八年级下青岛版6.4三角形的中位线定理课件1 |
|
|
| 格式 | zip | ||
| 文件大小 | 205.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-23 00:00:00 | ||
图片预览




文档简介
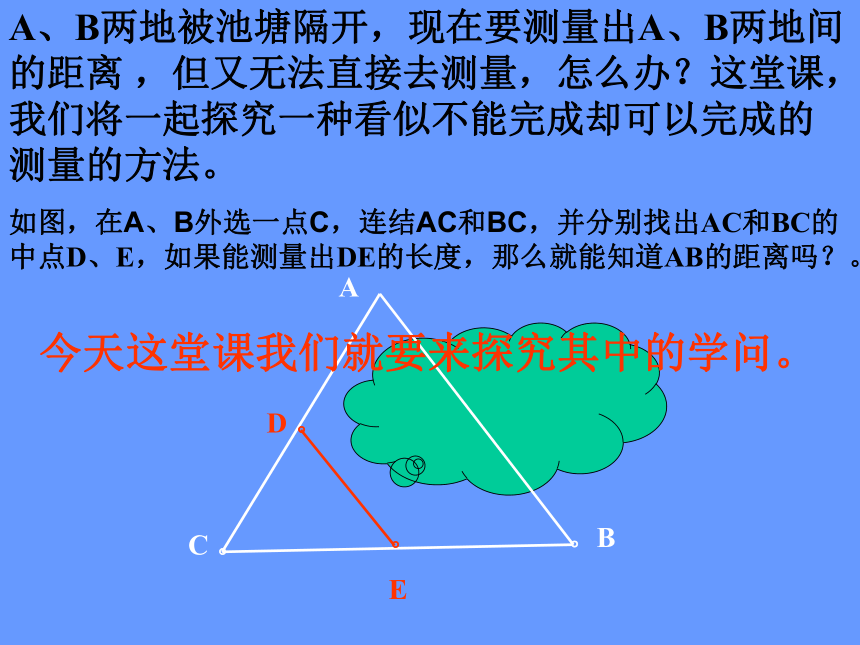
课件18张PPT。ABCDE三角形中位线A 。BC 。D 。。
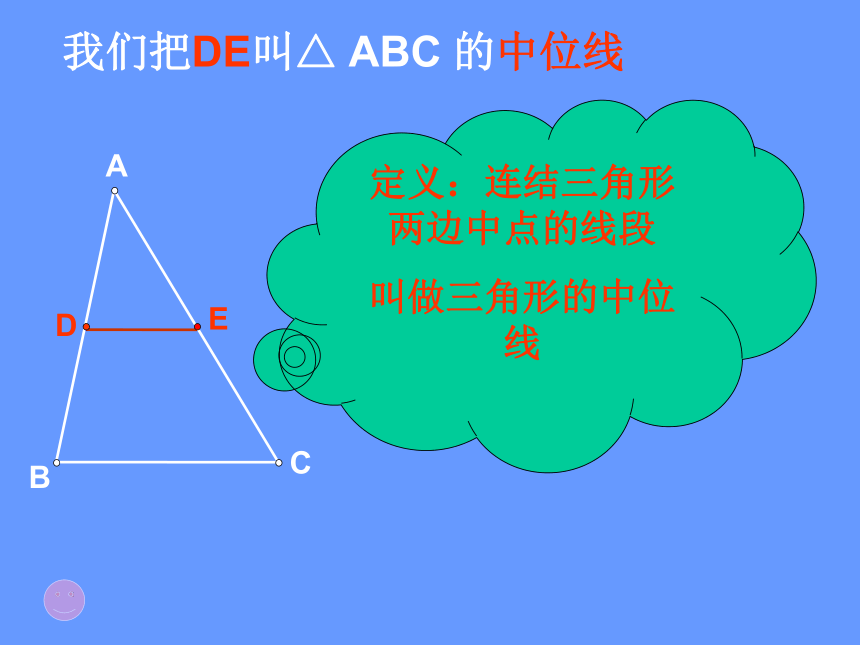
EA、B两地被池塘隔开,现在要测量出A、B两地间的距离 ,但又无法直接去测量,怎么办?这堂课,我们将一起探究一种看似不能完成却可以完成的测量的方法。如图,在A、B外选一点C,连结AC和BC,并分别找出AC和BC的中点D、E,如果能测量出DE的长度,那么就能知道AB的距离吗?。今天这堂课我们就要来探究其中的学问。
补充:(1)平行线等分线段定理推论 经过三角形一边的中点与另一边平行的直线,必平分第三边。几何语言:
在△ ABC中
∵ AD=DB,DE//BC
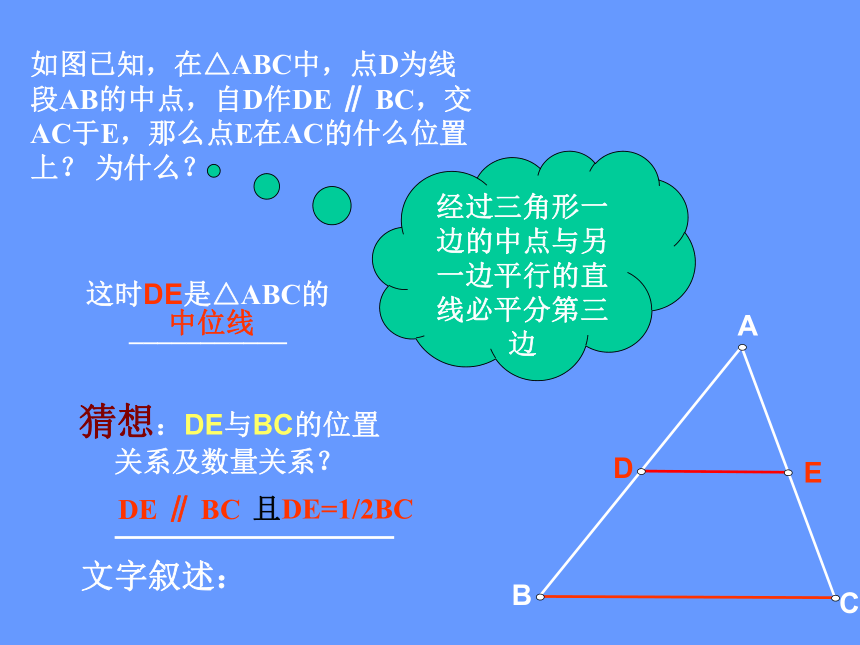
∴ AE=ECFCBAED定义:连结三角形两边中点的线段
叫做三角形的中位线
我们把DE叫△ ABC 的中位线 注意:三角形的中位线是连结三角形两边中点的线段三角形的中线是连结一个顶点和它的对边中点的线段三角形的中位线和中线区别: 理解三角形的中位线定义的两层含义:② ∵ DE为△ABC的中位线 ① ∵D、E分别为AB、AC的中点 ∴DE为△ABC的中位线∴ D、E分别为AB、AC的中点 一个三角形共有三条中位线。定义ABCD。。E。FABCDE经过三角形一边的中点与另一边平行的直线必平分第三边如图已知,在△ABC中,点D为线段AB的中点,自D作DE ∥ BC,交AC于E,那么点E在AC的什么位置上? 为什么?这时DE是△ABC的___________中位线猜想:DE与BC的位置关系及数量关系?DE ∥ BC且DE=1/2BC文字叙述:过D作DE’∥BC,交AC于E’点∵D为AB边上的中点所以DE’与DE重合,因此DE∥BC同样过D作DF∥AC,交BC于F∴BF=FC= 1/2BC (经过三角形一边的中点与
另一边平行的直线必平分第三边)∴四边形DECF是平行四边形∴DE=FC ∴ DE=1/2BCABCDEE’F证明方法1.三角形的中位线平行于第三边,并且等于第三边的 一半已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC ABCDEF证明方法2.:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥= CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC ABCEDFABCEDF常见的三种证法ABCDE’EF三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半。如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2用 途ABCDE***中点想到 中线、中位线1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 2.如图2:在△ABC中,D、E、F分别
是各边中点
EF=3cm,DF=4cm,DE=5cm,
则△ABC的周长= cm图1图260424ABCD。。EBACD 。。E。F543A 。。BC 。D。。
E3. 在A、B外选一点C,连结AC和BC,并分别找出
AC和BC的中点D、E,如果能测量出DE的长度,
也就能知道AB的距离了。为什么?如果测的DE
=20m,那么A、B两点间的距离是多少?为什么?
20404.例:求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形求证:四边形EFGH是平行四边形证明:连结AC∵AH=HD CG=GD∴HG∥AC(三角形的中位线平行于第三边,并且等于它的一半)同理EF∥AC∴HG∥EF且HG=EF∴四边形EFGH是平行四边形【例题】求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形。∵AH=HD,CG=GD∴HG//AC,HG= AC(三角形中位线定理)且EF=HG所以四边形EFGH是平行四边形∴ EF//HG, (1) 如图,AF=FD=DB,
FG∥DE∥BC,PE=1.5。
则DP= ———,BC= ———。34.591.5PABFGECD(2)已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△ HPN的周长等于—————,为△ ABC周长的——, 面积为△ABC面积的—— 提高练习:4.5 93、证明线段倍分关系的方法常有三种:CD = ? AB DE = ? CBBC = ? AB小 结三角形中位线定义三角形中位线定理三角形中位线定理用途 ⑴在四边形ABCD另加条件AC=BD, 四边形EFGH是_______,为什么?
⑵在四边形ABCD另加条件AC⊥BD,四边形EFGH是_____?为什么?
⑶若四边形EFGH是正方形,AC与BD应满足什么条件? 1. 连结BD 证:EH ∥= FG 2.连结AC、BD ,证:EF∥HG, EH∥FG
3.连结AC、BD, 证:EF=HG,EH=FG
EA、B两地被池塘隔开,现在要测量出A、B两地间的距离 ,但又无法直接去测量,怎么办?这堂课,我们将一起探究一种看似不能完成却可以完成的测量的方法。如图,在A、B外选一点C,连结AC和BC,并分别找出AC和BC的中点D、E,如果能测量出DE的长度,那么就能知道AB的距离吗?。今天这堂课我们就要来探究其中的学问。
补充:(1)平行线等分线段定理推论 经过三角形一边的中点与另一边平行的直线,必平分第三边。几何语言:
在△ ABC中
∵ AD=DB,DE//BC
∴ AE=ECFCBAED定义:连结三角形两边中点的线段
叫做三角形的中位线
我们把DE叫△ ABC 的中位线 注意:三角形的中位线是连结三角形两边中点的线段三角形的中线是连结一个顶点和它的对边中点的线段三角形的中位线和中线区别: 理解三角形的中位线定义的两层含义:② ∵ DE为△ABC的中位线 ① ∵D、E分别为AB、AC的中点 ∴DE为△ABC的中位线∴ D、E分别为AB、AC的中点 一个三角形共有三条中位线。定义ABCD。。E。FABCDE经过三角形一边的中点与另一边平行的直线必平分第三边如图已知,在△ABC中,点D为线段AB的中点,自D作DE ∥ BC,交AC于E,那么点E在AC的什么位置上? 为什么?这时DE是△ABC的___________中位线猜想:DE与BC的位置关系及数量关系?DE ∥ BC且DE=1/2BC文字叙述:过D作DE’∥BC,交AC于E’点∵D为AB边上的中点所以DE’与DE重合,因此DE∥BC同样过D作DF∥AC,交BC于F∴BF=FC= 1/2BC (经过三角形一边的中点与
另一边平行的直线必平分第三边)∴四边形DECF是平行四边形∴DE=FC ∴ DE=1/2BCABCDEE’F证明方法1.三角形的中位线平行于第三边,并且等于第三边的 一半已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC ABCDEF证明方法2.:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥= CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC ABCEDFABCEDF常见的三种证法ABCDE’EF三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半。如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2用 途ABCDE***中点想到 中线、中位线1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 2.如图2:在△ABC中,D、E、F分别
是各边中点
EF=3cm,DF=4cm,DE=5cm,
则△ABC的周长= cm图1图260424ABCD。。EBACD 。。E。F543A 。。BC 。D。。
E3. 在A、B外选一点C,连结AC和BC,并分别找出
AC和BC的中点D、E,如果能测量出DE的长度,
也就能知道AB的距离了。为什么?如果测的DE
=20m,那么A、B两点间的距离是多少?为什么?
20404.例:求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形求证:四边形EFGH是平行四边形证明:连结AC∵AH=HD CG=GD∴HG∥AC(三角形的中位线平行于第三边,并且等于它的一半)同理EF∥AC∴HG∥EF且HG=EF∴四边形EFGH是平行四边形【例题】求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形。∵AH=HD,CG=GD∴HG//AC,HG= AC(三角形中位线定理)且EF=HG所以四边形EFGH是平行四边形∴ EF//HG, (1) 如图,AF=FD=DB,
FG∥DE∥BC,PE=1.5。
则DP= ———,BC= ———。34.591.5PABFGECD(2)已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△ HPN的周长等于—————,为△ ABC周长的——, 面积为△ABC面积的—— 提高练习:4.5 93、证明线段倍分关系的方法常有三种:CD = ? AB DE = ? CBBC = ? AB小 结三角形中位线定义三角形中位线定理三角形中位线定理用途 ⑴在四边形ABCD另加条件AC=BD, 四边形EFGH是_______,为什么?
⑵在四边形ABCD另加条件AC⊥BD,四边形EFGH是_____?为什么?
⑶若四边形EFGH是正方形,AC与BD应满足什么条件? 1. 连结BD 证:EH ∥= FG 2.连结AC、BD ,证:EF∥HG, EH∥FG
3.连结AC、BD, 证:EF=HG,EH=FG
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
