数学七年级下青岛版9.3平行线的性质课件
文档属性
| 名称 | 数学七年级下青岛版9.3平行线的性质课件 |  | |
| 格式 | zip | ||
| 文件大小 | 342.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-23 11:06:22 | ||
图片预览



文档简介
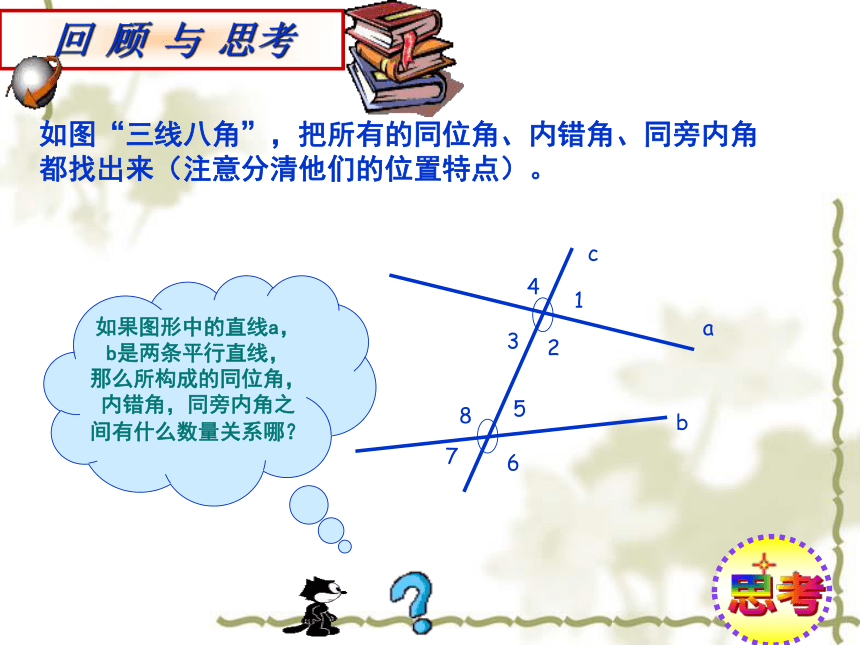
课件16张PPT。9.3平行线的性质回 顾 与 思考如图“三线八角”,把所有的同位角、内错角、同旁内角
都找出来(注意分清他们的位置特点)。acb41325876如果图形中的直线a,b是两条平行直线,那么所构成的同位角,内错角,同旁内角之间有什么数量关系哪? 思考学习目标:
1、探索平行线的性质,并能用文字语言、 符号语言表示性质。
2、能用性质进行推理和计算。
3、理解平行线之间的距离的概念。9.3平行线的性质两直线平行,同位角相等.平行线的性质1结论 两条平行线被第三条直线所截,
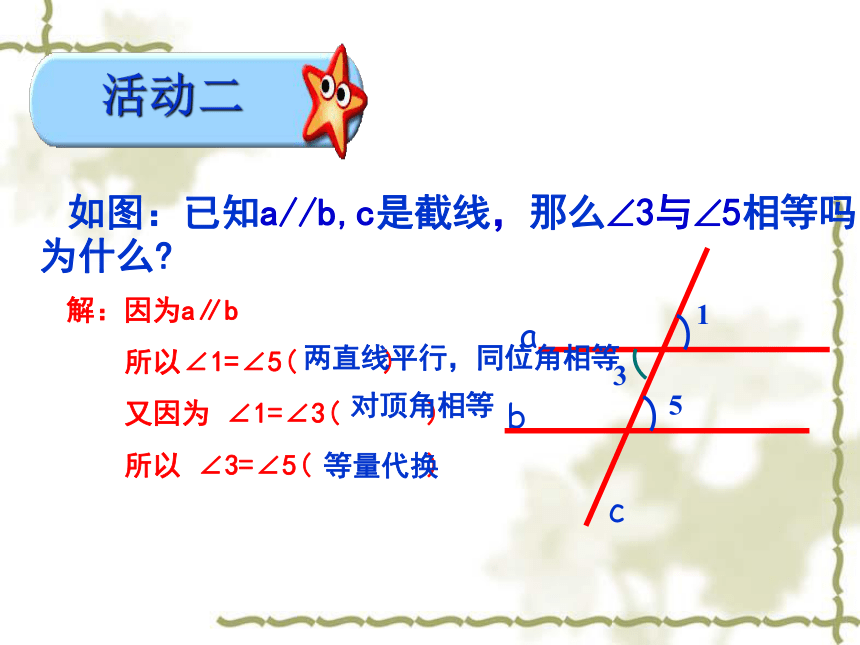
同位角相等.所以∠1=∠5.因为a∥b,简写为:符号语言:a∥b 如图:已知a//b,c是截线,那么?3与?5相等吗?
为什么?解:因为a∥b
所以∠1=∠5( )
又因为 ∠1=∠3( )
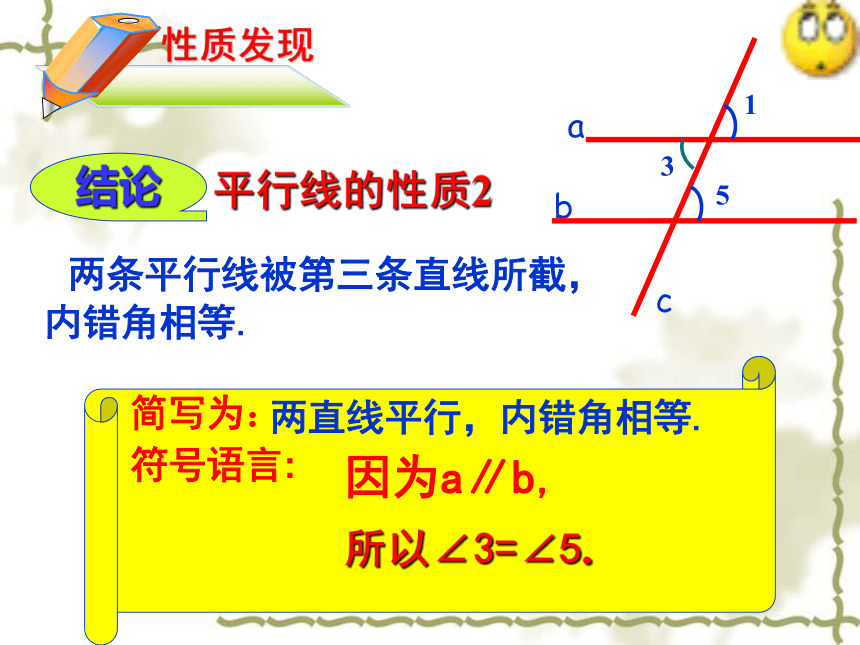
所以 ∠3=∠5( ) 活动二两直线平行,同位角相等对顶角相等等量代换两直线平行,内错角相等.平行线的性质2结论 两条平行线被第三条直线所截,
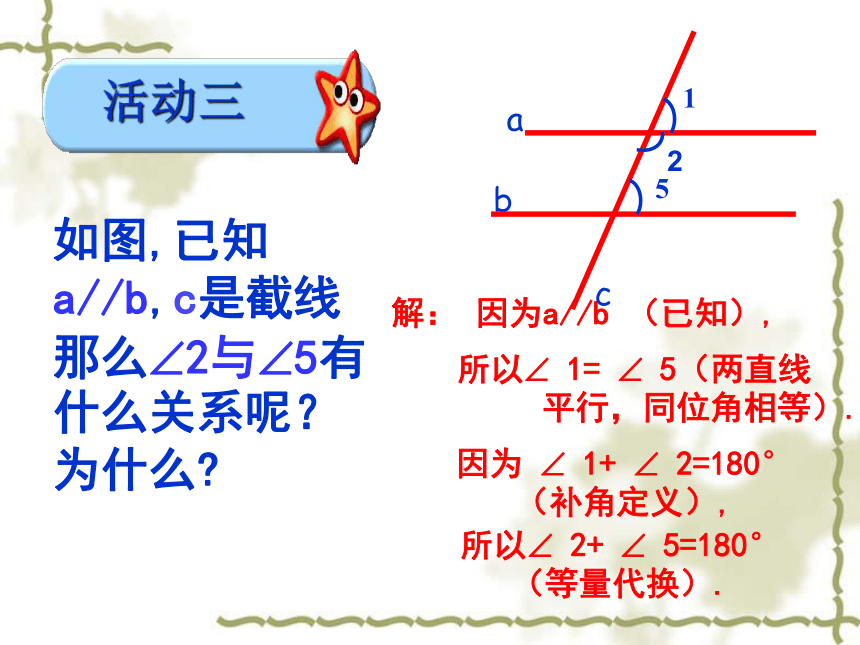
内错角相等.所以∠3=∠5.因为a∥b,符号语言:简写为:解: 因为a//b (已知), 如图,已知a//b,c是截线那么?2与?5有什么关系呢?为什么? 活动三所以? 1= ? 5(两直线
平行,同位角相等). 因为 ? 1+ ? 2=180° (补角定义), 所以? 2+ ? 5=180° (等量代换).两直线平行,同旁内角互补.平行线的性质3结论 两条平行线被第三条直线所截,
同旁内角互补.所以? 2+ ? 5=180°.因为a∥b,符号语言:简写为:典例示范如图,已知直线a∥b,c∥d,∠1 = 1060,
求∠2, ∠3的度数. 解:因为a∥b (已知),
所以∠1=∠2(两直线平行,内错
角相等)
因为 ∠1= 1060(已知),
所以 ∠2= 1060 (等量代换).;
因为c∥d(已知),
所以∠3=∠2(两直线平行, 同位角相等).
又因为 ∠2= 1060(已证)
所以∠3=1060 (等量代换)
c 热身练习
1、如图 直线a∥b,若∠1= 1180 ,求∠2的度数。
2、如图 如果DE∥AB 那么
∠A+ ∠————— =180°( )
∠B=∠ ( )b12acABCED 交流与发现 按要求画图:
(1)如图 l1 和l2平行,在l1上任取一点A,过点A画l2的垂线AC,垂足是C,
那么AC与l1垂直吗?为什么?
(2)在l1上再任取一点B,按同样的方法画到l2的垂线段BD,
那么AC和BD位置、大小各有什么关系?为什么?
(3)再画无数条这样的垂线段,你能发现什么?
我们把这样的垂线段(AC或BD)的长度叫做这两条平行线之间的距离。定义:如果两条直线平行,那么其中一条直线
上每个点到另一条直线的距离都相等。这个距离,
叫做两条平行线之间的距离。想一想:
今天你学习了平行线间的距离,那么你会测量数学教材的
厚度吗?与同位交流一下,看谁先得出答案。 l1l2丰收园通过本堂课的学习你有哪些收获?与同伴交流小结与回顾 当堂达标1、如图:AB∥DE,∠B=500,则∠1= ∠2= ∠3= 。 ABCDE1232、结合右边图形写出推理过程
因为AB∥CD(已知)
所以 ∠1=∠ ( )
又因为∠3=∠2( )
所以∠1=∠ (等量代换)
因为∠4+∠2= (补角定义)
所以∠4+∠ =180°(等量代换)ABCDEF13243、如图,直线a∥b,点B在直线b上,且AB⊥BC,
∠1=55°,则∠2=
ABC2b1a4、如图AB∥CD,AD交BC于点O,∠A=500,
∠AOB=1000。求∠C的度数。ABCOD 作业布置必做题:教材第37页习题9.3第1、3题。
选做题:教材第37页习题9.3第4、5题。祝同学们学习进步谢谢大家!
都找出来(注意分清他们的位置特点)。acb41325876如果图形中的直线a,b是两条平行直线,那么所构成的同位角,内错角,同旁内角之间有什么数量关系哪? 思考学习目标:
1、探索平行线的性质,并能用文字语言、 符号语言表示性质。
2、能用性质进行推理和计算。
3、理解平行线之间的距离的概念。9.3平行线的性质两直线平行,同位角相等.平行线的性质1结论 两条平行线被第三条直线所截,
同位角相等.所以∠1=∠5.因为a∥b,简写为:符号语言:a∥b 如图:已知a//b,c是截线,那么?3与?5相等吗?
为什么?解:因为a∥b
所以∠1=∠5( )
又因为 ∠1=∠3( )
所以 ∠3=∠5( ) 活动二两直线平行,同位角相等对顶角相等等量代换两直线平行,内错角相等.平行线的性质2结论 两条平行线被第三条直线所截,
内错角相等.所以∠3=∠5.因为a∥b,符号语言:简写为:解: 因为a//b (已知), 如图,已知a//b,c是截线那么?2与?5有什么关系呢?为什么? 活动三所以? 1= ? 5(两直线
平行,同位角相等). 因为 ? 1+ ? 2=180° (补角定义), 所以? 2+ ? 5=180° (等量代换).两直线平行,同旁内角互补.平行线的性质3结论 两条平行线被第三条直线所截,
同旁内角互补.所以? 2+ ? 5=180°.因为a∥b,符号语言:简写为:典例示范如图,已知直线a∥b,c∥d,∠1 = 1060,
求∠2, ∠3的度数. 解:因为a∥b (已知),
所以∠1=∠2(两直线平行,内错
角相等)
因为 ∠1= 1060(已知),
所以 ∠2= 1060 (等量代换).;
因为c∥d(已知),
所以∠3=∠2(两直线平行, 同位角相等).
又因为 ∠2= 1060(已证)
所以∠3=1060 (等量代换)
c 热身练习
1、如图 直线a∥b,若∠1= 1180 ,求∠2的度数。
2、如图 如果DE∥AB 那么
∠A+ ∠————— =180°( )
∠B=∠ ( )b12acABCED 交流与发现 按要求画图:
(1)如图 l1 和l2平行,在l1上任取一点A,过点A画l2的垂线AC,垂足是C,
那么AC与l1垂直吗?为什么?
(2)在l1上再任取一点B,按同样的方法画到l2的垂线段BD,
那么AC和BD位置、大小各有什么关系?为什么?
(3)再画无数条这样的垂线段,你能发现什么?
我们把这样的垂线段(AC或BD)的长度叫做这两条平行线之间的距离。定义:如果两条直线平行,那么其中一条直线
上每个点到另一条直线的距离都相等。这个距离,
叫做两条平行线之间的距离。想一想:
今天你学习了平行线间的距离,那么你会测量数学教材的
厚度吗?与同位交流一下,看谁先得出答案。 l1l2丰收园通过本堂课的学习你有哪些收获?与同伴交流小结与回顾 当堂达标1、如图:AB∥DE,∠B=500,则∠1= ∠2= ∠3= 。 ABCDE1232、结合右边图形写出推理过程
因为AB∥CD(已知)
所以 ∠1=∠ ( )
又因为∠3=∠2( )
所以∠1=∠ (等量代换)
因为∠4+∠2= (补角定义)
所以∠4+∠ =180°(等量代换)ABCDEF13243、如图,直线a∥b,点B在直线b上,且AB⊥BC,
∠1=55°,则∠2=
ABC2b1a4、如图AB∥CD,AD交BC于点O,∠A=500,
∠AOB=1000。求∠C的度数。ABCOD 作业布置必做题:教材第37页习题9.3第1、3题。
选做题:教材第37页习题9.3第4、5题。祝同学们学习进步谢谢大家!
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
