数学七年级下青岛版13.2多边形课件1

课件21张PPT。第二课时
多边形的内角和与外角和
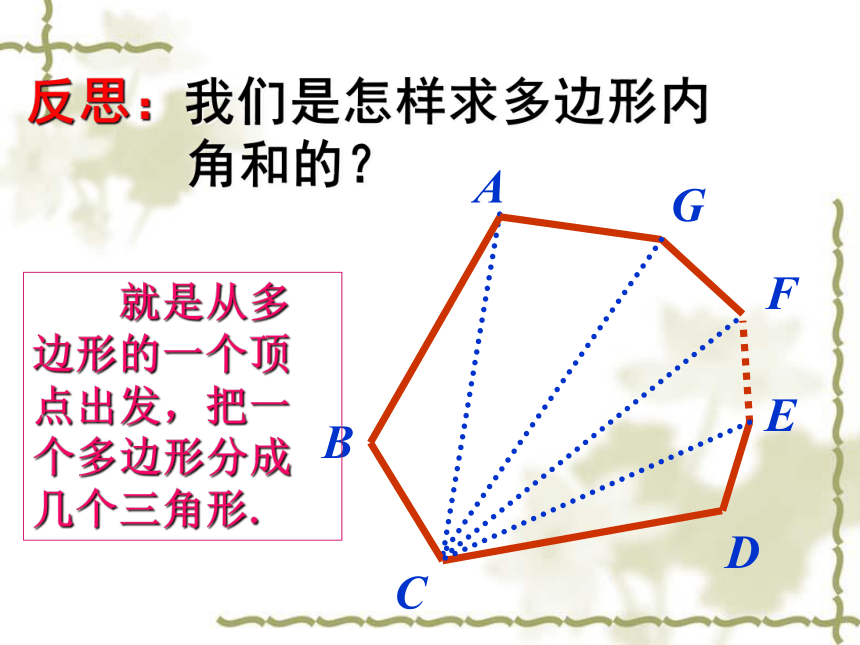
§13.2.2 多边形 B ACDE探究1五边形内角和=3×180°=540°………………34567n1n-22345180°360°540°720°900°(n－2) ·180°(n－2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°总结：n边形内角和公式n边形内角和=(n－2) ·180°反思：我们是怎样求多边形内
角和的？　　就是从多边形的一个顶点出发，把一个多边形分成几个三角形.E
ABCDO探究2180°× 5 – 360°= 540°180°× 5=900°？五边形内角和540°？？把一个五边形分成几个三角形，还有其他的分法吗？ABCDEF180° × 4 – 180° = 540°探究3探究4 A BCDE4 × 180°-180 °O=540°十二边形的内角和是（ ）。
一个多边形当边数增加1时，它的内角和增加（ ）。
一个多边形的内角和是720o，则此多边形共有（ ）个内角。
如果一个多边形的内角和是1440度，那么这是（ ）边形。1800o180o六十 例1 如图，在五边形的每个顶点处各取一个外角，这些外角的和叫做五边形的外角和．五边形的外角和等于多少？ 61.任意一个外角和他相邻的内角有什么关系？
2.五个外角加上他们分别相邻的五个内角和是多少？
3.这五个平角和与五边形的内角和、外角和有什么关系？ 例1 如图，在五边形的每个顶点处各取一个外角，这些外角的和叫做五边形的外角和．五边形的外角和等于多少？5边形外角和结论：五边形的外角和等于360°-(5-2) × 180°=360 °=5个平角-5边形内角和=5×180°探究在n边形的每个顶点处各取一个外角，这些外角的和叫做n边形的外角和．n边形外角和=结论：
n边形的外角和等于360°-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 °　　从多边形的一个顶点A点出发，沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向.在行程中所转的各个角的和，就是多边形的外角和.　　由于在这个运动过程中走了一周，也就是说所转的各个角的和等于一个周角.即：多边形的外角和等于360o练一练练习1：　　如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____.12n×30°=360°n=12n边形外角和=360 °练习2：正五边形的每一个外角等于____， 每一个内角等于_____。5x=360°x=72°72°144°解：设正五边形的每一个外角度数为x，由
多边形的外角和等于360度可得：所以每一个内角度数为108 °练习3. 已知一个多边形，它的内角和等 于外角和的2倍，求这个多边形的边数.解： 设多边形的边数为n
∵它的内角和等于 (n-2)?180°，
多边形外角和等于360o，
∴ (n-2)?180°=2× 360o。
解得: n=6
∴这个多边形的边数为6. 通过这节课的学习你有哪些收获？感悟与反思1.n边形的内角和等于__________，九 边形的内角和等于___________.
2.如果一个多边形的内角和是1440度，那么这是____边形。
3.已知多边形的每个内角都等于150°，求这个多边形的边数？
4.一个多边形从一个顶点可引对角线3条，这个多边形内角和等于（ ）
A.360° B.540° C.720° D.900°
5.已知一个多边形，它的内角和等于外角和的2倍，求这个多边形的边数？随堂练习 作　业P146习题13.2 第４、５、6题 再见