数学七年级下青岛版11.3单项式的乘法课件
文档属性
| 名称 | 数学七年级下青岛版11.3单项式的乘法课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 256.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-23 00:00:00 | ||
图片预览






文档简介
课件15张PPT。 第十一章11.3第2课时单项式乘多项式 单项式的乘法 单项式相乘,把它们的系数相乘、字母部分的同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。 1、如何进行单项式的乘法运算?想一想(系数×系数)×(同字母幂相乘)×单独的幂2. 什么叫多项式? 几个单项式的和叫做多项式。在多项式中,每个单项式叫做多项式的项。3. 什么叫多项式的项?说出多项式 2x2+3x-1的项和各项的系数计算1. ( 2a2b3c) (-3ab)2.==9= -6a3b4c新课引入2a.(3ka+1) =6ka2+2a
2a.(3ka+1) = 2a.3ka+2a
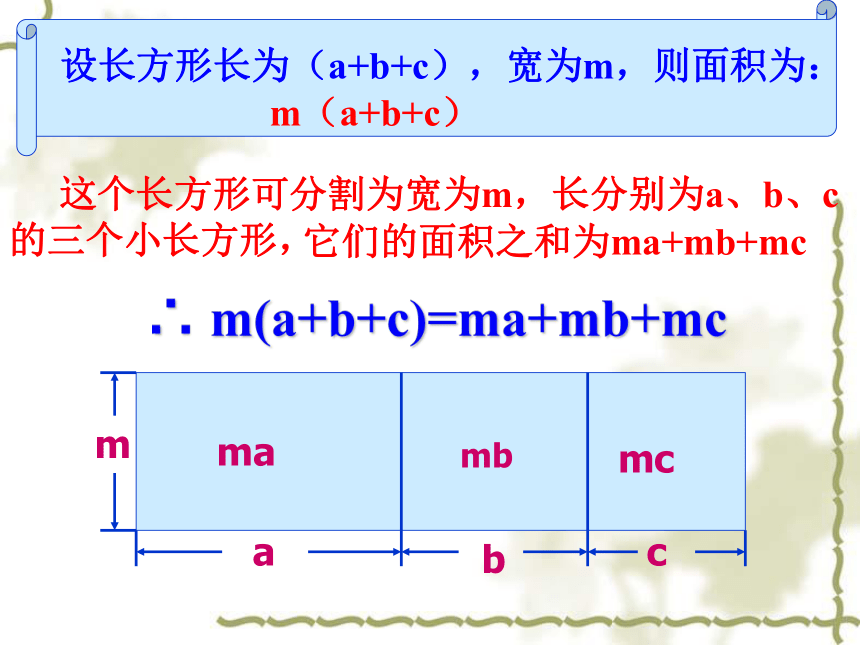
= 6ka2+2a 这个长方形可分割为宽为m,长分别为a、b、c的三个小长方形, ∴ m(a+b+c)=ma+mb+mcmabcmambmc它们的面积之和为ma+mb+mc设长方形长为(a+b+c),宽为m,则面积为:m(a+b+c)观察这两个式子有什么特征?思考:你能说出单项式与多项式相乘的法则吗?2a.(3ka+1) = 6ka2+2a
单项式与多项式相乘,先将单项式分别乘多项式的各项(每一项),再把所得的积相加。思路:单×多单×单典例分析例3 计算解:例4 化简解:单项式与多项式相乘时,分两个阶段:①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算。几点注意:1.单项式乘多项式的结果是多项式,
积的项数与原多项式的项数相同。 3.不要出现漏乘现象,运算要有顺序。2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:
同号相乘得正,异号相乘得负 做一做⑴、⑵、2、化简:1、计算:回顾交流:本节课我们学习了那些内容?单项式乘以多项式的依据是什么?如何进行单项式与多项式乘法运算? 求值问题,方法不是惟一
的,可以直接把字母的值代入
原式,但计算繁琐易出错,应
先化简,再代入求值,就显得
非常简捷。
探索与思考
2a.(3ka+1) = 2a.3ka+2a
= 6ka2+2a 这个长方形可分割为宽为m,长分别为a、b、c的三个小长方形, ∴ m(a+b+c)=ma+mb+mcmabcmambmc它们的面积之和为ma+mb+mc设长方形长为(a+b+c),宽为m,则面积为:m(a+b+c)观察这两个式子有什么特征?思考:你能说出单项式与多项式相乘的法则吗?2a.(3ka+1) = 6ka2+2a
单项式与多项式相乘,先将单项式分别乘多项式的各项(每一项),再把所得的积相加。思路:单×多单×单典例分析例3 计算解:例4 化简解:单项式与多项式相乘时,分两个阶段:①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算。几点注意:1.单项式乘多项式的结果是多项式,
积的项数与原多项式的项数相同。 3.不要出现漏乘现象,运算要有顺序。2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:
同号相乘得正,异号相乘得负 做一做⑴、⑵、2、化简:1、计算:回顾交流:本节课我们学习了那些内容?单项式乘以多项式的依据是什么?如何进行单项式与多项式乘法运算? 求值问题,方法不是惟一
的,可以直接把字母的值代入
原式,但计算繁琐易出错,应
先化简,再代入求值,就显得
非常简捷。
探索与思考
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
