数学七年级下青岛版13.1三角形课件4
文档属性
| 名称 | 数学七年级下青岛版13.1三角形课件4 |

|
|
| 格式 | zip | ||
| 文件大小 | 372.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-23 11:21:12 | ||
图片预览







文档简介
课件20张PPT。第四课时
三角形的内角与外角的关系
§15.1 三角形1.自主探索三角形的外角性质和外
角和.
2.掌握三角形的外角性质、外角和
及其应用. 学习目标:知识回顾1.三角形三个内角的和等于多少度?3.在△ABC中,
(1)∠C=90°,∠A=30 °,则∠B= ;
(2)∠A=50 °,∠B=∠C,则∠B= .
4.在△ABC中,
∠ A :∠ B :∠ C=2:3:4则
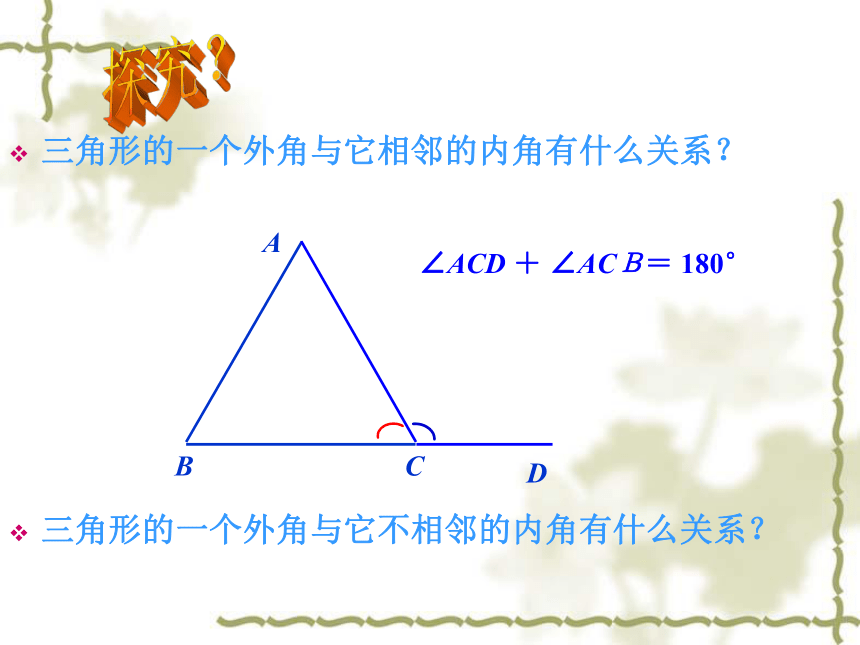
∠ A= ,∠ B= ,∠ C = .2.三角形的外角的意义?三角形的一个外角与它相邻的内角有什么关系?∠ACD + ∠ACB= 180°ABCD三角形的一个外角与它不相邻的内角有什么关系?探究?想一想, 填一填:∠ACD+∠1= °( )
又∵∠A+∠B+∠1= °( )
∴∠ACD ∠A+∠B.
180 平角的定义180=三角形的内角和是1800归纳:三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于任何一个与它不相邻的内角.学以致用:例1.如图,在△ABC中, BD是∠ABC的平分线,∠ABD=∠A,∠C=3∠A,求△ABC各个内角的度数.解:设∠A=x0,则∠ABC=2x0,∠C=3x0
由于三角形的内角和是1800,得x+2x+3x=180, 于是x=30,
从而∠A=300,∠ABC=600,∠C=900.学以致用:例2.如图,已知
∠ACD=1500, ∠A=2∠B,
求∠ B 的度数. 解:因为∠ACD是△ABC的一个外角,
所以∠ACD=∠A+∠B,
又因为∠A=2∠B于是∠ACD=2∠B+∠B=3∠B
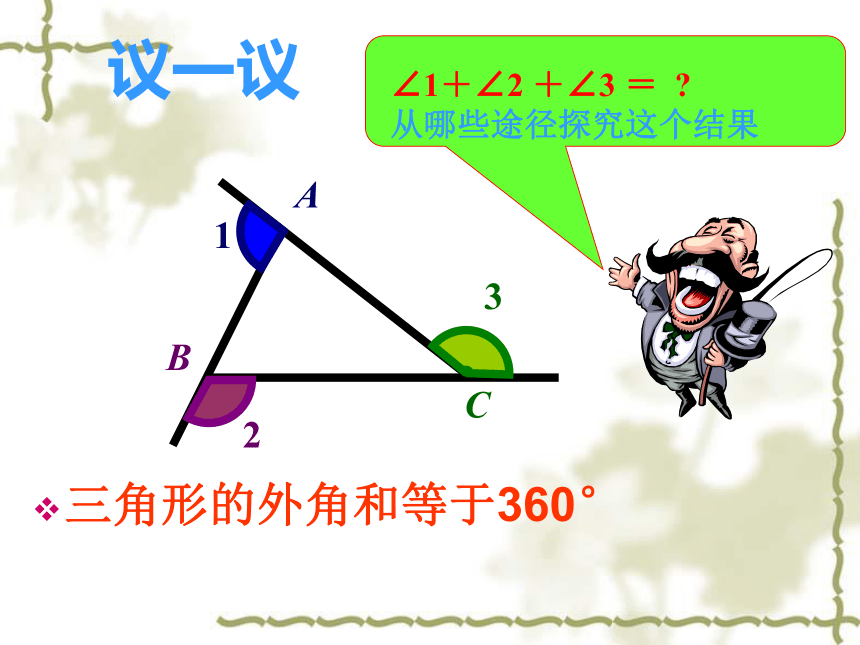
由∠ACD=1500,3∠B=1500 所以∠B=500三角形的外角和等于360° 议一议练一练:1.观察图形(1),回答问题:
(1)∠AED是?? ???? 的外角
∠ACD是??? ???? 的外角.
(2)∠AED =??? +?? ?,
∠ACD =?? ?? +? ?.
(3)∠AED > ? ???? .
∠ACD > ??? ???? .△CED△ACD∠ACD∠EDC∠CBA∠B∠ACD或∠EDC∠CAB或∠B练一练:2.如图,AB∥CD,
∠A=45°, ∠C=∠E,
求∠C的度数.
解:∵AB//CD,∠A=450, ∴∠DFE=∠450.
∵∠DFE是三角形的一个外角,∴∠DFE=∠E+∠C=450,
∴∠E=∠C , ∴∠C=22.50.3.等腰三角形的一个外角是1000,则它的顶角
的度数为( )
A.800 B.200 C.800或200 D. 500或800C练一练:4.如下图(1)∠A=310,∠D=410,
∠CFD=620,则∠B= .
5.如图(2)P是△ABC内的一点,延长BP
交AC于点D,用“<”表示∠1、∠2、∠A
的大小关系: 460∠1<∠2<∠A练一练:6.如图,求∠A+∠B+∠C+∠D+∠E的度数.解:∵∠1=∠A+∠C
∠2=∠B+∠E
又∵∠1+∠2+∠D=1800
∴∠A+∠B+∠C+∠D+∠E=1800ABCDE12达标测试:1.下列说法中,正确的是( ).
A.三角形的一个外角等于两个内角之和
B.三角形的一个外角大于任何一个内角
C.有一个外角是锐角的三角形是钝角三角形
D.有一个外角是钝角的三角形是锐角三角形。
2.在△ABC中,∠A=1150,∠B-∠C=50.则∠C的
度数为( ).
A.350 B.600 C.780 D.300
3.在△ABC中,∠A,∠B,∠C的外角的度数
比 是4:3:2,那么∠A=
CD1600细心做一做:4.如图,∠ABC=600,∠1=∠2.求∠3的
度数.解:∵∠ABC=∠2+∠4=600
∵∠1=∠2
∴∠1+∠4=600
∴∠3=∠1+∠4=6004动动笔头,实际应用: 一个零件的形状如图所示,按规定∠A应等于900 , ∠B 和∠C应分别是210和320,检验工人量得∠BDC=1480,就断定这个零件不合格.运用你学过的三角形的有关知识说明零件不合格的理由.
解:延长CD交AB于点E,
∵∠CEB=∠C+∠A,
∴∠CDB=∠CEB+∠B=
∠C+∠A+∠B=1430,
∵1480≠1430,∴不合理.连接中考: (北京市海淀区,2003)如图 ,把△ABC纸片沿
DE折叠,当点A落在四边形DEBC内部A′时, ∠A与
∠1+ ∠2之间存在着一种数量关系,试找出.解:由折叠知,
∠1+2∠EDA=1800
∠2+2∠DEA=1800
∴2(∠EDA+∠DEA)=1800-(∠1+∠2)
∵∠A+∠EDA+∠EDA=1800
∴∠A=900-1/2(∠1+∠2)通过这节课的学习你有什么收获?1.三角形的一个外角等于与它不相邻的两个
内角和.2.三角形的一个外角大于与它不相邻的任何
一个内角.3.三角形的外角和为360°.你说我说,清点收获 作业:习题A组第5、6题 谢
谢
光
临谢
谢
光
临
三角形的内角与外角的关系
§15.1 三角形1.自主探索三角形的外角性质和外
角和.
2.掌握三角形的外角性质、外角和
及其应用. 学习目标:知识回顾1.三角形三个内角的和等于多少度?3.在△ABC中,
(1)∠C=90°,∠A=30 °,则∠B= ;
(2)∠A=50 °,∠B=∠C,则∠B= .
4.在△ABC中,
∠ A :∠ B :∠ C=2:3:4则
∠ A= ,∠ B= ,∠ C = .2.三角形的外角的意义?三角形的一个外角与它相邻的内角有什么关系?∠ACD + ∠ACB= 180°ABCD三角形的一个外角与它不相邻的内角有什么关系?探究?想一想, 填一填:∠ACD+∠1= °( )
又∵∠A+∠B+∠1= °( )
∴∠ACD ∠A+∠B.
180 平角的定义180=三角形的内角和是1800归纳:三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于任何一个与它不相邻的内角.学以致用:例1.如图,在△ABC中, BD是∠ABC的平分线,∠ABD=∠A,∠C=3∠A,求△ABC各个内角的度数.解:设∠A=x0,则∠ABC=2x0,∠C=3x0
由于三角形的内角和是1800,得x+2x+3x=180, 于是x=30,
从而∠A=300,∠ABC=600,∠C=900.学以致用:例2.如图,已知
∠ACD=1500, ∠A=2∠B,
求∠ B 的度数. 解:因为∠ACD是△ABC的一个外角,
所以∠ACD=∠A+∠B,
又因为∠A=2∠B于是∠ACD=2∠B+∠B=3∠B
由∠ACD=1500,3∠B=1500 所以∠B=500三角形的外角和等于360° 议一议练一练:1.观察图形(1),回答问题:
(1)∠AED是?? ???? 的外角
∠ACD是??? ???? 的外角.
(2)∠AED =??? +?? ?,
∠ACD =?? ?? +? ?.
(3)∠AED > ? ???? .
∠ACD > ??? ???? .△CED△ACD∠ACD∠EDC∠CBA∠B∠ACD或∠EDC∠CAB或∠B练一练:2.如图,AB∥CD,
∠A=45°, ∠C=∠E,
求∠C的度数.
解:∵AB//CD,∠A=450, ∴∠DFE=∠450.
∵∠DFE是三角形的一个外角,∴∠DFE=∠E+∠C=450,
∴∠E=∠C , ∴∠C=22.50.3.等腰三角形的一个外角是1000,则它的顶角
的度数为( )
A.800 B.200 C.800或200 D. 500或800C练一练:4.如下图(1)∠A=310,∠D=410,
∠CFD=620,则∠B= .
5.如图(2)P是△ABC内的一点,延长BP
交AC于点D,用“<”表示∠1、∠2、∠A
的大小关系: 460∠1<∠2<∠A练一练:6.如图,求∠A+∠B+∠C+∠D+∠E的度数.解:∵∠1=∠A+∠C
∠2=∠B+∠E
又∵∠1+∠2+∠D=1800
∴∠A+∠B+∠C+∠D+∠E=1800ABCDE12达标测试:1.下列说法中,正确的是( ).
A.三角形的一个外角等于两个内角之和
B.三角形的一个外角大于任何一个内角
C.有一个外角是锐角的三角形是钝角三角形
D.有一个外角是钝角的三角形是锐角三角形。
2.在△ABC中,∠A=1150,∠B-∠C=50.则∠C的
度数为( ).
A.350 B.600 C.780 D.300
3.在△ABC中,∠A,∠B,∠C的外角的度数
比 是4:3:2,那么∠A=
CD1600细心做一做:4.如图,∠ABC=600,∠1=∠2.求∠3的
度数.解:∵∠ABC=∠2+∠4=600
∵∠1=∠2
∴∠1+∠4=600
∴∠3=∠1+∠4=6004动动笔头,实际应用: 一个零件的形状如图所示,按规定∠A应等于900 , ∠B 和∠C应分别是210和320,检验工人量得∠BDC=1480,就断定这个零件不合格.运用你学过的三角形的有关知识说明零件不合格的理由.
解:延长CD交AB于点E,
∵∠CEB=∠C+∠A,
∴∠CDB=∠CEB+∠B=
∠C+∠A+∠B=1430,
∵1480≠1430,∴不合理.连接中考: (北京市海淀区,2003)如图 ,把△ABC纸片沿
DE折叠,当点A落在四边形DEBC内部A′时, ∠A与
∠1+ ∠2之间存在着一种数量关系,试找出.解:由折叠知,
∠1+2∠EDA=1800
∠2+2∠DEA=1800
∴2(∠EDA+∠DEA)=1800-(∠1+∠2)
∵∠A+∠EDA+∠EDA=1800
∴∠A=900-1/2(∠1+∠2)通过这节课的学习你有什么收获?1.三角形的一个外角等于与它不相邻的两个
内角和.2.三角形的一个外角大于与它不相邻的任何
一个内角.3.三角形的外角和为360°.你说我说,清点收获 作业:习题A组第5、6题 谢
谢
光
临谢
谢
光
临
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
