5.7 三角函数的应用 学案(含答案)
文档属性
| 名称 | 5.7 三角函数的应用 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 367.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 00:00:00 | ||
图片预览



文档简介
第五章 三角函数
5.7 三角函数的应用
学案
学习目标
1.会用三角函数解决一些简单的实际问题.
2.体会可以利用三角函数构建刻画事物周期变化的数学模型.
知识汇总
在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的运动称为“简谐运动”.在适当的直角坐标系下,简谐运动可以用函数,表示,其中,.
(1)振幅:A就是这个简谐运动的振幅,它是做简谐运动的物体离开平衡位置的最大位置.
(2)周期:,它是做简谐运动的物体往复运动一次所需要的时间.
(3)频率:,它是做简谐运动的物体在单位时间内往复运动的次数.
(4)相位:;时的相位称为初相.
习题检测
1.已知某人的血压满足函数解析式,其中为血压(单位:mmHg),t为时间(单位:min),则此人每分钟心跳的次数为( )
A.60 B.70 C.80 D.90
2.音叉是呈“Y”型的钢质或铝合金发声器(如图1),各种音叉可因其质量和叉臂长短、粗细不同而在振动时发出不同频率的纯音.敲击某个音叉时,在一定时间内,音叉上点P离开平衡位置的位移y与时间t的函数关系为.图2是该函数在一个周期内的图象,根据图中数据可确定的值为( )
A.200 B.400 C. D.
3.如图所示的是一个单摆,以平衡位置OA为始边、OB为终边的角与时间t(s)满足函数关系式,则当时,角的大小,单摆的频率分别是( )
A., B.2, C., D.2,
4.商场人流量被定义为每分钟通过入口的人数,五一某商场的人流量满足函数,则下列时间段内人流量是增加的是( )
A. B. C. D.
5.电流强度I(安培)随时间t(秒)变化的函数的图象如图所示,则时的电流强度为( )
A.0安培 B.安培 C.安培 D.安培
6.如图表示电流强度I与时间t的关系在一个周期内的图象,则该函数解析式可以是( )
A. B.
C. D.
7.在两个弹簧上各有一个小球做上下自由振动,它们的质量分别为和.已知它们在时间离开平衡位置的位移和分别由和确定,则当时,与的大小关系是( )
A. B. C. D.不能确定
8.已知某简谐运动的振幅是,,图象上相邻最高点和最低点的距离是5,且过点,则该简谐运动的频率和初相是( )
A. B. C. D.
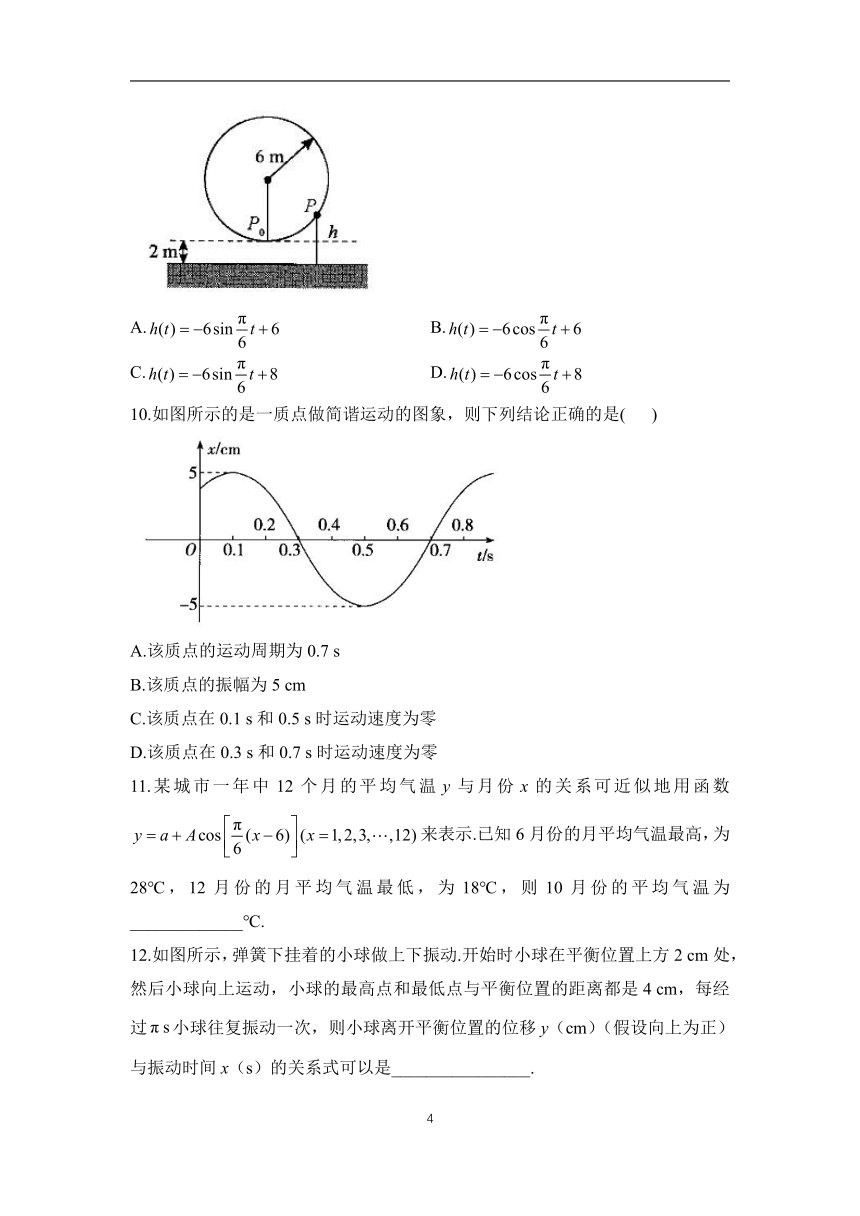
9.如图,一个大风车的半径为6m,12min旋转一周,它的最低点离地面2m,风车翼片的一个端点P从开始按逆时针方向旋转,则点P离地面距离h(m)与时间t(min)之间的函数关系式是( )
A. B.
C. D.
10.如图所示的是一质点做简谐运动的图象,则下列结论正确的是( )
A.该质点的运动周期为0.7 s
B.该质点的振幅为5 cm
C.该质点在0.1 s和0.5 s时运动速度为零
D.该质点在0.3 s和0.7 s时运动速度为零
11.某城市一年中12个月的平均气温y与月份x的关系可近似地用函数来表示.已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温为_____________℃.
12.如图所示,弹簧下挂着的小球做上下振动.开始时小球在平衡位置上方2 cm处,然后小球向上运动,小球的最高点和最低点与平衡位置的距离都是4 cm,每经过小球往复振动一次,则小球离开平衡位置的位移y(cm)(假设向上为正)与振动时间x(s)的关系式可以是________________.
13.如图是一个缆车示意图,该缆车的半径为4.8 m,圆上最低点与地面的距离为0.8 m,缆车每60 s转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动角到OB,设B点与地面的距离为h m.
(1)求h与之间的函数解析式;
(2)设从OA开始转动,经过t s达到OB,求h与t之间的函数解析式,并计算经过45 s后缆车距离地面的高度.
答案以及解析
1.答案:C
解析:由函数解析式易知周期为,故频率即为每分钟心跳的次数,为80.
2.答案:D
解析:由题图可得,,,即,则.故选D.
3.答案:A
解析:当时,,由函数解析式易知单摆的周期为,故单摆的频率为.
4.答案:C
解析:由,,得,,所以函数的增区间为,.当时,,而,故选C.
5.答案:A
解析:由题图知,函数的周期,所以,则,将点代入,可得,,.又,,故函数解析式为,将代入函数解析式,得.
6.答案:C
解析:由题图得,,
,.
又函数图象过点,则,,
取,.
7.答案:C
解析:当时,;
当时,,故.
8.答案:C
解析:设该简谐运动的最小正周期为T,由题意可知,,则,则.将点代人,得,即,,.该简谐运动的频率是,初相是.
9.答案:D
解析:设.∵12min旋转一周,,.最大值与最小值分别为14,2,解得..故选D.
10.答案:BC
解析:由题图可知,运动周期为,故A错误;该质点的振幅为5 cm,B正确;由简谐运动的特点知,质点在0.3 s和0.7 s时运动速度最大,在0.1 s和0.5 s时运动速度为零,故C正确,D错误.故选BC.
11.答案:20.5
解析:当时,;当时,.解得,.所以当时,.
12.答案:(答案不唯一)
解析:不妨设(其中,).由题知,,所以.当时,,且小球开始向上运动,所以,,不妨取,故所求关系式可以为.
13.答案:(1)以圆心O为原点,建立如图所示的平面直角坐标系,
则以Ox为始边,OB为终边的角为,
故点B的坐标为,
.
(2)易知点A在圆上转动的角速度是,
故t s转过的弧度数为,
,.
当时,.
即经过45 s后缆车距离地面的高度为5.6 m.
2
5.7 三角函数的应用
学案
学习目标
1.会用三角函数解决一些简单的实际问题.
2.体会可以利用三角函数构建刻画事物周期变化的数学模型.
知识汇总
在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的运动称为“简谐运动”.在适当的直角坐标系下,简谐运动可以用函数,表示,其中,.
(1)振幅:A就是这个简谐运动的振幅,它是做简谐运动的物体离开平衡位置的最大位置.
(2)周期:,它是做简谐运动的物体往复运动一次所需要的时间.
(3)频率:,它是做简谐运动的物体在单位时间内往复运动的次数.
(4)相位:;时的相位称为初相.
习题检测
1.已知某人的血压满足函数解析式,其中为血压(单位:mmHg),t为时间(单位:min),则此人每分钟心跳的次数为( )
A.60 B.70 C.80 D.90
2.音叉是呈“Y”型的钢质或铝合金发声器(如图1),各种音叉可因其质量和叉臂长短、粗细不同而在振动时发出不同频率的纯音.敲击某个音叉时,在一定时间内,音叉上点P离开平衡位置的位移y与时间t的函数关系为.图2是该函数在一个周期内的图象,根据图中数据可确定的值为( )
A.200 B.400 C. D.
3.如图所示的是一个单摆,以平衡位置OA为始边、OB为终边的角与时间t(s)满足函数关系式,则当时,角的大小,单摆的频率分别是( )
A., B.2, C., D.2,
4.商场人流量被定义为每分钟通过入口的人数,五一某商场的人流量满足函数,则下列时间段内人流量是增加的是( )
A. B. C. D.
5.电流强度I(安培)随时间t(秒)变化的函数的图象如图所示,则时的电流强度为( )
A.0安培 B.安培 C.安培 D.安培
6.如图表示电流强度I与时间t的关系在一个周期内的图象,则该函数解析式可以是( )
A. B.
C. D.
7.在两个弹簧上各有一个小球做上下自由振动,它们的质量分别为和.已知它们在时间离开平衡位置的位移和分别由和确定,则当时,与的大小关系是( )
A. B. C. D.不能确定
8.已知某简谐运动的振幅是,,图象上相邻最高点和最低点的距离是5,且过点,则该简谐运动的频率和初相是( )
A. B. C. D.
9.如图,一个大风车的半径为6m,12min旋转一周,它的最低点离地面2m,风车翼片的一个端点P从开始按逆时针方向旋转,则点P离地面距离h(m)与时间t(min)之间的函数关系式是( )
A. B.
C. D.
10.如图所示的是一质点做简谐运动的图象,则下列结论正确的是( )
A.该质点的运动周期为0.7 s
B.该质点的振幅为5 cm
C.该质点在0.1 s和0.5 s时运动速度为零
D.该质点在0.3 s和0.7 s时运动速度为零
11.某城市一年中12个月的平均气温y与月份x的关系可近似地用函数来表示.已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温为_____________℃.
12.如图所示,弹簧下挂着的小球做上下振动.开始时小球在平衡位置上方2 cm处,然后小球向上运动,小球的最高点和最低点与平衡位置的距离都是4 cm,每经过小球往复振动一次,则小球离开平衡位置的位移y(cm)(假设向上为正)与振动时间x(s)的关系式可以是________________.
13.如图是一个缆车示意图,该缆车的半径为4.8 m,圆上最低点与地面的距离为0.8 m,缆车每60 s转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动角到OB,设B点与地面的距离为h m.
(1)求h与之间的函数解析式;
(2)设从OA开始转动,经过t s达到OB,求h与t之间的函数解析式,并计算经过45 s后缆车距离地面的高度.
答案以及解析
1.答案:C
解析:由函数解析式易知周期为,故频率即为每分钟心跳的次数,为80.
2.答案:D
解析:由题图可得,,,即,则.故选D.
3.答案:A
解析:当时,,由函数解析式易知单摆的周期为,故单摆的频率为.
4.答案:C
解析:由,,得,,所以函数的增区间为,.当时,,而,故选C.
5.答案:A
解析:由题图知,函数的周期,所以,则,将点代入,可得,,.又,,故函数解析式为,将代入函数解析式,得.
6.答案:C
解析:由题图得,,
,.
又函数图象过点,则,,
取,.
7.答案:C
解析:当时,;
当时,,故.
8.答案:C
解析:设该简谐运动的最小正周期为T,由题意可知,,则,则.将点代人,得,即,,.该简谐运动的频率是,初相是.
9.答案:D
解析:设.∵12min旋转一周,,.最大值与最小值分别为14,2,解得..故选D.
10.答案:BC
解析:由题图可知,运动周期为,故A错误;该质点的振幅为5 cm,B正确;由简谐运动的特点知,质点在0.3 s和0.7 s时运动速度最大,在0.1 s和0.5 s时运动速度为零,故C正确,D错误.故选BC.
11.答案:20.5
解析:当时,;当时,.解得,.所以当时,.
12.答案:(答案不唯一)
解析:不妨设(其中,).由题知,,所以.当时,,且小球开始向上运动,所以,,不妨取,故所求关系式可以为.
13.答案:(1)以圆心O为原点,建立如图所示的平面直角坐标系,
则以Ox为始边,OB为终边的角为,
故点B的坐标为,
.
(2)易知点A在圆上转动的角速度是,
故t s转过的弧度数为,
,.
当时,.
即经过45 s后缆车距离地面的高度为5.6 m.
2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
