同底数幂的乘法课件

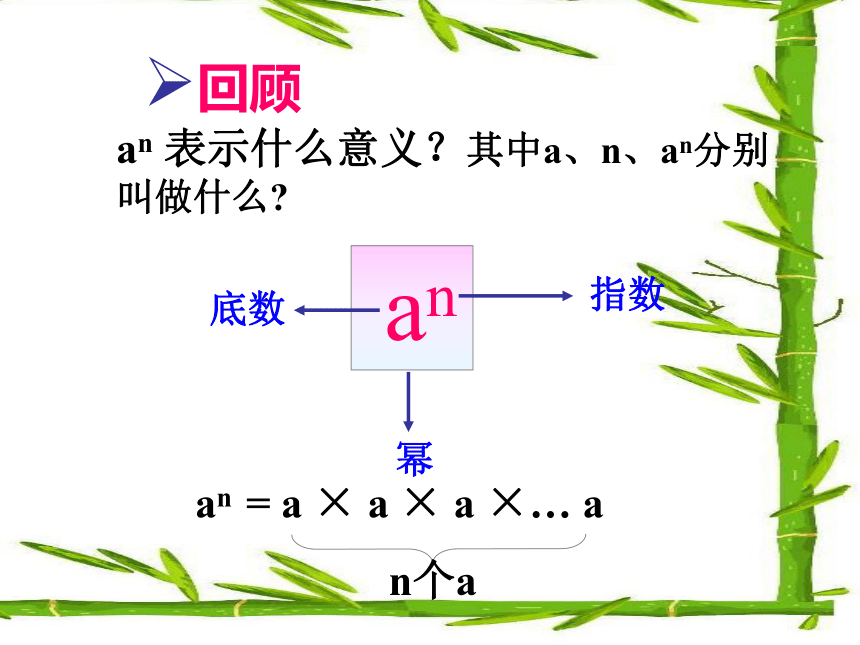
课件26张PPT。人教实验版同底数幂的乘法an 表示什么意义？其中a、n、an分别叫做什么? an底数幂指数回顾an = a × a × a ×… a
n个a
八年级 数学1.什么叫乘方？-22aa+12425求几个相同因数的积的运算叫做乘方。 105 = .
?
10×10×10×10×10104 10×10×10×10= .(乘方的意义）问题： 105表示什么？
10×10×10×10可以写成什么形式?
(乘方的意义）八年级 数学
102 ×104 = （ 10 × 10 ） × （10× 10 × 10 × 10 ）
= 10 （ ） ；
104 × 105 = .
= 10（ ） ；
103× 105 = .
= 10（ ） 根据乘方的意义，解答下列各题.（10×10 ×10 ×10 )×( 10× 10 × 10 ×10× 10 )（10×10 ×10 )×( 10× 10 × 10 ×10× 10 )698八年级 数学尝试探讨,学习新知m个10n个10= 10× 10×… ×10=10m+n(m+n)个10（10× 10× … × 10）（ 10× 10×… ×10） 如何计算10m× 10n(m,n为正整数）？ 10m× 10n=八年级 数学尝试探讨,学习新知探究
25 ×22 = 2（ ） ；
a3 ·a2 = a（ ） ；
5m·5n = 5（ ） 75m+n 2m× 2n等于什么？
（ ）m× （ ）n 呢（ m,n为正整数） ？ 2m+n八年级 数学尝试探讨,学习新知八年级 数学 am · an =m个an个a= aa…a=am+n(m+n)个a（aa…a）（aa…a）am+n（乘法结合律）（乘方的意义）am · an= (m、n为正整数)（乘方的意义）尝试探讨,学习新知am · an = am+n (m、n为正整数)同底数幂的乘法性质： 如 am·an·ap = am+n+p （m、n、p都是正整数）观察am · an = am+n (m、n为正整数)，此式子的左边与右边的底数和指数，各有什么特点？想一想： 当三个或三个以上同底数幂相乘时，是否也 　? 具有这一性质呢？八年级 数学第十五章整式的乘除与因式分解15.1整式的乘法例１ 计算：
(1) x2·x5; (2) a·a6; (3) 2×24×23; (4) xm·x3m+1.解： (1)x2·x5 =x2+5 =x 7. (4) xm·x3m+1=xm+3m+1 = x 4m+1.(3)2×24×23=21+4+3=28.(2) a·a6 =a1+6 =a7.例1.计算： （1）(－8)12 × (－8)3 ； （2）x · x7 . 解：（1） 原式 = (－8)12 + 3=－815（2）原式 = x1 +7 = x8(3)( — )5·(— )6·( — )=(－8)15八年级 数学例1.计算： （4） － a3 · a6 ； （5） x · x 2·x 3解：（4） 原式 = －a3 + 6（7）原式 = x3m +2m—1（6）(x+y)2· (x+y)3 (7) x3m · x2m—1（m为正整数）
（5）原式 = x1 +2+3（6）原式 = (x+y)2+3= x5m—1= (x+y)5= x6=－a9八年级 数学
(1) x3·x4 + x3·x3·x
(2) 2xn·xn-1 +(—x)3·(—x)2n-4??(2) 原式=2x2n-1+(-x)2n-1解:（1）原式=x7+x7=x2n-1=2x2n-1-x2n-1 =2x7(3) 23×4×8 ×16（结果用幂的形式表示.）(3) 原式=23×22 × 23 × 24= 23+2+3+4= 212例2：计算
八年级 数学路程：时间:5 × 10 2 s
= 15×1010
= 1.5 ×1011 练习一
(1011 )( a11 )（ —x6）（ —223 ）（2） a8 ·a3（3） —x5 ·x （4） （—2）10× （—2）13（1） 105×106（5） y4·y3·y2·y （ y10 ）（6） x4·x6+x5·x5 （7） a·a7—a4·a4 （ 2 x10 ）（ 0 ）八年级 数学1.???计算：（口答）2、 判断题：
（1）a2 ·a3= a6（ ）（2）a2 + a2 = a 4（ ）
（3）xm ·xm = 2xm ( ) （4） 2xm +xm = 3xm ( )
（5）c · c3 = c3 ( ) （6）3m +2 m = 5m ( )
× × ××× √练习一
八年级 数学
在幂的运算中，经常会用到如下一些变形：
(1)(-a)2=a2,(-a)4=a4,(-a)6=a6……
(2)(-a)3= —a3,(-a)5= —a5,(-a)7=—a7……
(3)(b-a)2=(a-b)2,(b-a)4=(a-b)4……
(4)(b-a)3= —(a-b)3,(b-a)5= —(a-b)5……说明：八年级 数学典型例题解析1、计算（结果用幂的形式）
（1）—(－a)３ · (－a)２ · a5 （2）(a－b)3 · (b－a)2（3）－8× (－2)6八年级 数学(a-b)5 a10 -29 (1) x8=x( ) ·x5(2) (a+b)n+2=(a+b)n ·(a+b)( )(3) y 3m=y2m· ( )(4) x7= x · （ ） = x3 · （ ）思维拓展训练八年级 数学逆用法则2填空：32ymx6x42、若xm =3, xn =2,则xm+n=(? ?)????
A. 5??? ?B. 6?? ??C.—5? ???D.—6B1、y2m+2 可写成(? ?)
??A. 2ym+1???B. y2m· y2???C.y2· ym+1????D.y2m+ y2B思维拓展训练选择题：八年级 数学 选择题：AB3.若x、y是正整数,且2x·2y=25,则x、y的值有（?? ）????
A. 4对????B. 3对????C. 2 对????D. 1对4.已知 22× 8 = 2n, 则 n 的 值为（?? ）????
A.4 ???? B.5?? ? ?C.6??? D.7思维拓展训练八年级 数学 选择题：C思维拓展训练 xn 与(-x)n 的正确关系是（ ??）??
A.相等 B.互为相反数
C.当n为奇数时，它们互为相反数；当n为偶数时，
它们相等.
D.当n为奇数时，它们相等；当n为偶数时，它们
互为相反数.八年级 数学小结我学到了什么？ 知识　 　　方法　同底数幂相乘，　
底数　　 指数　
am · an = am+n (m、n正整数)　“特殊→一般→特殊”
　 例子 公式 应用相加.不变，八年级 数学八年级 数学15.1整式的乘法阅读下面的解题过程试比较2100与375的大小。请根据上述解答，比较3100与560的大小解：因为2100=（24）25，375=（33）25又24=16，33=27，且16＜ 27，所以2100 ＜375，比较3555、4444、5333的大小，解：∵3555＝35×111＝(35)111＝243111，
4444＝44×111＝(44)111＝256111，
5333＝53×111＝(53)111＝125111，
又256＞243＞125，
∴ 5333＜3555＜4444思考题八年级 数学