第四章 指数函数与对数函数 单元综合练习卷(含答案)
文档属性
| 名称 | 第四章 指数函数与对数函数 单元综合练习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 97.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 14:02:20 | ||
图片预览



文档简介
第四章 指数函数与对数函数单元综合练习卷
一.选择题(共8小题)
1.里氏震级(M)是表示地震规模大小的标度,它是由观测点处地震仪所记录到的地震波最大振幅(A)和观测点所在地规模0地震所应有的振幅(A0)的常用对数演算而来的,其计算公式为.2023年8月6日2时33分,山东省德州市平原县发生5.5级地震,29分钟后又发生3.0级地震,用A5.5和A3.0分别表示震级为5.5和3.0的地震波最大振幅,则=( )(参考数据:)
A.25 B.31.6 C.250 D.316
2.2022年诺贝尔物理学奖授予在量子领域做出贡献的法国、美国、奥地利科学家,我国于2021年成功研制出目前国际上超导量子比特数量最多的量子计算原型机“祖冲之号”,操控的超导量子比特为66个.已知1个超导量子比特共有“|0>,|1>”2种叠加态,2个超导量子比特共有“|00>,|01>,|10>,|11>”4种叠加态,3个超导量子比特共有“|000>,|001>,|010>,|011>,|100>,|101>,|110>,|111>”8种叠加态,…,只要增加1个超导量子比特,其叠加态的种数就呈指数级增长.设M个超导量子比特共有N种叠加态,且N是一个20位的数,则这样的M有( )个.(参考数据:lg2≈0.3010)
A.2 B.3 C.4 D.5
3.若二次函数y1=x2﹣ax+b的两个零点为2,3,则二次函数y2=bx2﹣ax﹣1的零点是( )
A.﹣1, B.1,﹣ C., D.﹣,﹣
4.某地投资a亿元进行基础建设,t年后产生的社会经济效益为f(t)=aeλt亿元,若该地投资基础建设4年后产生的社会经济效益是投资额的2倍,且再过t1年,该项投资产生的社会经济效益是投资额的16倍,则t1=( )
A.4 B.8 C.12 D.16
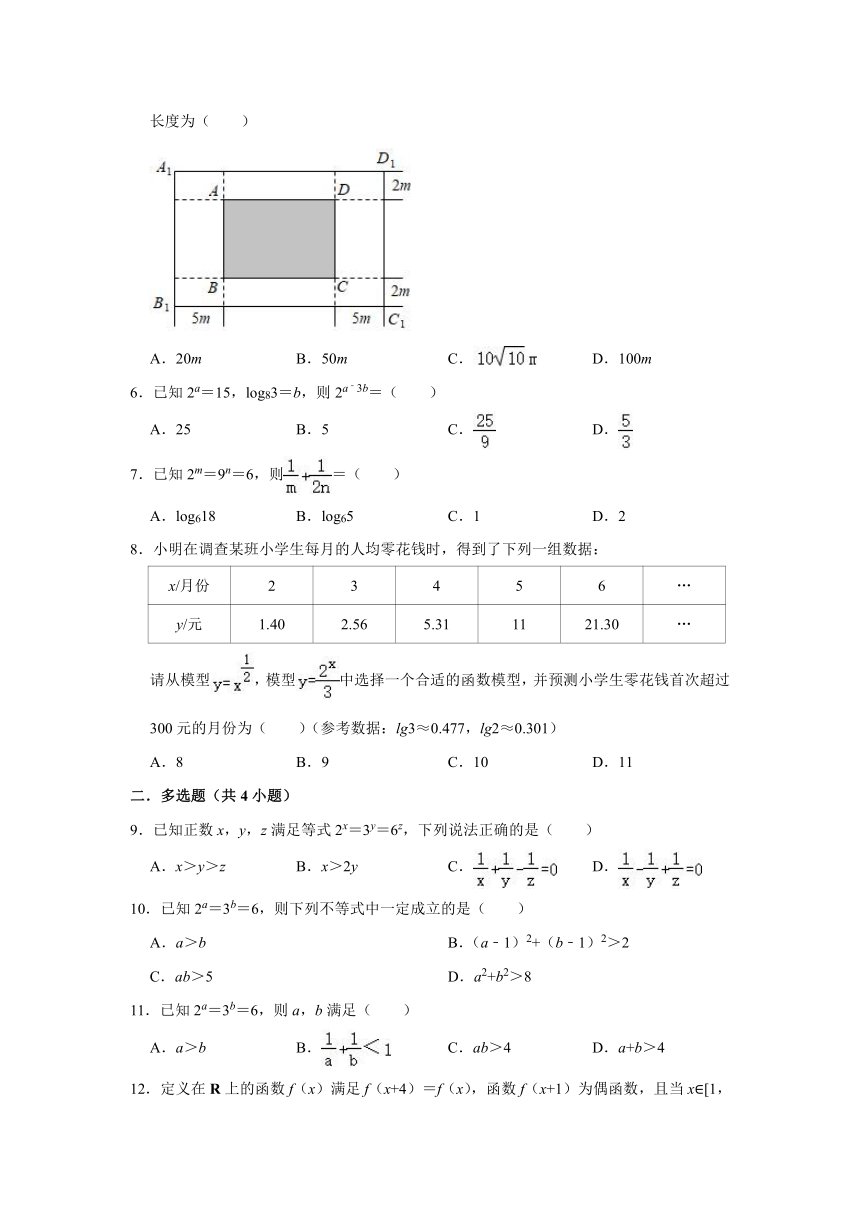
5.为了不断满足人民日益增长的美好生活需要,实现群众对舒适的居住条件、更优美的环境、更丰富的精神文化生活的追求,某大型广场正计划进行升级改造.改造的重点工程之一是新建一个长方形音乐喷泉综合体A1B1C1D1,该项目由长方形核心喷泉区ABCD(阴影部分)和四周绿化带组成.规划核心喷泉区的ABCD面积为1000m2,绿化带的宽分别为2m和5m(如图所示).当整个项目占地面积A1B1C1D1最小时,则核心喷泉区BC的长度为( )
A.20m B.50m C. D.100m
6.已知2a=15,log83=b,则2a﹣3b=( )
A.25 B.5 C. D.
7.已知2m=9n=6,则=( )
A.log618 B.log65 C.1 D.2
8.小明在调查某班小学生每月的人均零花钱时,得到了下列一组数据:
x/月份 2 3 4 5 6 …
y/元 1.40 2.56 5.31 11 21.30 …
请从模型,模型中选择一个合适的函数模型,并预测小学生零花钱首次超过300元的月份为( )(参考数据:lg3≈0.477,lg2≈0.301)
A.8 B.9 C.10 D.11
二.多选题(共4小题)
9.已知正数x,y,z满足等式2x=3y=6z,下列说法正确的是( )
A.x>y>z B.x>2y C. D.
10.已知2a=3b=6,则下列不等式中一定成立的是( )
A.a>b B.(a﹣1)2+(b﹣1)2>2
C.ab>5 D.a2+b2>8
11.已知2a=3b=6,则a,b满足( )
A.a>b B. C.ab>4 D.a+b>4
12.定义在R上的函数f(x)满足f(x+4)=f(x),函数f(x+1)为偶函数,且当x∈[1,3]时,f(x)=﹣x2+2x,则( )
A.f(x)的图象关于点(2,0)成中心对称
B.对任意整数k,f(2k)=0
C.f(x)的值域为[﹣3,1]
D.3f(x)﹣x+2=0的实数根个数为7
三.填空题(共4小题)
13.牛顿曾经提出了常温环境下的温度冷却模型:,其中t为时间(单位:min),θ0为环境温度,θ1为物体初始温度,θ为冷却后温度.假设在室内温度为20℃的情况下,一杯饮料由100℃降低到60℃需要20min,则此饮料从60℃降低到25℃需要 min.
14.已知函数f(x)=logax(a>0且a≠1)在区间上的最大值是2,则a= .
15.已知函数,若函数g(x)=f(x)﹣a有两个零点,则实数a的取值范围是 .
16.已知函数若方程f(x)=m有四个不同的实根x1,x2,x3,x4,满足x1<x2<x3<x4,则的取值范围是 .
四.解答题(共6小题)
17.化简求值:
(1);
(2).
18.已知x1,x2是方程x2﹣6x+k=0的两个实数根,且x12 x22﹣x1﹣x2=115.
(1)求k的取值.
(2)求x12+x22﹣8的值.
19.新学期开学季,成都某学校附近又新开了一家奶茶店,其中有一种名为“奶茶三兄弟”的饮品很受学生欢迎,老板费尽心思想在这种饮品上赚得第一桶金,其销售的价格在一学期不同周次有所变化.设开始时每杯定价10元,从第一次周开始每周涨价2元,5周后开始保持20元的价格平稳销售,10周后,学生的新鲜感已过,平均每周削价2元,直到16周周末,老板为了让学生安心准备期末考试复习而不挂念“三兄弟”,该饮品暂停销售.
(1)试求该饮品每杯价格p(元)与周次t,(t∈[1,16],t∈N)之间的函数关系式;
(2)若此饮品每杯成本价q(元)与周次t之间的关系是(t﹣8)2+12,t∈[1,16],t∈N,试问该饮品第几周每杯的销售利润最大,并求出最大值.
20.某种植户要倚靠院墙建一个高3m的长方体温室用于育苗,至多有54m2的材料可用于3面墙壁和顶棚的搭建,设温室中墙的边长分别为x,y,如图所示.
(1)写出:x,y满足的关系式;
(2)求温室体积的最大值.
21.已知函数y=ax2﹣(a+2)x+2,a∈R
(1)y<3﹣2x恒成立,求实数a的取值范围;
(2)若存在m>0使关于x的方程有四个不同的实根,求实数a的取值.
22.已知函数,函数,
(Ⅰ)已知直线l是曲线y=f(x)在点(0,f(0))处的切线,且l与曲线y=g(x)相切,求a的值;
(Ⅱ)若方程f(x)=g(x)有三个不同实数解,求实数a的取值范围.
参考答案
一.选择题(共8小题)
1--8DBBCB BCC
二.多选题(共4小题)
9.AC
10.ABD
11.ACD
12.BCD
三.填空题(共4小题)
13.60
14. 或4
15.[﹣1,0] {1}
16.(10,12)
四.解答题(共6小题)
17.解:(1)原式=
=;
(2)原式=
=4+2lg2+2lg2×lg5+2(lg5)2=4+2lg2+2lg5(lg2+lg5)
=4+2lg2+2lg5=4+2=6.
18.解:(1)由题意可得,x1+x2=6,x1x2=k,Δ=36﹣4k≥0,
所以k≤9,
∵x12 x22﹣x1﹣x2=k2﹣6=115,
所以k=11(舍)或k=﹣11,
(2)x12+x22﹣8==36+22﹣8=50.
19.解:(1)由题意得当0≤t≤5且t∈N*时,p=10+2t;
当5<t≤10且t∈N*时,p=20;
当10<t≤16且t∈N*时,p=40﹣2t,
综上所述,p=;
(2)由(1)得p=,(t﹣8)2+12,t∈[1,16],t∈N,
设利润为W,则W=p﹣q,
∴当0≤t≤5且t∈N*时,,W=10+2t﹣[﹣(t﹣8)2+12]=t2+6,
∴当t=5时,Wmax=9.125;
当5<t≤10且t∈N*时,W=20﹣[﹣(t﹣8)2+12]=t2﹣2t+16,
∴当t=8时,Wmax=8;
当10<t≤16且t∈N*时,W=40﹣2t﹣[﹣(t﹣8)2+12=t2﹣4t+36,
∴当t=11时,Wmax=7.125,
∵9.125>8>7.125,
∴该饮品第5周每杯的销售利润最大,且最大值9.125元.
20.解:(1)由题意得,顶棚所用材料的面积为xy,3面墙壁所用材料的面积为3x+6y,
∵至多有54m2的材料可用于3面墙壁和顶棚的搭建,
∴xy+3x+6y≤54(0<x<18,0<y<9).
(2)∵3x+6y≥2=6,
当且仅当x=2y时取等号,
∴xy+6≤xy+3x+6y≤54,
令=t>0,则t2+6t﹣54≤0,
解得0<t≤3,即0<xy≤18,
当且仅当x=6,y=3时取等号,
∴温室体积V=3xy≤54,
则温室体积的最大值为54m3.
21.解:(1)由题有ax2﹣(a+2)x+2<3﹣2x恒成立,
即ax2﹣ax﹣1<0恒成立,
当a=0时,﹣1<0恒成立,符合题意,
当a≠0时,则,得,
得﹣4<a<0,
综上,a的取值范围为(﹣4,0].
(2)当m>0时,令t=m++1≥2+1=3,
当且仅当m=1时取等号,
则关于x的方程f(|x|)=t可化为a|x|2﹣(a+2)|x|+2﹣t=0,
关于x的方程为a|x|2﹣(a+2)|x|+2﹣t=0有四个不等的实数根,
即ax2﹣(a+2)x+2﹣t=0,有两个不同的实数正根,
则,解得a<﹣2,
由(1)可知存在t∈[3,+∞)使得不等式4at+(a+2)2﹣8a>0成立,
故4a×3+(a+2)2﹣8a>0,即a2+8a+4>0,
解得a<﹣4﹣2或a>﹣4+2,
综上可得a<﹣4﹣2,
所以a的取值范围为(﹣∞,﹣4﹣2).
22.解:(Ⅰ)∵函数f(x)=x3﹣6x的导数为f′(x)=x2﹣6,
∴曲线y=f(x)在点(0,f(0))处的切线l的方程为y=﹣6x,
又曲线g(x)=上点(m,n)为切点的切线l的方程为,
∴,解得a=18.
(Ⅱ)记F(x)=f(x)﹣g(x)=x3﹣x2﹣6x﹣a,
F′(x)=x2﹣x﹣6,由F′(x)=0,可得x=﹣2或x=3.
当x<﹣2时,F′(x)>0,F(x)递增;
当﹣2<x<3时,F′(x)<0,F(x)递减;
当x>3时,F′(x)>0,F(x)递增.
可得x=﹣2时,F(x)取得极大值,且为﹣a,
x=3时,F(x)取得极小值,且为﹣a,
因为当x→+∞,F(x)→+∞;x→﹣∞,F(x)→﹣∞.
则方程f(x)=g(x)有三个不同实数解的等价条件为:
﹣a>0且﹣a<0,解得<a<.
故实数a的取值范围为
一.选择题(共8小题)
1.里氏震级(M)是表示地震规模大小的标度,它是由观测点处地震仪所记录到的地震波最大振幅(A)和观测点所在地规模0地震所应有的振幅(A0)的常用对数演算而来的,其计算公式为.2023年8月6日2时33分,山东省德州市平原县发生5.5级地震,29分钟后又发生3.0级地震,用A5.5和A3.0分别表示震级为5.5和3.0的地震波最大振幅,则=( )(参考数据:)
A.25 B.31.6 C.250 D.316
2.2022年诺贝尔物理学奖授予在量子领域做出贡献的法国、美国、奥地利科学家,我国于2021年成功研制出目前国际上超导量子比特数量最多的量子计算原型机“祖冲之号”,操控的超导量子比特为66个.已知1个超导量子比特共有“|0>,|1>”2种叠加态,2个超导量子比特共有“|00>,|01>,|10>,|11>”4种叠加态,3个超导量子比特共有“|000>,|001>,|010>,|011>,|100>,|101>,|110>,|111>”8种叠加态,…,只要增加1个超导量子比特,其叠加态的种数就呈指数级增长.设M个超导量子比特共有N种叠加态,且N是一个20位的数,则这样的M有( )个.(参考数据:lg2≈0.3010)
A.2 B.3 C.4 D.5
3.若二次函数y1=x2﹣ax+b的两个零点为2,3,则二次函数y2=bx2﹣ax﹣1的零点是( )
A.﹣1, B.1,﹣ C., D.﹣,﹣
4.某地投资a亿元进行基础建设,t年后产生的社会经济效益为f(t)=aeλt亿元,若该地投资基础建设4年后产生的社会经济效益是投资额的2倍,且再过t1年,该项投资产生的社会经济效益是投资额的16倍,则t1=( )
A.4 B.8 C.12 D.16
5.为了不断满足人民日益增长的美好生活需要,实现群众对舒适的居住条件、更优美的环境、更丰富的精神文化生活的追求,某大型广场正计划进行升级改造.改造的重点工程之一是新建一个长方形音乐喷泉综合体A1B1C1D1,该项目由长方形核心喷泉区ABCD(阴影部分)和四周绿化带组成.规划核心喷泉区的ABCD面积为1000m2,绿化带的宽分别为2m和5m(如图所示).当整个项目占地面积A1B1C1D1最小时,则核心喷泉区BC的长度为( )
A.20m B.50m C. D.100m
6.已知2a=15,log83=b,则2a﹣3b=( )
A.25 B.5 C. D.
7.已知2m=9n=6,则=( )
A.log618 B.log65 C.1 D.2
8.小明在调查某班小学生每月的人均零花钱时,得到了下列一组数据:
x/月份 2 3 4 5 6 …
y/元 1.40 2.56 5.31 11 21.30 …
请从模型,模型中选择一个合适的函数模型,并预测小学生零花钱首次超过300元的月份为( )(参考数据:lg3≈0.477,lg2≈0.301)
A.8 B.9 C.10 D.11
二.多选题(共4小题)
9.已知正数x,y,z满足等式2x=3y=6z,下列说法正确的是( )
A.x>y>z B.x>2y C. D.
10.已知2a=3b=6,则下列不等式中一定成立的是( )
A.a>b B.(a﹣1)2+(b﹣1)2>2
C.ab>5 D.a2+b2>8
11.已知2a=3b=6,则a,b满足( )
A.a>b B. C.ab>4 D.a+b>4
12.定义在R上的函数f(x)满足f(x+4)=f(x),函数f(x+1)为偶函数,且当x∈[1,3]时,f(x)=﹣x2+2x,则( )
A.f(x)的图象关于点(2,0)成中心对称
B.对任意整数k,f(2k)=0
C.f(x)的值域为[﹣3,1]
D.3f(x)﹣x+2=0的实数根个数为7
三.填空题(共4小题)
13.牛顿曾经提出了常温环境下的温度冷却模型:,其中t为时间(单位:min),θ0为环境温度,θ1为物体初始温度,θ为冷却后温度.假设在室内温度为20℃的情况下,一杯饮料由100℃降低到60℃需要20min,则此饮料从60℃降低到25℃需要 min.
14.已知函数f(x)=logax(a>0且a≠1)在区间上的最大值是2,则a= .
15.已知函数,若函数g(x)=f(x)﹣a有两个零点,则实数a的取值范围是 .
16.已知函数若方程f(x)=m有四个不同的实根x1,x2,x3,x4,满足x1<x2<x3<x4,则的取值范围是 .
四.解答题(共6小题)
17.化简求值:
(1);
(2).
18.已知x1,x2是方程x2﹣6x+k=0的两个实数根,且x12 x22﹣x1﹣x2=115.
(1)求k的取值.
(2)求x12+x22﹣8的值.
19.新学期开学季,成都某学校附近又新开了一家奶茶店,其中有一种名为“奶茶三兄弟”的饮品很受学生欢迎,老板费尽心思想在这种饮品上赚得第一桶金,其销售的价格在一学期不同周次有所变化.设开始时每杯定价10元,从第一次周开始每周涨价2元,5周后开始保持20元的价格平稳销售,10周后,学生的新鲜感已过,平均每周削价2元,直到16周周末,老板为了让学生安心准备期末考试复习而不挂念“三兄弟”,该饮品暂停销售.
(1)试求该饮品每杯价格p(元)与周次t,(t∈[1,16],t∈N)之间的函数关系式;
(2)若此饮品每杯成本价q(元)与周次t之间的关系是(t﹣8)2+12,t∈[1,16],t∈N,试问该饮品第几周每杯的销售利润最大,并求出最大值.
20.某种植户要倚靠院墙建一个高3m的长方体温室用于育苗,至多有54m2的材料可用于3面墙壁和顶棚的搭建,设温室中墙的边长分别为x,y,如图所示.
(1)写出:x,y满足的关系式;
(2)求温室体积的最大值.
21.已知函数y=ax2﹣(a+2)x+2,a∈R
(1)y<3﹣2x恒成立,求实数a的取值范围;
(2)若存在m>0使关于x的方程有四个不同的实根,求实数a的取值.
22.已知函数,函数,
(Ⅰ)已知直线l是曲线y=f(x)在点(0,f(0))处的切线,且l与曲线y=g(x)相切,求a的值;
(Ⅱ)若方程f(x)=g(x)有三个不同实数解,求实数a的取值范围.
参考答案
一.选择题(共8小题)
1--8DBBCB BCC
二.多选题(共4小题)
9.AC
10.ABD
11.ACD
12.BCD
三.填空题(共4小题)
13.60
14. 或4
15.[﹣1,0] {1}
16.(10,12)
四.解答题(共6小题)
17.解:(1)原式=
=;
(2)原式=
=4+2lg2+2lg2×lg5+2(lg5)2=4+2lg2+2lg5(lg2+lg5)
=4+2lg2+2lg5=4+2=6.
18.解:(1)由题意可得,x1+x2=6,x1x2=k,Δ=36﹣4k≥0,
所以k≤9,
∵x12 x22﹣x1﹣x2=k2﹣6=115,
所以k=11(舍)或k=﹣11,
(2)x12+x22﹣8==36+22﹣8=50.
19.解:(1)由题意得当0≤t≤5且t∈N*时,p=10+2t;
当5<t≤10且t∈N*时,p=20;
当10<t≤16且t∈N*时,p=40﹣2t,
综上所述,p=;
(2)由(1)得p=,(t﹣8)2+12,t∈[1,16],t∈N,
设利润为W,则W=p﹣q,
∴当0≤t≤5且t∈N*时,,W=10+2t﹣[﹣(t﹣8)2+12]=t2+6,
∴当t=5时,Wmax=9.125;
当5<t≤10且t∈N*时,W=20﹣[﹣(t﹣8)2+12]=t2﹣2t+16,
∴当t=8时,Wmax=8;
当10<t≤16且t∈N*时,W=40﹣2t﹣[﹣(t﹣8)2+12=t2﹣4t+36,
∴当t=11时,Wmax=7.125,
∵9.125>8>7.125,
∴该饮品第5周每杯的销售利润最大,且最大值9.125元.
20.解:(1)由题意得,顶棚所用材料的面积为xy,3面墙壁所用材料的面积为3x+6y,
∵至多有54m2的材料可用于3面墙壁和顶棚的搭建,
∴xy+3x+6y≤54(0<x<18,0<y<9).
(2)∵3x+6y≥2=6,
当且仅当x=2y时取等号,
∴xy+6≤xy+3x+6y≤54,
令=t>0,则t2+6t﹣54≤0,
解得0<t≤3,即0<xy≤18,
当且仅当x=6,y=3时取等号,
∴温室体积V=3xy≤54,
则温室体积的最大值为54m3.
21.解:(1)由题有ax2﹣(a+2)x+2<3﹣2x恒成立,
即ax2﹣ax﹣1<0恒成立,
当a=0时,﹣1<0恒成立,符合题意,
当a≠0时,则,得,
得﹣4<a<0,
综上,a的取值范围为(﹣4,0].
(2)当m>0时,令t=m++1≥2+1=3,
当且仅当m=1时取等号,
则关于x的方程f(|x|)=t可化为a|x|2﹣(a+2)|x|+2﹣t=0,
关于x的方程为a|x|2﹣(a+2)|x|+2﹣t=0有四个不等的实数根,
即ax2﹣(a+2)x+2﹣t=0,有两个不同的实数正根,
则,解得a<﹣2,
由(1)可知存在t∈[3,+∞)使得不等式4at+(a+2)2﹣8a>0成立,
故4a×3+(a+2)2﹣8a>0,即a2+8a+4>0,
解得a<﹣4﹣2或a>﹣4+2,
综上可得a<﹣4﹣2,
所以a的取值范围为(﹣∞,﹣4﹣2).
22.解:(Ⅰ)∵函数f(x)=x3﹣6x的导数为f′(x)=x2﹣6,
∴曲线y=f(x)在点(0,f(0))处的切线l的方程为y=﹣6x,
又曲线g(x)=上点(m,n)为切点的切线l的方程为,
∴,解得a=18.
(Ⅱ)记F(x)=f(x)﹣g(x)=x3﹣x2﹣6x﹣a,
F′(x)=x2﹣x﹣6,由F′(x)=0,可得x=﹣2或x=3.
当x<﹣2时,F′(x)>0,F(x)递增;
当﹣2<x<3时,F′(x)<0,F(x)递减;
当x>3时,F′(x)>0,F(x)递增.
可得x=﹣2时,F(x)取得极大值,且为﹣a,
x=3时,F(x)取得极小值,且为﹣a,
因为当x→+∞,F(x)→+∞;x→﹣∞,F(x)→﹣∞.
则方程f(x)=g(x)有三个不同实数解的等价条件为:
﹣a>0且﹣a<0,解得<a<.
故实数a的取值范围为
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
