专题11.1 计数原理与排列组合-2024年高考一轮复习数学人教A版专题 讲义 (含解析)
文档属性
| 名称 | 专题11.1 计数原理与排列组合-2024年高考一轮复习数学人教A版专题 讲义 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 277.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 14:14:43 | ||
图片预览




文档简介
专题11.1 计数原理与排列组合
1. 两个计数原理
名称 完成一件事的策略 完成这件事共有的方法
分类加法 计数原理 完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法 N=m+n种不同的方法
分步乘法 计数原理 完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法 N=m×n种不同的方法
2. 排列与组合
名称 定义
排列 从n个不同元素中取出m(m≤n)个元素 按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列
组合 作为一组,叫做从n个不同元素中取出m个元素的一个组合
3.排列数与组合数
(1)排列数:从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数叫做从n个不同元素中取出m个元素的排列数,用A表示.
(2)组合数:从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用C表示.
【重要结论】
排列数、组合数的公式及性质
公式 A=n(n-1)(n-2)…(n-m+1)=
C===
性质 0!=1,A=n!
C=C,C=C+C
1.【人教A版选择性必修三 习题6.1 第3题 P11】如图,电路中共有个电阻与个灯泡,若灯泡不亮,则因电阻断路的情况共有 种
2.【人教A版选择性必修三 习题6.2 第5题 P26】高一军训结束后,共有人被评为国旗队旗手,其中一班甲、乙人、二班人、三班人.
(1)在某次训练中,辅导员从中选择人均来自不同班级站一排检验步法,有多少种不同的排法;
某电影院邀请该名旗手免费观看某场电影,由于学习时间紧,去几个人学生自己决定,但其中甲、乙两人要么都去,要么都不去,一共有多少种去法?
【方法储备】
利用分类加法计数原理计数时的解题流程
利用分步乘法计数原理解决问题的策略
(1)利用分步乘法计数原理解决问题时要注意按事件发生的过程来合理分步,即分步是有先后顺序的,并且分步必须满足:完成一件事的各个步骤是相互依存的,只有各个步骤都完成了,才算完成这件事.
(2)分步必须满足的两个条件:一是各步骤相互独立,互不干扰;二是步与步之间确保连续,逐步完成.
【典例精讲】
例1. (2023·山东省菏泽市·期中考试) 为提升学生的数学素养,某中学特开设了“数学史”“数学建模”“古今数学思想”“数学探究”“中国大学先修课程微积分学习指导”五门选修课程,要求每位同学每学年至多选四门,高一到高二两学年必须将五门选修课程选完,则每位同学不同的选修方式为( )
A. B. C. D.
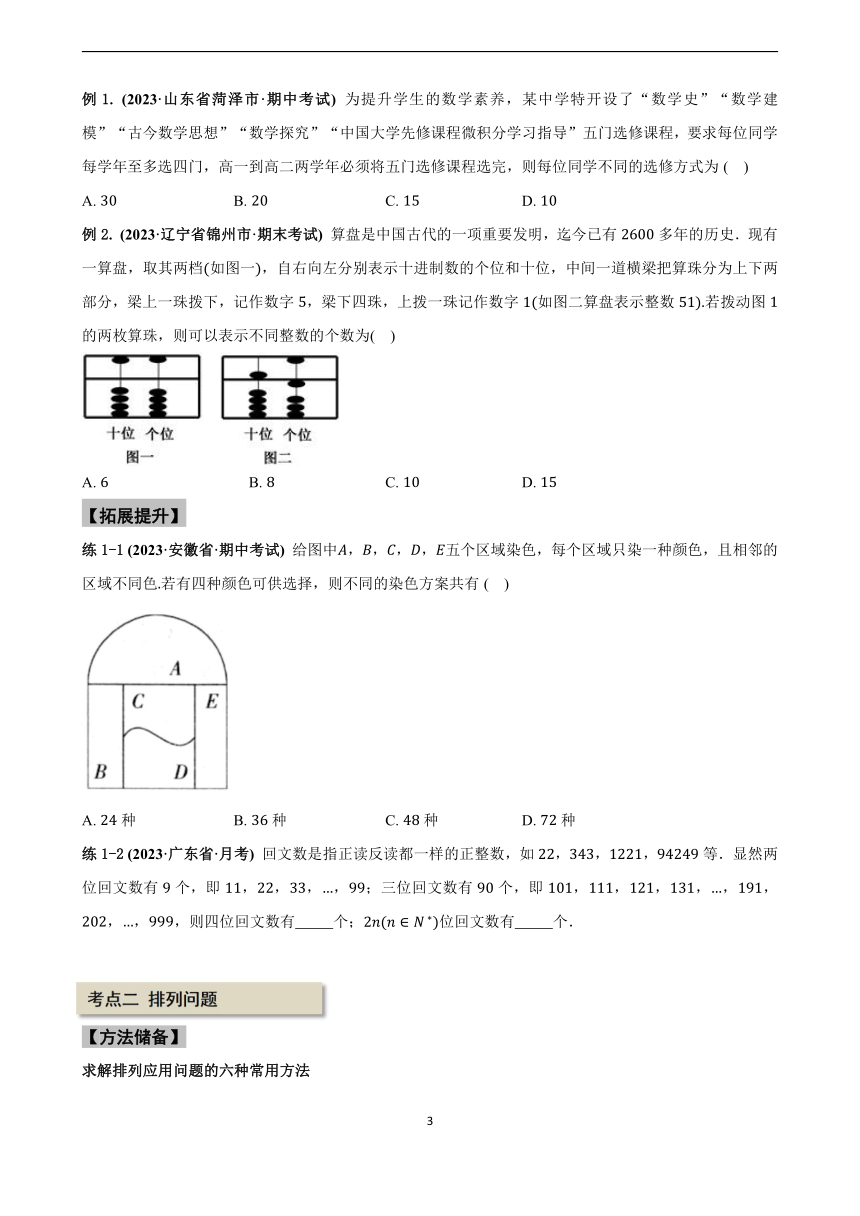
例2. (2023·辽宁省锦州市·期末考试) 算盘是中国古代的一项重要发明,迄今已有多年的历史.现有一算盘,取其两档如图一,自右向左分别表示十进制数的个位和十位,中间一道横梁把算珠分为上下两部分,梁上一珠拨下,记作数字,梁下四珠,上拨一珠记作数字如图二算盘表示整数若拨动图的两枚算珠,则可以表示不同整数的个数为( )
A. B. C. D.
【拓展提升】
练1-1 (2023·安徽省·期中考试) 给图中,,,,五个区域染色,每个区域只染一种颜色,且相邻的区域不同色若有四种颜色可供选择,则不同的染色方案共有( )
A. 种 B. 种 C. 种 D. 种
练1-2 (2023·广东省·月考) 回文数是指正读反读都一样的正整数,如,,,等.显然两位回文数有个,即,,,,;三位回文数有个,即,,,,,,,,,则四位回文数有 个;位回文数有 个.
【方法储备】
求解排列应用问题的六种常用方法
【典例精讲】
例3. (2023·浙江省·单元测试)位教师和位学生排成一排合影留念,师生相间的排法种数为( )
A. B. C. D.
例4. (2023·黑龙江省·期末考试) 甲、乙、丙、丁、戊名同学进行校园厨艺总决赛,决出第名到第名的名次甲和乙去询问成绩,回答者对甲说:“很遗憾,你没有得到冠军”对乙说:“你和甲的名次相邻”从这两个回答分析,人的名次排列情况种数为( )
A. B. C. D.
例5. (2023·全国·单元测试) 在一次学校组织的研究性学习成果报告会上,有共项成果要汇报,如果成果不能最先汇报,而按先后顺序汇报不一定相邻,那么不同的汇报安排种数为( )
A. B. C. D.
【拓展提升】
练2-1 (2023·辽宁省·联考题) 甲、乙、丙位志愿者安排在周一至周五的天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面,不同的安排方法共有( )
A. 种 B. 种 C. 种 D. 种
练2-2 (2023·广东省中山市·联考题) 将诗集诗经、唐诗三百首,戏剧牡丹亭,四大名著红楼梦、西游记、三国演义、水浒传本书放在一排,下面结论成立的是( )
A. 戏剧放在中间的不同放法有种
B. 诗集相邻的不同放法有种
C. 四大名著互不相邻的不同放法有种
D. 四大名著不放在两端的不同放法有种
练2-3 (2023·全国·模拟) 有对夫妇和,共人参加一场婚宴,他们被安排在一张有个座位的圆桌上就餐旋转之后算相同坐法.
若对夫妇都相邻而坐,,相邻而坐,共有多少种坐法?
对夫妇都相邻而坐,其中甲、乙二人的太太是闺蜜要相邻而坐,,不相邻,共有多少种坐法?
【方法储备】
组合问题的两类题型及求解方法
(1)“含有”或“不含有”某些元素的组合题型:“含”,则先将这些元素取出,再由另外的元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.
(2)“至少”或“至多”含有几个元素的组合题型:解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解.用直接法和间接法都可以求解,通常用直接法,分类复杂时,考虑逆向思维,用间接法处理.
【典例精讲】
例6. (2023·江苏省盐城市·期中考试) 为了庆祝新年的到来,某校“皮影戏”社团的名男同学,名女同学计划组成人代表队代表本校参加市级“皮影戏”比赛,该代表队中有队长,副队长各一名,剩余两名为队员若现要求代表队中至少有一名女同学,一共有 种可能.
例7. (2023·广东省中山市·单元测试)某班有名学生,其中正、副班长各人,现选派人参加一项活动,要求正、副班长至少有人参加,问共有多少种选派方法?下面是学生提供的四种计算方法正确的算法为( )
A. ; B. ;
C. ; D. .
【拓展提升】
练3-1 (2023·山东省·阶段测试)名运动员中有名老队员和名新队员,现从中选人参加团体比赛,要求老队员至多人入选且新队员甲不能入选的选法有( )
A. 种 B. 种 C. 种 D. 种
练3-2 (2023·云南省·模拟) 在新高考方案中,选择性考试科目有:物理、化学、生物、政治、历史、地理门学生根据高校的要求,结合自身特长兴趣,首先在物理、历史门科目中选择门,再从政治、地理、化学、生物门科目中选择门,考试成绩计入考生总分,作为统一高考招生录取的依据某学生想在物理、化学、生物、政治、历史、地理这门课程中选三门作为选考科目,下列说法正确的是( )
A. 若任意选科,选法总数为
B. 若化学必选,选法总数为
C. 若政治和地理至少选一门,选法总数为
D. 若物理必选,化学、生物至少选一门,选法总数为
【方法储备】
分组、分配问题是排列与组合的综合问题,解题思想是先分组后分配
(1)分组问题属于“组合”问题,常见的分组方法有三种:
①完全均匀分组,每组元素的个数都相等;
②部分均匀分组,应注意不要重复;
③完全非均匀分组,这种分组不考虑重复现象.
(2)分配问题属于“排列”问题,常见的分配方法有三种:
①相同元素的分配问题,常用“挡板法”;
②不同元素的分配问题,利用分步乘法计数原理,先分组,后分配;
③有限制条件的分配问题,采用分类求解.
提醒:对于部分均分问题,若有m组元素个数相等,则分组时应除以m!
【典例精讲】
例8. (2023·北京市海淀区期末测试) 从这本不同的文学读物中选出本分给甲、乙、丙名学生每人一本如果甲不得读物,则不同的分法种数为( )
A. B. C. D.
例9. (2023·湖北省联考) 将名志愿者含甲、乙、丙安排到三个地区做环保宣传工作,每个地区至少需要安排人,则甲、乙、丙人恰好被安排到同一个地区的安排方法总数为( )
A. B. C. D.
【拓展提升】
练4-1 (2022·河北省保定市·月考试卷) 把座位编号为,,,,,的张电影票分给甲、乙、丙、丁四个人,每人至少分一张,至多分两张,且分得的两张票必须是连号的,那么不同分法种数为( )
A. B. C. D.
练4-2 (2023·山东省烟台市·单元测试) 如图,一个正方形花圃被分成份.
若给这个部分种植花,要求相邻两部分种植不同颜色的花,己知现有红、黄、蓝、绿种颜色不同的花,求有多少种不同的种植方法?
若向这个部分放入个不同的盆栽,要求每个部分都有盆栽,问有多少种不同的放法?
1. (2023·安徽省阜阳市·月考试卷)位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知位同学之间共进行了次交换,则收到份纪念品的同学人数为( )
A. 或 B. 或 C. 或 D. 或
2. (2023·广东省广州市·期末考试) 学校乒乓团体比赛采用场胜制场单打,每支球队派名运动员参赛,前场比赛每名运动员各出场次,其中第、位出场的运动员在后场比赛中还将各出场次,假设某球队派甲、乙、丙名运动员参加比赛,则所有可能的出场情况的种数为( )
A. B. C. D.
3. (2023·安徽省·期中考试) 在某城市中,,两地之间有如图所示的道路网,甲随机沿路网选择一条最短路径,从地出发去往地下列结论正确的有( )
A. 不同的路径共有条
B. 不同的路径共有条
C. 若甲途经地,则不同的路径共有条
D. 若甲途经地,且不经过地,则不同的路径共有条
【答案解析】
1.【人教A版选择性必修三 习题6.1 第3题 P11】
解:每个电阻都有断路与通路两种状态,灯泡不亮可以分种情况讨论:
①个电阻断路,此时只有种情况;
②个电阻断路,此时有种情况
③个电阻断路,此时只有种情况.
根据分类加法计数原理,可知灯泡因电阻断路不亮的情况共有种.
故答案为.
2.【人教A版选择性必修三 习题6.2 第5题 P26】
解:从每个班里各选一人排列共有 种方法;
方法一:把一班的甲乙两人当作个人,这样相当于共有个人,
这人最少可能去个,最多可能去个甲乙视为人,
故共有种 ;
方法二:把一班的甲乙两人当作个人,
这样相当于共有个人每个人去与不去均有两种情况,
根据乘法原理种
例1.解:由题意,每门选修课程被安排到高一到高二两学年都有种安排方法,
故共有种安排方法,
其中五门选修课程安排到同一学年的情况有种,
则每位同学不同的选修方式为种.
故选A.
例2.解:拨动两枚算珠可分为以下三类:
在个位上拨动两枚,可表示个不同整数.
同理在十位上拨动两枚,可表示个不同整数.
在个位、十位上分别拨动一枚,由分步乘法计数原理易得,可表示个不同整数.
所以,根据分类加法计数原理,一共可表示个不同整数.
故选:.
练1-1.解:按的秩序依次染色,
当,同色时,共有种不同的染色方案,
当,不同色时,共有种不同的染色方案,
所以共有种不同的染色方案.
故选D.
练1-2.解:由题意,可知四位回文数的特点为中间两位数是相同的,千位数和个位数相同但都不能为,
第一步,选千位数和个位数,共有种选法;第二步,选中间两位数,共有种选法.
由分步乘法计数原理可得,四位回文数共有个.
在位回文数中,第一步,先选左边的第个数,共有种选法;
第二步,选左边的第个数,共有种选法第步,选左边的第个数,共有种选法.
由分步乘法计数原理可得,位回文数共有个.
故答案为:.
例3.解:根据题意,位教师全排列,有种排法,
排好后,有个空位,选择其中连续的个空位,安排位学生,有种排法,
则共有种排法.
故选C.
例4. 解:由题意知乙和甲的名次相邻.排列数为
甲得到冠军且甲乙名次相邻的排列数为
所以甲没得到冠军且甲乙名次相邻的排列数为
故答案为C.
例5. 解:不考虑限制条件共有种,最先汇报共有种,
如果不能最先汇报,而按先后顺序汇报不一定相邻有.
故选:.
练2-1.解:根据题意,要求甲安排在另外两位前面,则甲有种分配方法,即甲在星期一、二、三;
分种情况讨论可得,甲在星期一有种安排方法,
甲在星期二有种安排方法,
甲在星期三有种安排方法,
总共有种;
故选A.
练2-2.解: 戏剧只有一本放在中间,所以其余本书可以全排列,共有种不同排列方法,故选项A错误;
B. 诗集共本,把诗集当成一本与其它本书全排列,不同放法有种,这两本又可交换位置,所以不同放法数为, 故选项B错误;
C.四大名著若互不相邻,只能在这四本书的个空隙中放置其他书,共有种放法,这四本书又可以全排列,
所以不同放法数为,故选项C错误;
D. 先在诗集和戏剧书中选本放到两端,有 种不同放法,再把剩下的本书放到剩下的个位置,有种不同放法,因此共有种不同放法,故选项D正确
故选:D.
练2-3.解:若对夫妇都相邻,,相邻,可将每对夫妇划分为组,,划分为组,再将这组人围坐成一圈,共有种坐法,
由于每一组内两人还有顺序问题,所以共有种坐法;
分成三步来完成,
第一步,排甲、乙二人的太太的座位,有种坐法,甲、乙二人的座位也随之确定,
第二步,排其余对夫妇的座位,有种坐法,
第三步,排,二人的座位,有种坐法,
根据分步乘法计数原理,共有种坐法.
例6.解:若代表队中有名女同学,此时共有种可能,
若女同学的人数为,
则共有 种可能,所以一共有种可能.
故答案为.
例7. 解:①正、副班长中有一个参加,有种选法;
正、副班长中有两个参加,有种选法;
则正、副班长至少有人参加共有种选法,可知A正确;
②从人中选人,有种选法,选取的人中没有班长,则有中选法,
则正、副班长至少有人参加的有种选法,可知B正确;
③从两个班长中选一个,再从余下的人中选个,有种选法,
其中选了两个班长的情况重复计算了一次,选了两个班长有种选法,
则正、副班长至少有人参加的有种选法,可知C错误,D正确.
故选ABD.
练3-1 .解:分两类进行讨论:
人中有名老队员、名新队员,共有种选法;
人全部是新队员,共有种选法;
老队员至多人入选且新队员甲不能入选的选法有种,
故选A.
练3-2 .解:对于项,首先在物理、历史门科目中选择门,再从政治、地理、化学、生物门科目中选择门,则选法总数为,故A项错误;对于项,首先在物理、历史门科目中选择门,再从政治、地理、生物门科目中选择门,则选法总数为,故B项正确;对于项,分政治和地理都选和政治和地理仅选一门,则选法总数为,故C项错误;对于项,物理必选,分化学、生物都选和化学、生物仅选一门,则选法总数为,故D项正确.
故选:.
例8.解:若 读物没被选出,则选出的 读物直接全排列分给 人,有 种方法;
若 读物被选出,然后选其他的读物,有 种,甲有 种读物可选,其余两本书全排列分给乙丙有 种方法,共 种.
故一共有 种.
故选:
例9. 解:先分类讨论人员分组情况.
当甲、乙、丙所在组恰有人时,余下人分成组,有种方法
当甲、乙、丙所在组恰有人时,先从其他人中选人到这组,再将余下人分成组,
有种方法
当甲、乙、丙所在组恰有人时,先从其他人中选人到这组,余下人分成组,有种方法
当甲、乙、丙所在组恰有人时,先从其他人中选人到这组,余下人分成组,有种方法.
再将三组人员分配到三个地区.
因为这三组分配到三个地区有种方法,所以安排方法总数为.
故选C.
练4-1 .解:根据题意,分步进行分析:
①先将票分为符合条件的份;
由题意,人分张票,且每人至少一张,至多两张,则两人一张,人张,且分得的票必须是连号的,相当于将、、、、、这六个数用个板子隔开,分为四部分且不存在三连号,易得在个空位插个板子,共有种情况,但其中有种是人张票的,故有种情况符合题意,
②将分好的份对应到个人,进行全排列即可,有种情况;
故有种情况.
故选B.
练4-2.解:先对部分种植,有种不同的种植方法;再对部分种植,有种不同的种植方法;
对部分种植进行分类:
①若与相同,有种不同的种植方法,有种不同的种植方法,共有种;
②若与不同,有种不同的种植方法,有种不同的种植方法,有种不同的种植方法,
共有种;
综上所述,共有种种植方法;
将个盆栽分成组,有种分法:
①若分成的组,有种分法;
②若分成的组,有种分法;
将分好的组全排列,对应个部分,则一共有种分法.
1. 解:任意两位同学之间交换纪念品共要交换次,
如果都完全交换,每个人都要交换次,也就是每人得到份纪念品.
现在位同学总共交换了次,少交换了次,
这次若不涉及同一人,则收到份纪念品的同学有人,
若涉及同一个人,则收到份纪念品的同学有人.
故选D.
2. 解:分以下几种情况讨论:
①若 场比赛结束,此时,不同的出场情况种数为 种;
②若 场比赛结束,则第 场为第 或第 位运动员出场,
此时,不同的出场情况种数为 种;
③若 场比赛结束,则第, 场为第 和第 位运动员各出场 次,
此时,不同的出场情况种数为 种.
综上所述,不同的出场情况种数为 种.
故选:.
3. 解:由图可知,从地出发去往地的最短路径共包含步,其中步向上,步向右,且前步中,至少有步向上,则不同的路径共有条.
若甲途经地,则不同的路径共有条.
若甲途经地,且不经过地,则不同的路径共有条.
故选ACD.
2
1. 两个计数原理
名称 完成一件事的策略 完成这件事共有的方法
分类加法 计数原理 完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法 N=m+n种不同的方法
分步乘法 计数原理 完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法 N=m×n种不同的方法
2. 排列与组合
名称 定义
排列 从n个不同元素中取出m(m≤n)个元素 按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列
组合 作为一组,叫做从n个不同元素中取出m个元素的一个组合
3.排列数与组合数
(1)排列数:从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数叫做从n个不同元素中取出m个元素的排列数,用A表示.
(2)组合数:从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用C表示.
【重要结论】
排列数、组合数的公式及性质
公式 A=n(n-1)(n-2)…(n-m+1)=
C===
性质 0!=1,A=n!
C=C,C=C+C
1.【人教A版选择性必修三 习题6.1 第3题 P11】如图,电路中共有个电阻与个灯泡,若灯泡不亮,则因电阻断路的情况共有 种
2.【人教A版选择性必修三 习题6.2 第5题 P26】高一军训结束后,共有人被评为国旗队旗手,其中一班甲、乙人、二班人、三班人.
(1)在某次训练中,辅导员从中选择人均来自不同班级站一排检验步法,有多少种不同的排法;
某电影院邀请该名旗手免费观看某场电影,由于学习时间紧,去几个人学生自己决定,但其中甲、乙两人要么都去,要么都不去,一共有多少种去法?
【方法储备】
利用分类加法计数原理计数时的解题流程
利用分步乘法计数原理解决问题的策略
(1)利用分步乘法计数原理解决问题时要注意按事件发生的过程来合理分步,即分步是有先后顺序的,并且分步必须满足:完成一件事的各个步骤是相互依存的,只有各个步骤都完成了,才算完成这件事.
(2)分步必须满足的两个条件:一是各步骤相互独立,互不干扰;二是步与步之间确保连续,逐步完成.
【典例精讲】
例1. (2023·山东省菏泽市·期中考试) 为提升学生的数学素养,某中学特开设了“数学史”“数学建模”“古今数学思想”“数学探究”“中国大学先修课程微积分学习指导”五门选修课程,要求每位同学每学年至多选四门,高一到高二两学年必须将五门选修课程选完,则每位同学不同的选修方式为( )
A. B. C. D.
例2. (2023·辽宁省锦州市·期末考试) 算盘是中国古代的一项重要发明,迄今已有多年的历史.现有一算盘,取其两档如图一,自右向左分别表示十进制数的个位和十位,中间一道横梁把算珠分为上下两部分,梁上一珠拨下,记作数字,梁下四珠,上拨一珠记作数字如图二算盘表示整数若拨动图的两枚算珠,则可以表示不同整数的个数为( )
A. B. C. D.
【拓展提升】
练1-1 (2023·安徽省·期中考试) 给图中,,,,五个区域染色,每个区域只染一种颜色,且相邻的区域不同色若有四种颜色可供选择,则不同的染色方案共有( )
A. 种 B. 种 C. 种 D. 种
练1-2 (2023·广东省·月考) 回文数是指正读反读都一样的正整数,如,,,等.显然两位回文数有个,即,,,,;三位回文数有个,即,,,,,,,,,则四位回文数有 个;位回文数有 个.
【方法储备】
求解排列应用问题的六种常用方法
【典例精讲】
例3. (2023·浙江省·单元测试)位教师和位学生排成一排合影留念,师生相间的排法种数为( )
A. B. C. D.
例4. (2023·黑龙江省·期末考试) 甲、乙、丙、丁、戊名同学进行校园厨艺总决赛,决出第名到第名的名次甲和乙去询问成绩,回答者对甲说:“很遗憾,你没有得到冠军”对乙说:“你和甲的名次相邻”从这两个回答分析,人的名次排列情况种数为( )
A. B. C. D.
例5. (2023·全国·单元测试) 在一次学校组织的研究性学习成果报告会上,有共项成果要汇报,如果成果不能最先汇报,而按先后顺序汇报不一定相邻,那么不同的汇报安排种数为( )
A. B. C. D.
【拓展提升】
练2-1 (2023·辽宁省·联考题) 甲、乙、丙位志愿者安排在周一至周五的天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面,不同的安排方法共有( )
A. 种 B. 种 C. 种 D. 种
练2-2 (2023·广东省中山市·联考题) 将诗集诗经、唐诗三百首,戏剧牡丹亭,四大名著红楼梦、西游记、三国演义、水浒传本书放在一排,下面结论成立的是( )
A. 戏剧放在中间的不同放法有种
B. 诗集相邻的不同放法有种
C. 四大名著互不相邻的不同放法有种
D. 四大名著不放在两端的不同放法有种
练2-3 (2023·全国·模拟) 有对夫妇和,共人参加一场婚宴,他们被安排在一张有个座位的圆桌上就餐旋转之后算相同坐法.
若对夫妇都相邻而坐,,相邻而坐,共有多少种坐法?
对夫妇都相邻而坐,其中甲、乙二人的太太是闺蜜要相邻而坐,,不相邻,共有多少种坐法?
【方法储备】
组合问题的两类题型及求解方法
(1)“含有”或“不含有”某些元素的组合题型:“含”,则先将这些元素取出,再由另外的元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.
(2)“至少”或“至多”含有几个元素的组合题型:解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解.用直接法和间接法都可以求解,通常用直接法,分类复杂时,考虑逆向思维,用间接法处理.
【典例精讲】
例6. (2023·江苏省盐城市·期中考试) 为了庆祝新年的到来,某校“皮影戏”社团的名男同学,名女同学计划组成人代表队代表本校参加市级“皮影戏”比赛,该代表队中有队长,副队长各一名,剩余两名为队员若现要求代表队中至少有一名女同学,一共有 种可能.
例7. (2023·广东省中山市·单元测试)某班有名学生,其中正、副班长各人,现选派人参加一项活动,要求正、副班长至少有人参加,问共有多少种选派方法?下面是学生提供的四种计算方法正确的算法为( )
A. ; B. ;
C. ; D. .
【拓展提升】
练3-1 (2023·山东省·阶段测试)名运动员中有名老队员和名新队员,现从中选人参加团体比赛,要求老队员至多人入选且新队员甲不能入选的选法有( )
A. 种 B. 种 C. 种 D. 种
练3-2 (2023·云南省·模拟) 在新高考方案中,选择性考试科目有:物理、化学、生物、政治、历史、地理门学生根据高校的要求,结合自身特长兴趣,首先在物理、历史门科目中选择门,再从政治、地理、化学、生物门科目中选择门,考试成绩计入考生总分,作为统一高考招生录取的依据某学生想在物理、化学、生物、政治、历史、地理这门课程中选三门作为选考科目,下列说法正确的是( )
A. 若任意选科,选法总数为
B. 若化学必选,选法总数为
C. 若政治和地理至少选一门,选法总数为
D. 若物理必选,化学、生物至少选一门,选法总数为
【方法储备】
分组、分配问题是排列与组合的综合问题,解题思想是先分组后分配
(1)分组问题属于“组合”问题,常见的分组方法有三种:
①完全均匀分组,每组元素的个数都相等;
②部分均匀分组,应注意不要重复;
③完全非均匀分组,这种分组不考虑重复现象.
(2)分配问题属于“排列”问题,常见的分配方法有三种:
①相同元素的分配问题,常用“挡板法”;
②不同元素的分配问题,利用分步乘法计数原理,先分组,后分配;
③有限制条件的分配问题,采用分类求解.
提醒:对于部分均分问题,若有m组元素个数相等,则分组时应除以m!
【典例精讲】
例8. (2023·北京市海淀区期末测试) 从这本不同的文学读物中选出本分给甲、乙、丙名学生每人一本如果甲不得读物,则不同的分法种数为( )
A. B. C. D.
例9. (2023·湖北省联考) 将名志愿者含甲、乙、丙安排到三个地区做环保宣传工作,每个地区至少需要安排人,则甲、乙、丙人恰好被安排到同一个地区的安排方法总数为( )
A. B. C. D.
【拓展提升】
练4-1 (2022·河北省保定市·月考试卷) 把座位编号为,,,,,的张电影票分给甲、乙、丙、丁四个人,每人至少分一张,至多分两张,且分得的两张票必须是连号的,那么不同分法种数为( )
A. B. C. D.
练4-2 (2023·山东省烟台市·单元测试) 如图,一个正方形花圃被分成份.
若给这个部分种植花,要求相邻两部分种植不同颜色的花,己知现有红、黄、蓝、绿种颜色不同的花,求有多少种不同的种植方法?
若向这个部分放入个不同的盆栽,要求每个部分都有盆栽,问有多少种不同的放法?
1. (2023·安徽省阜阳市·月考试卷)位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知位同学之间共进行了次交换,则收到份纪念品的同学人数为( )
A. 或 B. 或 C. 或 D. 或
2. (2023·广东省广州市·期末考试) 学校乒乓团体比赛采用场胜制场单打,每支球队派名运动员参赛,前场比赛每名运动员各出场次,其中第、位出场的运动员在后场比赛中还将各出场次,假设某球队派甲、乙、丙名运动员参加比赛,则所有可能的出场情况的种数为( )
A. B. C. D.
3. (2023·安徽省·期中考试) 在某城市中,,两地之间有如图所示的道路网,甲随机沿路网选择一条最短路径,从地出发去往地下列结论正确的有( )
A. 不同的路径共有条
B. 不同的路径共有条
C. 若甲途经地,则不同的路径共有条
D. 若甲途经地,且不经过地,则不同的路径共有条
【答案解析】
1.【人教A版选择性必修三 习题6.1 第3题 P11】
解:每个电阻都有断路与通路两种状态,灯泡不亮可以分种情况讨论:
①个电阻断路,此时只有种情况;
②个电阻断路,此时有种情况
③个电阻断路,此时只有种情况.
根据分类加法计数原理,可知灯泡因电阻断路不亮的情况共有种.
故答案为.
2.【人教A版选择性必修三 习题6.2 第5题 P26】
解:从每个班里各选一人排列共有 种方法;
方法一:把一班的甲乙两人当作个人,这样相当于共有个人,
这人最少可能去个,最多可能去个甲乙视为人,
故共有种 ;
方法二:把一班的甲乙两人当作个人,
这样相当于共有个人每个人去与不去均有两种情况,
根据乘法原理种
例1.解:由题意,每门选修课程被安排到高一到高二两学年都有种安排方法,
故共有种安排方法,
其中五门选修课程安排到同一学年的情况有种,
则每位同学不同的选修方式为种.
故选A.
例2.解:拨动两枚算珠可分为以下三类:
在个位上拨动两枚,可表示个不同整数.
同理在十位上拨动两枚,可表示个不同整数.
在个位、十位上分别拨动一枚,由分步乘法计数原理易得,可表示个不同整数.
所以,根据分类加法计数原理,一共可表示个不同整数.
故选:.
练1-1.解:按的秩序依次染色,
当,同色时,共有种不同的染色方案,
当,不同色时,共有种不同的染色方案,
所以共有种不同的染色方案.
故选D.
练1-2.解:由题意,可知四位回文数的特点为中间两位数是相同的,千位数和个位数相同但都不能为,
第一步,选千位数和个位数,共有种选法;第二步,选中间两位数,共有种选法.
由分步乘法计数原理可得,四位回文数共有个.
在位回文数中,第一步,先选左边的第个数,共有种选法;
第二步,选左边的第个数,共有种选法第步,选左边的第个数,共有种选法.
由分步乘法计数原理可得,位回文数共有个.
故答案为:.
例3.解:根据题意,位教师全排列,有种排法,
排好后,有个空位,选择其中连续的个空位,安排位学生,有种排法,
则共有种排法.
故选C.
例4. 解:由题意知乙和甲的名次相邻.排列数为
甲得到冠军且甲乙名次相邻的排列数为
所以甲没得到冠军且甲乙名次相邻的排列数为
故答案为C.
例5. 解:不考虑限制条件共有种,最先汇报共有种,
如果不能最先汇报,而按先后顺序汇报不一定相邻有.
故选:.
练2-1.解:根据题意,要求甲安排在另外两位前面,则甲有种分配方法,即甲在星期一、二、三;
分种情况讨论可得,甲在星期一有种安排方法,
甲在星期二有种安排方法,
甲在星期三有种安排方法,
总共有种;
故选A.
练2-2.解: 戏剧只有一本放在中间,所以其余本书可以全排列,共有种不同排列方法,故选项A错误;
B. 诗集共本,把诗集当成一本与其它本书全排列,不同放法有种,这两本又可交换位置,所以不同放法数为, 故选项B错误;
C.四大名著若互不相邻,只能在这四本书的个空隙中放置其他书,共有种放法,这四本书又可以全排列,
所以不同放法数为,故选项C错误;
D. 先在诗集和戏剧书中选本放到两端,有 种不同放法,再把剩下的本书放到剩下的个位置,有种不同放法,因此共有种不同放法,故选项D正确
故选:D.
练2-3.解:若对夫妇都相邻,,相邻,可将每对夫妇划分为组,,划分为组,再将这组人围坐成一圈,共有种坐法,
由于每一组内两人还有顺序问题,所以共有种坐法;
分成三步来完成,
第一步,排甲、乙二人的太太的座位,有种坐法,甲、乙二人的座位也随之确定,
第二步,排其余对夫妇的座位,有种坐法,
第三步,排,二人的座位,有种坐法,
根据分步乘法计数原理,共有种坐法.
例6.解:若代表队中有名女同学,此时共有种可能,
若女同学的人数为,
则共有 种可能,所以一共有种可能.
故答案为.
例7. 解:①正、副班长中有一个参加,有种选法;
正、副班长中有两个参加,有种选法;
则正、副班长至少有人参加共有种选法,可知A正确;
②从人中选人,有种选法,选取的人中没有班长,则有中选法,
则正、副班长至少有人参加的有种选法,可知B正确;
③从两个班长中选一个,再从余下的人中选个,有种选法,
其中选了两个班长的情况重复计算了一次,选了两个班长有种选法,
则正、副班长至少有人参加的有种选法,可知C错误,D正确.
故选ABD.
练3-1 .解:分两类进行讨论:
人中有名老队员、名新队员,共有种选法;
人全部是新队员,共有种选法;
老队员至多人入选且新队员甲不能入选的选法有种,
故选A.
练3-2 .解:对于项,首先在物理、历史门科目中选择门,再从政治、地理、化学、生物门科目中选择门,则选法总数为,故A项错误;对于项,首先在物理、历史门科目中选择门,再从政治、地理、生物门科目中选择门,则选法总数为,故B项正确;对于项,分政治和地理都选和政治和地理仅选一门,则选法总数为,故C项错误;对于项,物理必选,分化学、生物都选和化学、生物仅选一门,则选法总数为,故D项正确.
故选:.
例8.解:若 读物没被选出,则选出的 读物直接全排列分给 人,有 种方法;
若 读物被选出,然后选其他的读物,有 种,甲有 种读物可选,其余两本书全排列分给乙丙有 种方法,共 种.
故一共有 种.
故选:
例9. 解:先分类讨论人员分组情况.
当甲、乙、丙所在组恰有人时,余下人分成组,有种方法
当甲、乙、丙所在组恰有人时,先从其他人中选人到这组,再将余下人分成组,
有种方法
当甲、乙、丙所在组恰有人时,先从其他人中选人到这组,余下人分成组,有种方法
当甲、乙、丙所在组恰有人时,先从其他人中选人到这组,余下人分成组,有种方法.
再将三组人员分配到三个地区.
因为这三组分配到三个地区有种方法,所以安排方法总数为.
故选C.
练4-1 .解:根据题意,分步进行分析:
①先将票分为符合条件的份;
由题意,人分张票,且每人至少一张,至多两张,则两人一张,人张,且分得的票必须是连号的,相当于将、、、、、这六个数用个板子隔开,分为四部分且不存在三连号,易得在个空位插个板子,共有种情况,但其中有种是人张票的,故有种情况符合题意,
②将分好的份对应到个人,进行全排列即可,有种情况;
故有种情况.
故选B.
练4-2.解:先对部分种植,有种不同的种植方法;再对部分种植,有种不同的种植方法;
对部分种植进行分类:
①若与相同,有种不同的种植方法,有种不同的种植方法,共有种;
②若与不同,有种不同的种植方法,有种不同的种植方法,有种不同的种植方法,
共有种;
综上所述,共有种种植方法;
将个盆栽分成组,有种分法:
①若分成的组,有种分法;
②若分成的组,有种分法;
将分好的组全排列,对应个部分,则一共有种分法.
1. 解:任意两位同学之间交换纪念品共要交换次,
如果都完全交换,每个人都要交换次,也就是每人得到份纪念品.
现在位同学总共交换了次,少交换了次,
这次若不涉及同一人,则收到份纪念品的同学有人,
若涉及同一个人,则收到份纪念品的同学有人.
故选D.
2. 解:分以下几种情况讨论:
①若 场比赛结束,此时,不同的出场情况种数为 种;
②若 场比赛结束,则第 场为第 或第 位运动员出场,
此时,不同的出场情况种数为 种;
③若 场比赛结束,则第, 场为第 和第 位运动员各出场 次,
此时,不同的出场情况种数为 种.
综上所述,不同的出场情况种数为 种.
故选:.
3. 解:由图可知,从地出发去往地的最短路径共包含步,其中步向上,步向右,且前步中,至少有步向上,则不同的路径共有条.
若甲途经地,则不同的路径共有条.
若甲途经地,且不经过地,则不同的路径共有条.
故选ACD.
2
同课章节目录
