专题12.3 离散型随机变量及其分布列、数字特征 -2024年高考一轮复习数学人教A版专题讲义(教案)(含答案)
文档属性
| 名称 | 专题12.3 离散型随机变量及其分布列、数字特征 -2024年高考一轮复习数学人教A版专题讲义(教案)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 161.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 14:10:36 | ||
图片预览




文档简介
专题12.3 离散型随机变量及其分布列、数字特征
1.离散型随机变量
一般地,对于随机试验样本空间中的每个样本点都有唯一的实数与之对应,我们称为随机变量.
表示:用大写英文字母表示随机变量,如;用小写英文字母表示随机变量的取值,如.
2.离散型随机变量的分布列
一般地,设离散型随机变量的可能取值为,我们称取每一个值的概率
为的概率分布列,简称分布列.
与函数的表示方法类似,离散型随机变量的分布列也可以用表格表示:
… …
… …
3.离散型随机变量的分布列的性质
⑴;
⑵.
注意:① 列出随机变量的所有可能取值;
② 求出随机变量的每一个值发生的概率.
4.离散型随机变量的均值与方差
⑴离散型随机变量的均值的概念
一般地,若离散型随机变量的概率分布为:
… …
… …
则称
为随机变量的均值或数学期望,数学期望简称期望.
⑵离散型随机变量的方差的概念
一般地,若离散型随机变量的概率分布列为:
… …
… …
则称
为随机变量的方差,有时也记为.称为随机变量的标准差.
【重要结论】
1.随机变量的线性关系
若是随机变量, 是常数, 则也是随机变量.
2.分布列性质的两个作用
(1)利用分布列中各事件概率之和为1可求参数的值.
(2)随机变量所取的值分别对应的事件是两两互斥的,利用这一点可以求相关事件的概率.
3.离散型随机变量的均值与方差的常用性质
⑴,其中为常数;
⑵,为常数,是随机变量;
⑶;
⑷;
⑸若相互独立,则;
⑹若,则的均值与方差分别为,.
1.【人教A版选择性必修三 7.2离散型随机变量及其分布列 例1 P59】已知离散型随机变量的分布列服从两点分布,满足,且,则 ( )
A. B. C. D.
2.【人教A版选择性必修三 习题7.3 第6题 P71】猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名,某嘉宾参加猜歌名节目,猜对每首歌名相互独立,猜对两首歌曲歌名的概率分别为,,且猜对两首歌曲歌名分别可得奖金为元,元规则规定:只有在猜对第一首歌名的情况下,才有资格猜第二首歌名.
若,,该嘉宾选择先猜,再猜,求他得到奖金的分布列及均值;
从得到奖金的均值的角度,该嘉宾应选择怎样的猜歌顺序,才能得更多的奖金?
【方法储备】
1.离散型随机变量的分布列的求解步骤:
第一步:确定的所有可能取值(),并明确每个取值代表的意义;
第二步:求出相应的概率 ();
第三步:写出分布列或列出分布列;
第四步;根据分布列的性质对结果进行检验.
注意:
⑴利用分布列中各事件概率之和为1可求参数的值及检查分布列的正确性.
⑵随机变量所取的值分别对应的事件是两两互斥的,利用这一点可以求随机变量在某个范围内的概率.
2.离散型随机变量分布列的常见类型及解题策略:
⑴与排列组合有关的分布列的求法.可由排列组合、概率知识求出概率,再求出分布列.
⑵与频率分布直方图有关的分布列的求法.可由频率估计概率,再求出分布列.
⑶与互斥事件有关的分布列的求法.弄清互斥事件的关系,利用概率公式求出概率,再列出分布列.
⑷与独立事件(或独立重复试验)有关的分布列的求法.先弄清独立事件的关系,求出各个概率,再列出分布列.
【典例精讲】
例1.(2023·广东省东莞市月考) 甲乙两人进行乒乓球比赛,经过以往的比赛分析,甲乙对阵时,若甲发球,则甲得分的概率为,若乙发球,则甲得分的概率为该局比赛中,甲乙依次轮换发球甲先发球,每人发两球后轮到对方进行发球.
求在前球中,甲领先的概率
球过后,双方战平,已知继续对战奇数球后,甲获得胜利获胜要求至少取得分并净胜对方分及以上设净胜分甲,乙的得分之差为,求的分布列.
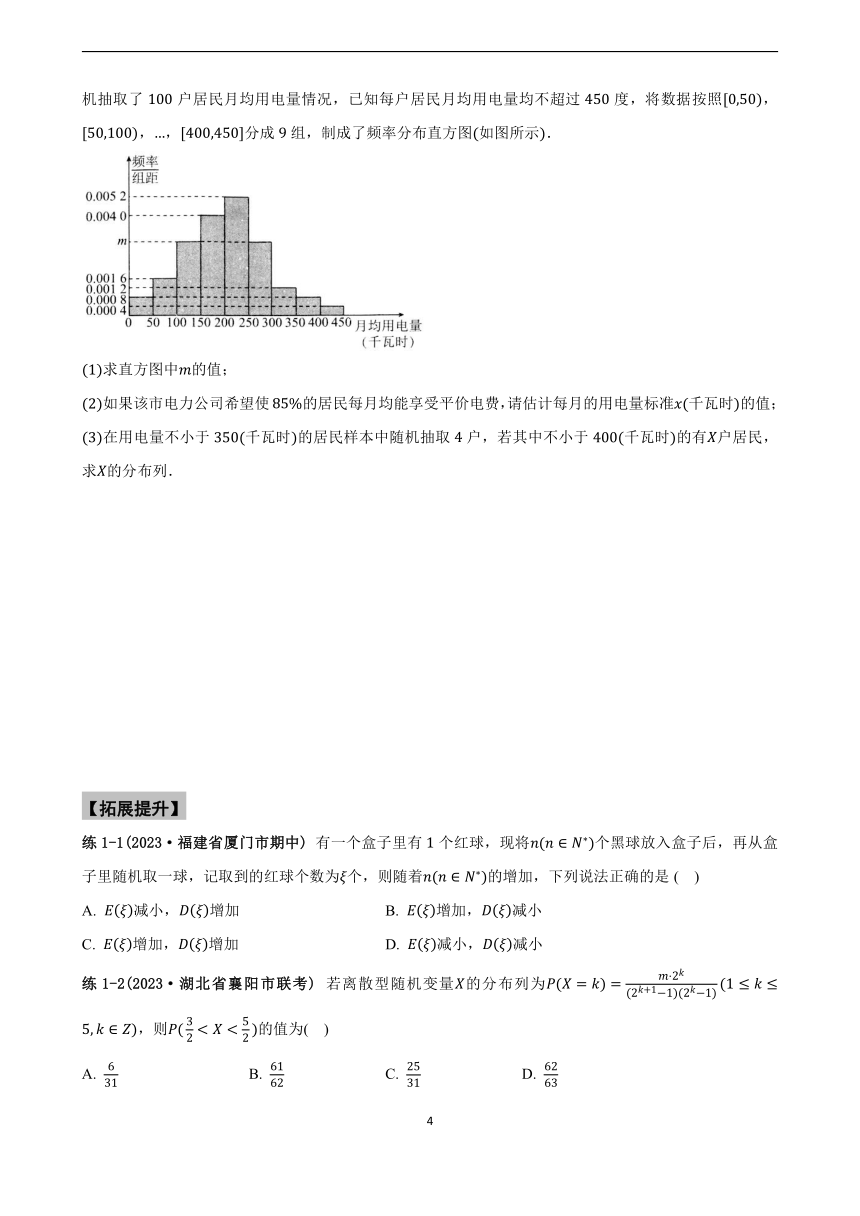
例2.(2023·江苏省淮安市模拟) 年月以来,多地限电的话题备受关注,广东省能源局和广东电网有限责任公司联合发布致全省电力用户有序用电、节约用电倡议书,目的在于引导大家如何有序节约用电.某市电力公司为了让居民节约用电,采用“阶梯电价”的方法计算电价,每户居民每月用电量不超过标准用电量千瓦时时,按平价计费,每月用电量超过标准电量千瓦时时,超过部分按议价计费.随机抽取了户居民月均用电量情况,已知每户居民月均用电量均不超过度,将数据按照,,,分成组,制成了频率分布直方图如图所示.
求直方图中的值;
如果该市电力公司希望使的居民每月均能享受平价电费,请估计每月的用电量标准千瓦时的值;
在用电量不小于千瓦时的居民样本中随机抽取户,若其中不小于千瓦时的有户居民,求的分布列.
【拓展提升】
练1-1(2023·福建省厦门市期中) 有一个盒子里有个红球,现将个黑球放入盒子后,再从盒子里随机取一球,记取到的红球个数为个,则随着的增加,下列说法正确的是( )
A. 减小,增加 B. 增加,减小
C. 增加,增加 D. 减小,减小
练1-2(2023·湖北省襄阳市联考) 若离散型随机变量的分布列为,则的值为( )
A. B. C. D.
练1-3(2023·辽宁省大连市月考) 甲、乙两人进行射击比赛,一局比赛中,先射击的一方最多可射击次,一旦未击中目标即停止,然后换另一方射击,一旦未击中目标或两方射击总次数达次均停止,本局比赛结束,各方击中目标的次数即为其本局比赛得分已知甲、乙每次射击击中目标的概率分别为和,两人的各次射击是否击中目标相互独立一局比赛中,若甲先射击.
求甲、乙得分相同的概率
设乙的得分为,求的分布列及数学期望.
【方法储备】
求离散型随机变量的期望与方差:
⑴求解离散型随机变量的分布列,利用离散型随机变量的期望与方差的公式,进行计算;
⑵二项分布的期望、方差可直接利用公式求解,但要注意模型及公式的正确性.
【典例精讲】
例3.(2023·山西省阳泉市模拟)年是中国共产主义青年团成立周年,某市团委决定举办一次共青团史知识抢答竞赛。抢到答题权并回答正确得分,回答错误对方得分。共抢答题,得分高者获胜甲、乙两名同学抢答过程中,甲抢到答题权的概率为,甲回答正确的概率为,乙回答正确的概率为。各题答题权的抢夺和答题正确率之间均相互独立。
求第一题甲得分高于乙得分的概率;
记甲得分为,求的分布列,期望和方差.
例4. (2023·辽宁省沈阳市模拟) 甲乙两人进行乒乓球比赛,现采用三局两胜的比赛制度,规定每一局比赛都没有平局必须分出胜负,且每一局甲赢的概率都是,随机变量表示最终的比赛局数,若,则的最大值是 ;的最值范围是 .
【拓展提升】
练2-1(2023·湖南省长沙市期末) 某校为了合理配置校本课程资源,教务部门对学生们进行了问卷调查,据统计,其中的学生计划只选择校本课程一,另外的学生计划既选择校本课程一又选择校本课程二每位学生若只选择校本课程一,则记分若既选择校本课程一又选择校本课程二,则记分,假设每位选择校本课程一的学生是否计划选择校本课程二相互独立,视频率为概率.
从学生中随机抽取人,记这人的合计得分为,求的分布列和数学期望
从学生中随机抽取人,记这人的合计得分恰为分的概率为,求
练2-2(2023·山东省青岛市入学测试) 为弘扬中华优秀传统文化,营造良好的文化氛围,某高中校团委组织非毕业年级开展了“我们的元宵节”主题知识竞答活动,该活动有个人赛和团体赛,每人只能参加其中的一项,根据各位学生答题情况,获奖学生人数统计如下:
奖项组别 个人赛 团体赛获奖
一等奖 二等奖 三等奖
高一
高二
Ⅰ从获奖学生中随机抽取人,若已知抽到的学生获得一等奖,求抽到的学生来自高一的概率
Ⅱ从高一和高二获奖者中各随机抽取人,以表示这人中团体赛获奖的人数,
求的分布列和数学期望
Ⅲ从获奖学生中随机抽取人,设这人中来自高一的人数为,来自高二的人数为,试判断与的大小关系结论不要求证明
【方法储备】
随机变量的均值和方差从整体和全局上刻画了随机变量,是生产实际中用于方案取舍的重要理论依据.一般先比较均值,若均值相同,再用方差来决定.
⑴当期望不同时,两个随机变量取值水平可见分歧,可对问题作出判断.
⑵若两个随机变量期望相同或相差不大,则可通过分析两变量的方差来研究随机变量的离散程度或者稳定程度,进而进行决策.
⑶实际应用中是方差(期望)大了好还是小了好,要根据这组数据反应的实际问题来判断.
【典例精讲】
例5.(2023·四川省成都市月考) 有甲、乙两家公司都需要招聘求职者,这两家公司的聘用信息如表所示.
甲公司 乙公司
职位 职位
月薪千元 月薪千元
获得相应职位概率 获得相应职位概率
若一人去应聘甲公司的职位,另一人去应聘乙公司的职位,记这两人被录用的人数和为,求的分布列.
若小方和小芳分别被甲、乙两家公司录用,求小方月薪高于小芳月薪的概率.
根据甲、乙两家公司的聘用信息,如果你是求职者,你会选择哪一家公司?说明理由.
例6.(2023·浙江省金华市期中) 某景区有一个自愿消费的项目,在某特色景点入口处,工作人员会为每位游客拍一张与景点的合影,参观后,在景点出口处会将刚拍下的照片打印出来,游客可自由选择是否带走照片若带走照片则需支付元,没有被带走的照片会收集起来统一销毁该项目运营一段时间后,统计出平均只有三成的游客会选择带走照片为改善运营状况,该项目组就照片收费与游客消费意愿的关系做了市场调研,发现价格与消费意愿有较强的线性相关性统计出在原有的基础上,价格每下调元,游客选择带走照片的概率平均增加假设平均每天约有人参观该特色景点,每张照片的综合成本为元,每个游客是否选择带走照片相互独立.
若调整为支付元就可带走照片,该项目每天的平均利润比调整前多还是少
要使每天的平均利润达到最大值,应如何定价
【拓展提升】
练3-1(2023·广东省汕头市模拟) 从年起,全国高考数学加入了新题型多选题,每个小题给出的四个选择中有多项是正确的,其中回答错误得分,部分正确得分,完全正确得分,小明根据以前做过的多项选择题统计得到,多选题有两个选项的概率为,有三个选项的概率为其中.
若,小明对某个多项选择题完全不会,决定随机选择一个选项,求小明得分的概率
在某个多项选择题中,小明发现选项A正确,选项B错误,下面小明有三种不同策略:
Ⅰ选择,再从剩下的,选项中随机选择一个,小明该题的得分为
Ⅱ选择,小明该题的得分为
Ⅲ只选择,小明该题的得分为
在变化时,根据该题得分的期望来帮助小明分析该选择哪个策略.
练3-2(2023·江苏省南通市期中) 某学校组织“一带一路”知识竞赛,有,两类问题,每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误,则该同学比赛结束;若回答正确,则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.类问题中的每个问题回答正确得分,否则得分;类问题中的每个问题回答正确得分,否则得分.已知学生甲能正确回答类问题的概率为,能正确回答类问题的概率为,且能正确回答问题的概率与回答次序无关.
若学生甲先回答类问题,,,,,记为学生甲的累计得分,求的分布列和数学期望.
从下面的两组条件中选择一组作为已知条件.学生甲应选择先回答哪类问题,使得累计得分的数学期望最大?并证明你的结论.①,;②,.
1.(2023·湖北省黄冈市月考) 设随机变量,当正整数很大,很小,不大时,的分布接近泊松分布,即现需个正品元件,该元件的次品率为,若要有以上的概率购得个正品,则至少需购买的元件个数为已知( )
A. B. C. D.
2.(2023·江西省宜春市入学测试) 一对夫妻计划进行为期天的自驾游.已知两人均能驾驶车辆,且约定:①在任意一天的旅途中,全天只由其中一人驾车,另一人休息;②若前一天由丈夫驾车,则下一天继续由丈夫驾车的概率为,由妻子驾车的概率为;③妻子不能连续两天驾车.已知第一天夫妻双方驾车的概率均为.
求在刚开始的三天中,妻子驾车天数的概率分布列和数学期望;
设在第天时,由丈夫驾车的概率为,求数列的通项公式.
3.(2023·河北省模拟题) 第届世界大学生夏季运动会将于今年在我国成都举行.某体校田径队正在积极备战,考核设有米、米和米三个项目,需要选手依次完成考核,成绩合格后的积分分别记为,和,,,,总成绩为累计积分和.考核规定:项目考核逐级进阶,即选手只有在低一级里程项目考核合格后,才能进行下一级较高里程项目的考核,否则考核终止.对于米和米项目,每个项目选手必须考核次,且全部达标才算合格;对于米项目,选手必须考核次,但只要达标次及以上就算合格.已知选手甲三个项目的达标率依次为,,,选手乙三个项目的达标率依次为,,,每次考核是否达标相互独立.
用表示选手甲考核积分的总成绩,求的分布列和数学期望;
证明:无论,和取何值,选手甲考核积分总成绩的数学期望值都大于选手乙考核积分总成绩的数学期望值.
【答案解析】
1.【人教A版选择性必修三 7.2离散型随机变量及其分布列 例1 P59】
解:由题意,,
又,所以,解得或,
又,故,,
故.故选C.
2.【人教A版选择性必修三 习题7.3 第6题 P71】
解:的可能取值为,,,
,
,
,
所以分布列为
;
设先猜,再猜得到奖金为,先猜,再猜得到奖金为,
则的可能取值为,,,的可能取值为,,,
,,,
,,,
,
,
,
当时,即,即,先猜与先猜一样;
当时,即,即,应先猜;
当时,即,即,应先猜.
例1.解:甲与乙的比分是的概率为,
比分是的概率为,
故前球中,甲领先的概率;
依题意,接下来由甲先发球继续对战奇数球后,甲获得胜利,则甲或获胜,
即在接下来的比赛中,甲乙的比分为或,且最后一球均为甲获胜.
记比分为为事件,则
,
记比分为为事件,即前球中,乙获胜两球,期间甲发球次,乙发球两次,
,
故甲依题意获胜的概率为,
的所有可能取值为,,
由条件概率有,,
故的分布列为
例2.解:由题得,
解得.
月均用电量小于千瓦时的居民家庭所占百分比为
,
即的居民家庭月均用电量小于千瓦时,
同理,的居民月均用电量小于千瓦时,
故,则,
解得千瓦时.
在样本中用电量不小于千瓦时的居民共有户,
用电量不小于千瓦时的居民共有户,
由题意随机变量可取,,,
,
,
,
所以随机变量的分布列为:
练1-1.解:由题意可得,取到红球个数服从两点分布,其中,
则随着的增大,减小,
,
设,
求导可得,当时,,故在上单调递减,
则当时,随着的增大而减少.
故选:.
练1-2.解:由题可知,
则由离散型随机变量分布列的性质可得
,
解得,
故.
故选A.
练1-3.解:甲、乙各得分的概率;
甲、乙各得分的概率;
甲、乙各得分的概率;
故两人得分相同的概率为.
由题意知的所有可能取值分别为,,,,,
因为甲最多射击次,所以表示乙第一次射击就未击中目标,其概率与甲的得分无关,
故,
同理,
时,考虑甲射击次和少于次两种情况,
,
同理,,
的分布列为:
.
例3.解:设事件甲抢到答题权并回答正确,乙抢到答题权并回答错误
,.
第一题甲得分高于乙得分的概率
设甲得分为,
可能的取值为,,,,
由知
,
,
例4.解:由已知条件可得,的所有可能取值为,,
,
,
故E,
,,
故E的最大值是,
,
令,
,,
.
故答案为;.
练2-1.解:由题意知,每位学生计划不选择校本课程二的概率为,
选择校本课程二的概率为,则的可能取值为,,,,
,,
,,
所以的分布列如下表所示:
所以.
因为这人的合计得分为分,则其中只有人计划选择校本课程二,
所以,
设,
则,
由两式相减得,
即,
所以
练2-2.解:Ⅰ记“任取名学生,该生获得一等奖”为事件,
记“任取名学生,该生为高一学生”为事件,
,,
;
Ⅱ由已知可得,的可能取值为,,
,
,
,
的分布列为
Ⅲ,
理由:,,
例5.解:,,,
则,,,
所以的分布列为
小方月薪高于小芳月薪的概率:
入职甲公司,月薪的期望为,
方差,
入职乙公司,月薪的期望为,
方差,
乙公司月薪高于甲公司的概率为,
即,
即两家公司月薪的期望相同,但甲公司月薪的波动性小,乙公司的月薪波动性更大,且甲公司月薪高于乙公司的月薪概率更大,故选甲公司.
例6.解:当收费为元时,照片被带走的概率为,不被带走的概率为设每个游客的利润为元,则是随机变量,其分布列为:
元,
故个游客的平均利润为元,
当收费为元时,照片被带走的概率为,不被带走的概率为,
设每个游客的利润为元,则是随机变量,其分布列为:
元,
故个游客的平均利润为元,
该项目每天的平均利润比调整前多元;
设降价元,则,照片被带走的概率为,不被带走的概率为,
设每个游客的利润为元,则是随机变量,其分布列为:
,
当时,有最大值元,
当定价为元时,日平均利润的最大值为元.
练3-1.解:若答案是两个选项,所有的可能有:,,,,,共种,
则小明只选一个得分的概率为:;
答案是三个选项,所有的可能有:有,,,,共种,
则小明只选一个得分的概率为:;
故小明得分的概率为;
选策略,则小明得分为的分布列为:
得分的期望为;
选策略Ⅱ,则小明得分为的分布列为:
得分的期望为;
选策略Ⅲ,得分为,则,
当,
此时,,故此时选择策略,
当时,,最大,此时选择策略Ⅱ,
当时,策略,Ⅱ概率一样,都可以.
练3-2.解:由题意得的可能取值为,,.
,
,
,
分布列如下表:
则的数学期望.
如果选择条件①.
若甲同学选择先回答类问题,得到对应的分布列为
若甲同学选择先回答类问题,得到对应的分布列为
,
所以甲同学先回答类问题的期望大.
评分标准同上如果选择条件②.
若甲同学选择先回答类问题,得到对应的分布列为
若甲同学选择先回答类问题,得到对应的分布列为
,,
所以甲同学先回答类问题的期望大.
1.解:记随机变量为购买个元件后的次品数.
由题意,此时可看成泊松分布,则,记,
则,由于很小,故大致有,
分别计算,,,,左边约等于,,,,
故,即.
则至少需购买的元件个数为.
故选D.
2.解:设在刚开始的三天中,妻子驾车的天数为随机变量,则可能取值为,,,
则,
,
,
因此的分布列为:
所以.
设在第天时,由丈夫驾车的概率为.
因为第天夫妻双方驾车的概率均为,
所以第天由丈夫驾车的概率.
因为第天和第天都由丈夫驾车的概率为
第天由妻子驾车,第天由丈夫驾车的概率为,
所以第天由丈夫驾车的概率.
因为妻子不能连续两天驾车,所以第天由妻子驾车,
则第天必由丈夫驾车,第天由丈夫驾车,其概率为
若第天由丈夫驾车,则第天由丈夫驾车的概率为,
所以第天由丈夫驾车的概率,
因此.
又因为,所以数列是首项为,公比为的等比数列,
因此
.
3.解:选手甲考核积分的总成绩的所有可能取值为,,,.
,
.
所以的分布列为
所以数学期期.
证明:记选手乙考核积分的总成绩为,
则所有可能的取值为,,,.
,,
,
.
所以的分布列为
所以数学期望.
所以,
所以,即无论,和取何值,选手甲考核积分总成绩的数学期望都大于选手乙考核积分总成绩的数学期望.
2
1.离散型随机变量
一般地,对于随机试验样本空间中的每个样本点都有唯一的实数与之对应,我们称为随机变量.
表示:用大写英文字母表示随机变量,如;用小写英文字母表示随机变量的取值,如.
2.离散型随机变量的分布列
一般地,设离散型随机变量的可能取值为,我们称取每一个值的概率
为的概率分布列,简称分布列.
与函数的表示方法类似,离散型随机变量的分布列也可以用表格表示:
… …
… …
3.离散型随机变量的分布列的性质
⑴;
⑵.
注意:① 列出随机变量的所有可能取值;
② 求出随机变量的每一个值发生的概率.
4.离散型随机变量的均值与方差
⑴离散型随机变量的均值的概念
一般地,若离散型随机变量的概率分布为:
… …
… …
则称
为随机变量的均值或数学期望,数学期望简称期望.
⑵离散型随机变量的方差的概念
一般地,若离散型随机变量的概率分布列为:
… …
… …
则称
为随机变量的方差,有时也记为.称为随机变量的标准差.
【重要结论】
1.随机变量的线性关系
若是随机变量, 是常数, 则也是随机变量.
2.分布列性质的两个作用
(1)利用分布列中各事件概率之和为1可求参数的值.
(2)随机变量所取的值分别对应的事件是两两互斥的,利用这一点可以求相关事件的概率.
3.离散型随机变量的均值与方差的常用性质
⑴,其中为常数;
⑵,为常数,是随机变量;
⑶;
⑷;
⑸若相互独立,则;
⑹若,则的均值与方差分别为,.
1.【人教A版选择性必修三 7.2离散型随机变量及其分布列 例1 P59】已知离散型随机变量的分布列服从两点分布,满足,且,则 ( )
A. B. C. D.
2.【人教A版选择性必修三 习题7.3 第6题 P71】猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名,某嘉宾参加猜歌名节目,猜对每首歌名相互独立,猜对两首歌曲歌名的概率分别为,,且猜对两首歌曲歌名分别可得奖金为元,元规则规定:只有在猜对第一首歌名的情况下,才有资格猜第二首歌名.
若,,该嘉宾选择先猜,再猜,求他得到奖金的分布列及均值;
从得到奖金的均值的角度,该嘉宾应选择怎样的猜歌顺序,才能得更多的奖金?
【方法储备】
1.离散型随机变量的分布列的求解步骤:
第一步:确定的所有可能取值(),并明确每个取值代表的意义;
第二步:求出相应的概率 ();
第三步:写出分布列或列出分布列;
第四步;根据分布列的性质对结果进行检验.
注意:
⑴利用分布列中各事件概率之和为1可求参数的值及检查分布列的正确性.
⑵随机变量所取的值分别对应的事件是两两互斥的,利用这一点可以求随机变量在某个范围内的概率.
2.离散型随机变量分布列的常见类型及解题策略:
⑴与排列组合有关的分布列的求法.可由排列组合、概率知识求出概率,再求出分布列.
⑵与频率分布直方图有关的分布列的求法.可由频率估计概率,再求出分布列.
⑶与互斥事件有关的分布列的求法.弄清互斥事件的关系,利用概率公式求出概率,再列出分布列.
⑷与独立事件(或独立重复试验)有关的分布列的求法.先弄清独立事件的关系,求出各个概率,再列出分布列.
【典例精讲】
例1.(2023·广东省东莞市月考) 甲乙两人进行乒乓球比赛,经过以往的比赛分析,甲乙对阵时,若甲发球,则甲得分的概率为,若乙发球,则甲得分的概率为该局比赛中,甲乙依次轮换发球甲先发球,每人发两球后轮到对方进行发球.
求在前球中,甲领先的概率
球过后,双方战平,已知继续对战奇数球后,甲获得胜利获胜要求至少取得分并净胜对方分及以上设净胜分甲,乙的得分之差为,求的分布列.
例2.(2023·江苏省淮安市模拟) 年月以来,多地限电的话题备受关注,广东省能源局和广东电网有限责任公司联合发布致全省电力用户有序用电、节约用电倡议书,目的在于引导大家如何有序节约用电.某市电力公司为了让居民节约用电,采用“阶梯电价”的方法计算电价,每户居民每月用电量不超过标准用电量千瓦时时,按平价计费,每月用电量超过标准电量千瓦时时,超过部分按议价计费.随机抽取了户居民月均用电量情况,已知每户居民月均用电量均不超过度,将数据按照,,,分成组,制成了频率分布直方图如图所示.
求直方图中的值;
如果该市电力公司希望使的居民每月均能享受平价电费,请估计每月的用电量标准千瓦时的值;
在用电量不小于千瓦时的居民样本中随机抽取户,若其中不小于千瓦时的有户居民,求的分布列.
【拓展提升】
练1-1(2023·福建省厦门市期中) 有一个盒子里有个红球,现将个黑球放入盒子后,再从盒子里随机取一球,记取到的红球个数为个,则随着的增加,下列说法正确的是( )
A. 减小,增加 B. 增加,减小
C. 增加,增加 D. 减小,减小
练1-2(2023·湖北省襄阳市联考) 若离散型随机变量的分布列为,则的值为( )
A. B. C. D.
练1-3(2023·辽宁省大连市月考) 甲、乙两人进行射击比赛,一局比赛中,先射击的一方最多可射击次,一旦未击中目标即停止,然后换另一方射击,一旦未击中目标或两方射击总次数达次均停止,本局比赛结束,各方击中目标的次数即为其本局比赛得分已知甲、乙每次射击击中目标的概率分别为和,两人的各次射击是否击中目标相互独立一局比赛中,若甲先射击.
求甲、乙得分相同的概率
设乙的得分为,求的分布列及数学期望.
【方法储备】
求离散型随机变量的期望与方差:
⑴求解离散型随机变量的分布列,利用离散型随机变量的期望与方差的公式,进行计算;
⑵二项分布的期望、方差可直接利用公式求解,但要注意模型及公式的正确性.
【典例精讲】
例3.(2023·山西省阳泉市模拟)年是中国共产主义青年团成立周年,某市团委决定举办一次共青团史知识抢答竞赛。抢到答题权并回答正确得分,回答错误对方得分。共抢答题,得分高者获胜甲、乙两名同学抢答过程中,甲抢到答题权的概率为,甲回答正确的概率为,乙回答正确的概率为。各题答题权的抢夺和答题正确率之间均相互独立。
求第一题甲得分高于乙得分的概率;
记甲得分为,求的分布列,期望和方差.
例4. (2023·辽宁省沈阳市模拟) 甲乙两人进行乒乓球比赛,现采用三局两胜的比赛制度,规定每一局比赛都没有平局必须分出胜负,且每一局甲赢的概率都是,随机变量表示最终的比赛局数,若,则的最大值是 ;的最值范围是 .
【拓展提升】
练2-1(2023·湖南省长沙市期末) 某校为了合理配置校本课程资源,教务部门对学生们进行了问卷调查,据统计,其中的学生计划只选择校本课程一,另外的学生计划既选择校本课程一又选择校本课程二每位学生若只选择校本课程一,则记分若既选择校本课程一又选择校本课程二,则记分,假设每位选择校本课程一的学生是否计划选择校本课程二相互独立,视频率为概率.
从学生中随机抽取人,记这人的合计得分为,求的分布列和数学期望
从学生中随机抽取人,记这人的合计得分恰为分的概率为,求
练2-2(2023·山东省青岛市入学测试) 为弘扬中华优秀传统文化,营造良好的文化氛围,某高中校团委组织非毕业年级开展了“我们的元宵节”主题知识竞答活动,该活动有个人赛和团体赛,每人只能参加其中的一项,根据各位学生答题情况,获奖学生人数统计如下:
奖项组别 个人赛 团体赛获奖
一等奖 二等奖 三等奖
高一
高二
Ⅰ从获奖学生中随机抽取人,若已知抽到的学生获得一等奖,求抽到的学生来自高一的概率
Ⅱ从高一和高二获奖者中各随机抽取人,以表示这人中团体赛获奖的人数,
求的分布列和数学期望
Ⅲ从获奖学生中随机抽取人,设这人中来自高一的人数为,来自高二的人数为,试判断与的大小关系结论不要求证明
【方法储备】
随机变量的均值和方差从整体和全局上刻画了随机变量,是生产实际中用于方案取舍的重要理论依据.一般先比较均值,若均值相同,再用方差来决定.
⑴当期望不同时,两个随机变量取值水平可见分歧,可对问题作出判断.
⑵若两个随机变量期望相同或相差不大,则可通过分析两变量的方差来研究随机变量的离散程度或者稳定程度,进而进行决策.
⑶实际应用中是方差(期望)大了好还是小了好,要根据这组数据反应的实际问题来判断.
【典例精讲】
例5.(2023·四川省成都市月考) 有甲、乙两家公司都需要招聘求职者,这两家公司的聘用信息如表所示.
甲公司 乙公司
职位 职位
月薪千元 月薪千元
获得相应职位概率 获得相应职位概率
若一人去应聘甲公司的职位,另一人去应聘乙公司的职位,记这两人被录用的人数和为,求的分布列.
若小方和小芳分别被甲、乙两家公司录用,求小方月薪高于小芳月薪的概率.
根据甲、乙两家公司的聘用信息,如果你是求职者,你会选择哪一家公司?说明理由.
例6.(2023·浙江省金华市期中) 某景区有一个自愿消费的项目,在某特色景点入口处,工作人员会为每位游客拍一张与景点的合影,参观后,在景点出口处会将刚拍下的照片打印出来,游客可自由选择是否带走照片若带走照片则需支付元,没有被带走的照片会收集起来统一销毁该项目运营一段时间后,统计出平均只有三成的游客会选择带走照片为改善运营状况,该项目组就照片收费与游客消费意愿的关系做了市场调研,发现价格与消费意愿有较强的线性相关性统计出在原有的基础上,价格每下调元,游客选择带走照片的概率平均增加假设平均每天约有人参观该特色景点,每张照片的综合成本为元,每个游客是否选择带走照片相互独立.
若调整为支付元就可带走照片,该项目每天的平均利润比调整前多还是少
要使每天的平均利润达到最大值,应如何定价
【拓展提升】
练3-1(2023·广东省汕头市模拟) 从年起,全国高考数学加入了新题型多选题,每个小题给出的四个选择中有多项是正确的,其中回答错误得分,部分正确得分,完全正确得分,小明根据以前做过的多项选择题统计得到,多选题有两个选项的概率为,有三个选项的概率为其中.
若,小明对某个多项选择题完全不会,决定随机选择一个选项,求小明得分的概率
在某个多项选择题中,小明发现选项A正确,选项B错误,下面小明有三种不同策略:
Ⅰ选择,再从剩下的,选项中随机选择一个,小明该题的得分为
Ⅱ选择,小明该题的得分为
Ⅲ只选择,小明该题的得分为
在变化时,根据该题得分的期望来帮助小明分析该选择哪个策略.
练3-2(2023·江苏省南通市期中) 某学校组织“一带一路”知识竞赛,有,两类问题,每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误,则该同学比赛结束;若回答正确,则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.类问题中的每个问题回答正确得分,否则得分;类问题中的每个问题回答正确得分,否则得分.已知学生甲能正确回答类问题的概率为,能正确回答类问题的概率为,且能正确回答问题的概率与回答次序无关.
若学生甲先回答类问题,,,,,记为学生甲的累计得分,求的分布列和数学期望.
从下面的两组条件中选择一组作为已知条件.学生甲应选择先回答哪类问题,使得累计得分的数学期望最大?并证明你的结论.①,;②,.
1.(2023·湖北省黄冈市月考) 设随机变量,当正整数很大,很小,不大时,的分布接近泊松分布,即现需个正品元件,该元件的次品率为,若要有以上的概率购得个正品,则至少需购买的元件个数为已知( )
A. B. C. D.
2.(2023·江西省宜春市入学测试) 一对夫妻计划进行为期天的自驾游.已知两人均能驾驶车辆,且约定:①在任意一天的旅途中,全天只由其中一人驾车,另一人休息;②若前一天由丈夫驾车,则下一天继续由丈夫驾车的概率为,由妻子驾车的概率为;③妻子不能连续两天驾车.已知第一天夫妻双方驾车的概率均为.
求在刚开始的三天中,妻子驾车天数的概率分布列和数学期望;
设在第天时,由丈夫驾车的概率为,求数列的通项公式.
3.(2023·河北省模拟题) 第届世界大学生夏季运动会将于今年在我国成都举行.某体校田径队正在积极备战,考核设有米、米和米三个项目,需要选手依次完成考核,成绩合格后的积分分别记为,和,,,,总成绩为累计积分和.考核规定:项目考核逐级进阶,即选手只有在低一级里程项目考核合格后,才能进行下一级较高里程项目的考核,否则考核终止.对于米和米项目,每个项目选手必须考核次,且全部达标才算合格;对于米项目,选手必须考核次,但只要达标次及以上就算合格.已知选手甲三个项目的达标率依次为,,,选手乙三个项目的达标率依次为,,,每次考核是否达标相互独立.
用表示选手甲考核积分的总成绩,求的分布列和数学期望;
证明:无论,和取何值,选手甲考核积分总成绩的数学期望值都大于选手乙考核积分总成绩的数学期望值.
【答案解析】
1.【人教A版选择性必修三 7.2离散型随机变量及其分布列 例1 P59】
解:由题意,,
又,所以,解得或,
又,故,,
故.故选C.
2.【人教A版选择性必修三 习题7.3 第6题 P71】
解:的可能取值为,,,
,
,
,
所以分布列为
;
设先猜,再猜得到奖金为,先猜,再猜得到奖金为,
则的可能取值为,,,的可能取值为,,,
,,,
,,,
,
,
,
当时,即,即,先猜与先猜一样;
当时,即,即,应先猜;
当时,即,即,应先猜.
例1.解:甲与乙的比分是的概率为,
比分是的概率为,
故前球中,甲领先的概率;
依题意,接下来由甲先发球继续对战奇数球后,甲获得胜利,则甲或获胜,
即在接下来的比赛中,甲乙的比分为或,且最后一球均为甲获胜.
记比分为为事件,则
,
记比分为为事件,即前球中,乙获胜两球,期间甲发球次,乙发球两次,
,
故甲依题意获胜的概率为,
的所有可能取值为,,
由条件概率有,,
故的分布列为
例2.解:由题得,
解得.
月均用电量小于千瓦时的居民家庭所占百分比为
,
即的居民家庭月均用电量小于千瓦时,
同理,的居民月均用电量小于千瓦时,
故,则,
解得千瓦时.
在样本中用电量不小于千瓦时的居民共有户,
用电量不小于千瓦时的居民共有户,
由题意随机变量可取,,,
,
,
,
所以随机变量的分布列为:
练1-1.解:由题意可得,取到红球个数服从两点分布,其中,
则随着的增大,减小,
,
设,
求导可得,当时,,故在上单调递减,
则当时,随着的增大而减少.
故选:.
练1-2.解:由题可知,
则由离散型随机变量分布列的性质可得
,
解得,
故.
故选A.
练1-3.解:甲、乙各得分的概率;
甲、乙各得分的概率;
甲、乙各得分的概率;
故两人得分相同的概率为.
由题意知的所有可能取值分别为,,,,,
因为甲最多射击次,所以表示乙第一次射击就未击中目标,其概率与甲的得分无关,
故,
同理,
时,考虑甲射击次和少于次两种情况,
,
同理,,
的分布列为:
.
例3.解:设事件甲抢到答题权并回答正确,乙抢到答题权并回答错误
,.
第一题甲得分高于乙得分的概率
设甲得分为,
可能的取值为,,,,
由知
,
,
例4.解:由已知条件可得,的所有可能取值为,,
,
,
故E,
,,
故E的最大值是,
,
令,
,,
.
故答案为;.
练2-1.解:由题意知,每位学生计划不选择校本课程二的概率为,
选择校本课程二的概率为,则的可能取值为,,,,
,,
,,
所以的分布列如下表所示:
所以.
因为这人的合计得分为分,则其中只有人计划选择校本课程二,
所以,
设,
则,
由两式相减得,
即,
所以
练2-2.解:Ⅰ记“任取名学生,该生获得一等奖”为事件,
记“任取名学生,该生为高一学生”为事件,
,,
;
Ⅱ由已知可得,的可能取值为,,
,
,
,
的分布列为
Ⅲ,
理由:,,
例5.解:,,,
则,,,
所以的分布列为
小方月薪高于小芳月薪的概率:
入职甲公司,月薪的期望为,
方差,
入职乙公司,月薪的期望为,
方差,
乙公司月薪高于甲公司的概率为,
即,
即两家公司月薪的期望相同,但甲公司月薪的波动性小,乙公司的月薪波动性更大,且甲公司月薪高于乙公司的月薪概率更大,故选甲公司.
例6.解:当收费为元时,照片被带走的概率为,不被带走的概率为设每个游客的利润为元,则是随机变量,其分布列为:
元,
故个游客的平均利润为元,
当收费为元时,照片被带走的概率为,不被带走的概率为,
设每个游客的利润为元,则是随机变量,其分布列为:
元,
故个游客的平均利润为元,
该项目每天的平均利润比调整前多元;
设降价元,则,照片被带走的概率为,不被带走的概率为,
设每个游客的利润为元,则是随机变量,其分布列为:
,
当时,有最大值元,
当定价为元时,日平均利润的最大值为元.
练3-1.解:若答案是两个选项,所有的可能有:,,,,,共种,
则小明只选一个得分的概率为:;
答案是三个选项,所有的可能有:有,,,,共种,
则小明只选一个得分的概率为:;
故小明得分的概率为;
选策略,则小明得分为的分布列为:
得分的期望为;
选策略Ⅱ,则小明得分为的分布列为:
得分的期望为;
选策略Ⅲ,得分为,则,
当,
此时,,故此时选择策略,
当时,,最大,此时选择策略Ⅱ,
当时,策略,Ⅱ概率一样,都可以.
练3-2.解:由题意得的可能取值为,,.
,
,
,
分布列如下表:
则的数学期望.
如果选择条件①.
若甲同学选择先回答类问题,得到对应的分布列为
若甲同学选择先回答类问题,得到对应的分布列为
,
所以甲同学先回答类问题的期望大.
评分标准同上如果选择条件②.
若甲同学选择先回答类问题,得到对应的分布列为
若甲同学选择先回答类问题,得到对应的分布列为
,,
所以甲同学先回答类问题的期望大.
1.解:记随机变量为购买个元件后的次品数.
由题意,此时可看成泊松分布,则,记,
则,由于很小,故大致有,
分别计算,,,,左边约等于,,,,
故,即.
则至少需购买的元件个数为.
故选D.
2.解:设在刚开始的三天中,妻子驾车的天数为随机变量,则可能取值为,,,
则,
,
,
因此的分布列为:
所以.
设在第天时,由丈夫驾车的概率为.
因为第天夫妻双方驾车的概率均为,
所以第天由丈夫驾车的概率.
因为第天和第天都由丈夫驾车的概率为
第天由妻子驾车,第天由丈夫驾车的概率为,
所以第天由丈夫驾车的概率.
因为妻子不能连续两天驾车,所以第天由妻子驾车,
则第天必由丈夫驾车,第天由丈夫驾车,其概率为
若第天由丈夫驾车,则第天由丈夫驾车的概率为,
所以第天由丈夫驾车的概率,
因此.
又因为,所以数列是首项为,公比为的等比数列,
因此
.
3.解:选手甲考核积分的总成绩的所有可能取值为,,,.
,
.
所以的分布列为
所以数学期期.
证明:记选手乙考核积分的总成绩为,
则所有可能的取值为,,,.
,,
,
.
所以的分布列为
所以数学期望.
所以,
所以,即无论,和取何值,选手甲考核积分总成绩的数学期望都大于选手乙考核积分总成绩的数学期望.
2
同课章节目录
