数学六年级下鲁教版7.1两条直线的位置关系课件
文档属性
| 名称 | 数学六年级下鲁教版7.1两条直线的位置关系课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 210.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-24 07:17:21 | ||
图片预览


文档简介
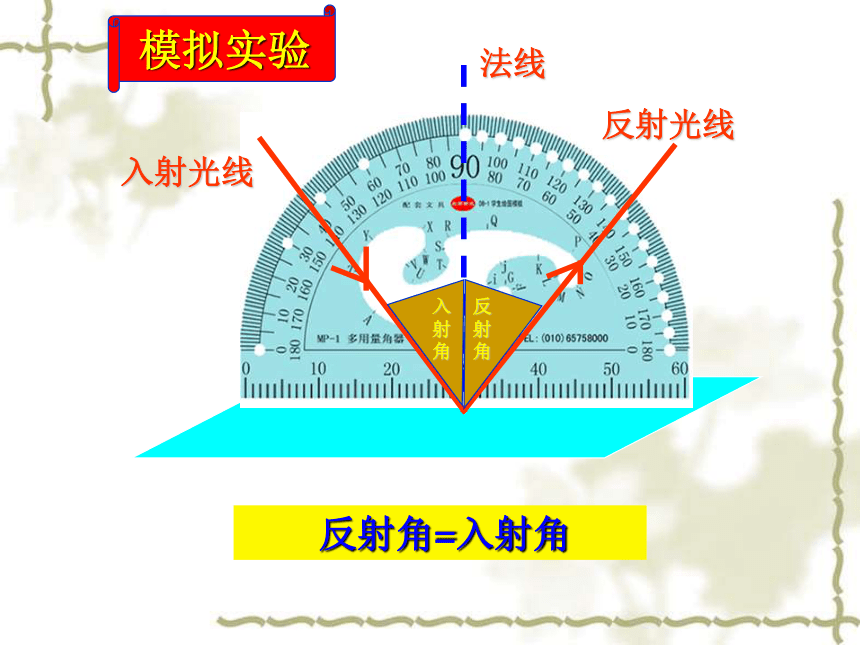
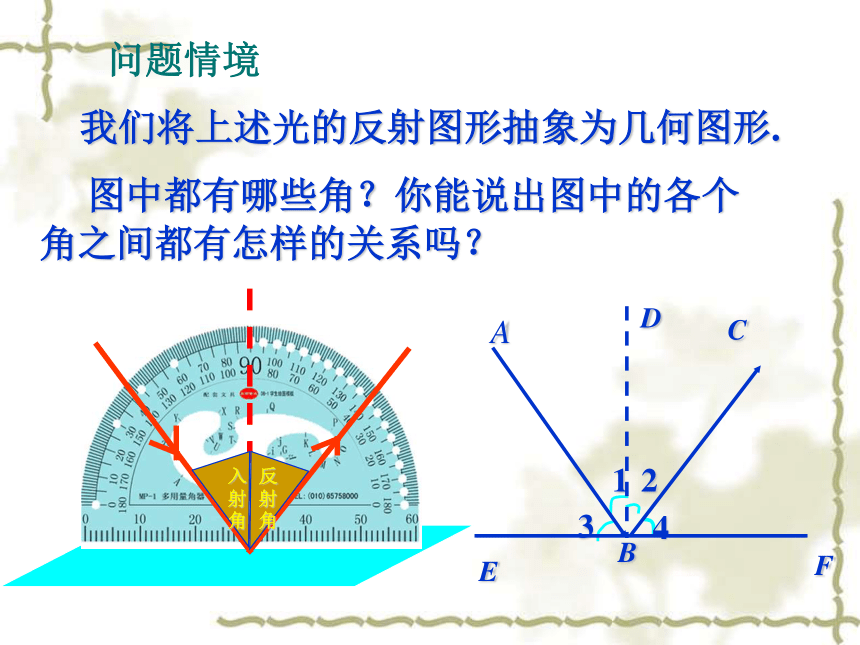
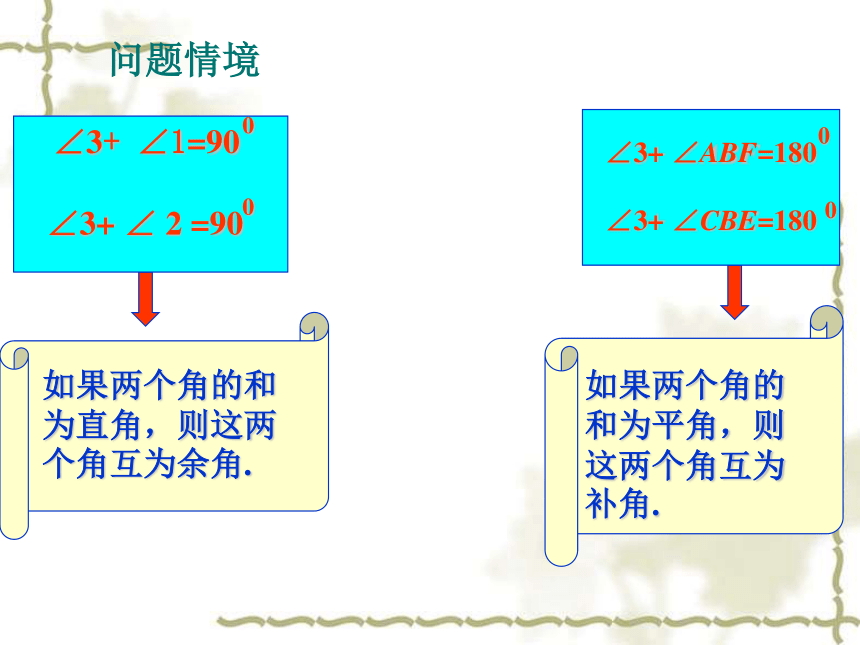
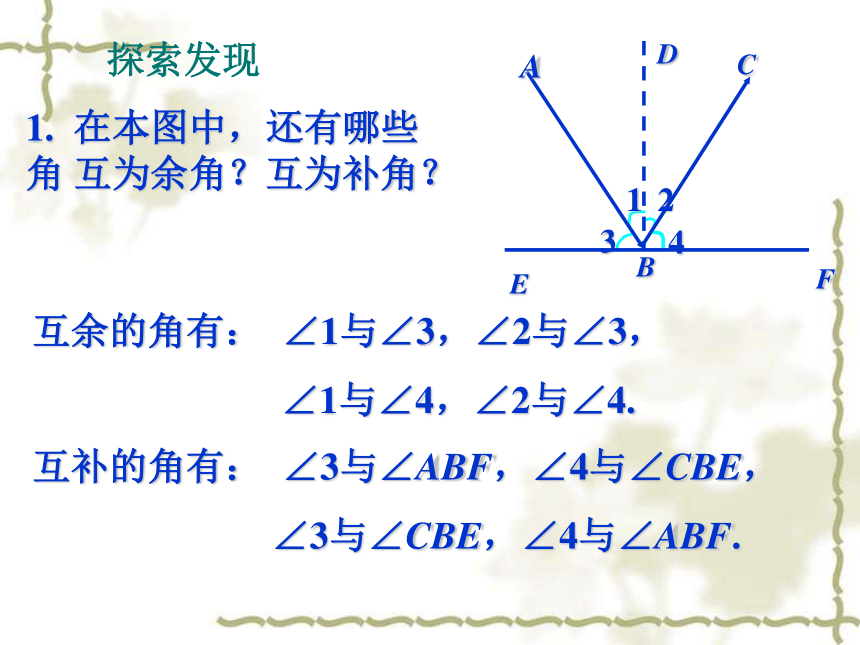
课件12张PPT。7.1 两条直线的位置关系(1) 生活中处处可见道路、房屋、山川、桥梁.在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线. 在这一章里,我们将发现相交线和平行线的一些特征,并探索两条直线平行的条件.我们还将利用圆规和没有刻度的直尺,尝试着作一些美丽的图案!问题情境 反射角=入射角入射角反射角入射光线反射光线法线模拟实验我们将上述光的反射图形抽象为几何图形. 图中都有哪些角?你能说出图中的各个角之间都有怎样的关系吗?问题情境问题情境1. 在本图中,还有哪些角 互为余角?互为补角?互余的角有: ∠1与∠3,∠2与∠3,
∠1与∠4,∠2与∠4.互补的角有: ∠3与∠ABF,∠4与∠CBE,
∠3与∠CBE,∠4与∠ABF.探索发现2. 除了∠1=∠2外图中都有哪些相等的角?为什么?由此你能得到什么结论?同角的余角相等
等角的余角相等 ① ∠3=∠4
∵∠1= ∠2
∠ 1+∠3=90 0 ,
∠ 2+∠4=900
∴ ∠ 3=∠4探索发现同角的补角相等
等角的补角相等 ② ∠ABF=∠CBE
∵∠3= ∠4
∠ABF+∠3=180 0 ,∠CBE+∠4=1800
∴ ∠ABF=∠CBE探索发现(1)30 ,70 与80 的和为平角,所以这三个角互余( )
(2)一个角的余角必为锐角.( )
(3)一个角的补角必为钝角. ( )
(4)90 的角为余角.( )
(5)两角是否互补既与其大小有关又与其位置有关( )0×√××× 判断下列说法是否正确000课堂练习 如图,先找到长方形纸的宽DC的中点E,将∠C过点E折起任意一个角,折痕是EF,再将∠D过点E折起,使DE与HE重合,折痕是GE,请探索下列问题:
(1)∠GEF是直角吗?为什么?
(2)∠FEH与∠GEH互余吗?为什么?
(3) 在上述折纸的图形中,还有哪些角互为余角?还有哪些角互为补角?ADCBFEGH思维拓广余角、补角的概念:余角、补角的性质:(1) 和为直角的两个角称互为余角;
(2) 和为平角的两个角称互为补角;(1) 同角或等角的余角相等;
(2) 同角或等角的补角相等;
课堂小结课后作业
∠1与∠4,∠2与∠4.互补的角有: ∠3与∠ABF,∠4与∠CBE,
∠3与∠CBE,∠4与∠ABF.探索发现2. 除了∠1=∠2外图中都有哪些相等的角?为什么?由此你能得到什么结论?同角的余角相等
等角的余角相等 ① ∠3=∠4
∵∠1= ∠2
∠ 1+∠3=90 0 ,
∠ 2+∠4=900
∴ ∠ 3=∠4探索发现同角的补角相等
等角的补角相等 ② ∠ABF=∠CBE
∵∠3= ∠4
∠ABF+∠3=180 0 ,∠CBE+∠4=1800
∴ ∠ABF=∠CBE探索发现(1)30 ,70 与80 的和为平角,所以这三个角互余( )
(2)一个角的余角必为锐角.( )
(3)一个角的补角必为钝角. ( )
(4)90 的角为余角.( )
(5)两角是否互补既与其大小有关又与其位置有关( )0×√××× 判断下列说法是否正确000课堂练习 如图,先找到长方形纸的宽DC的中点E,将∠C过点E折起任意一个角,折痕是EF,再将∠D过点E折起,使DE与HE重合,折痕是GE,请探索下列问题:
(1)∠GEF是直角吗?为什么?
(2)∠FEH与∠GEH互余吗?为什么?
(3) 在上述折纸的图形中,还有哪些角互为余角?还有哪些角互为补角?ADCBFEGH思维拓广余角、补角的概念:余角、补角的性质:(1) 和为直角的两个角称互为余角;
(2) 和为平角的两个角称互为补角;(1) 同角或等角的余角相等;
(2) 同角或等角的补角相等;
课堂小结课后作业
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
