苏教版五年级下册数学《简易方程》复习课件(共17张PPT)
文档属性
| 名称 | 苏教版五年级下册数学《简易方程》复习课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 987.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 15:56:33 | ||
图片预览





文档简介
(共17张PPT)
苏教版 数学 五年级 下册
1.8整理与练习
1
简易方程
整体回顾
综合运用
课后作业
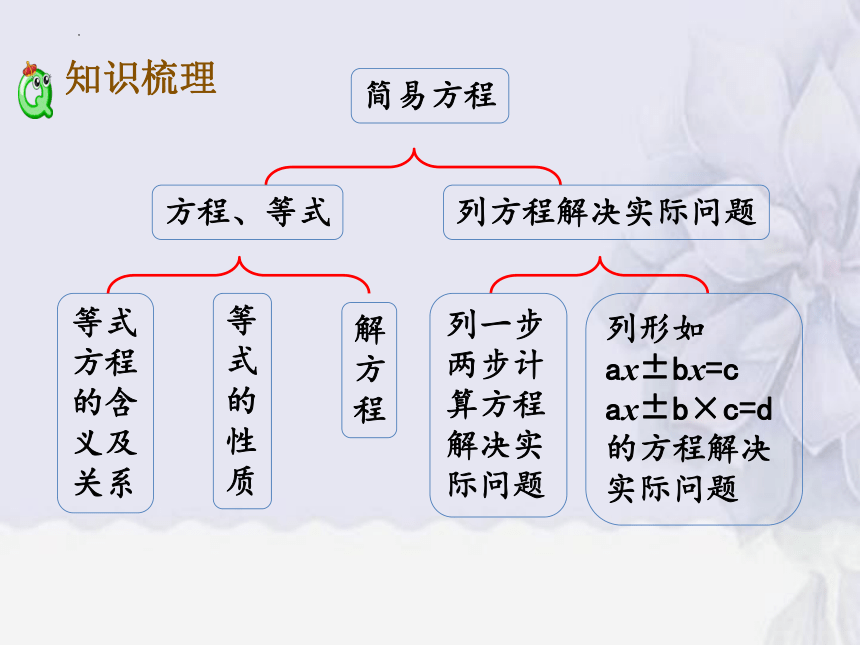
知识梳理
整体回顾
简易方程
方程、等式
列方程解决实际问题
等式方程的含义及关系
等式的性质
解方程
列一步两步计算方程解决实际问题
列形如
ax±bx=c
ax±b×c=d
的方程解决实际问题
知识梳理
含有未知数的等式是方程。
方程一定是等式,且必须含有未知数。
等式不一定是方程。
等式和方程的关系可表示如图:
使方程左右两边相等的未知数的值叫作方程的解,求方程的解的过程叫解方程。
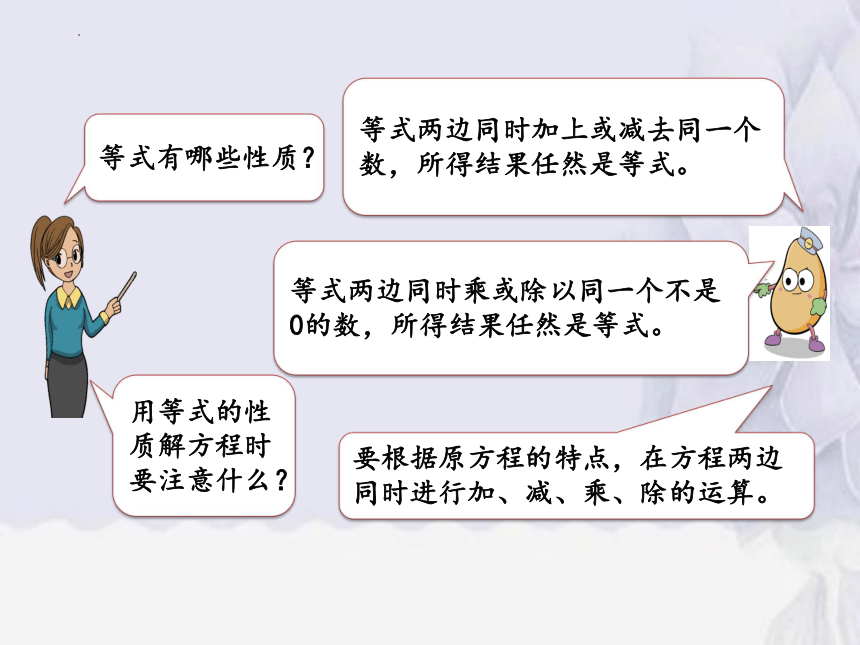
等式两边同时加上或减去同一个数,所得结果任然是等式。
等式两边同时乘或除以同一个不是0的数,所得结果任然是等式。
等式有哪些性质?
用等式的性质解方程时要注意什么?
要根据原方程的特点,在方程两边同时进行加、减、乘、除的运算。
一、自主复习
1.举例说一说等式和方程有什么联系和区别?
2.举例说一说方程、方程的解和解方程的含义。
3.等式有哪些性质?用等式的性质解方程时要注意什么?
4.在列方程解决实际问题时一般经过哪些步骤?怎样找到数量之间的相等关系?
二、合作探究
请大家围绕以上三个问题在小组中讨论交流。
1.举例说一说等式和方程有什么联系和区别?
2.举例说一说方程、方程的解和解方程的含义。
3.等式有哪些性质?用等式的性质解方程时要注意什么?
4.在列方程解决实际问题时一般经过哪些步骤?怎样找到数量之间的相等关系?
三、展示提升
1.判断下面的式子是不是等式?是不是方程?并说明理由。
①x + 2.4= 5
②15÷b
③3x + 4x = 28
④6n<3.6
⑤90 - a = 40
⑥4 y = 0.4
⑦4.9–3.7=1.2
⑧2a - 5b = 3
三、展示提升
2.解方程。
0.6 + x = 2.7
14x = 7
x -0.8 x = 10
四、小结强调
通过课的复习,你有什么收获?
1.等式的意义:表示相等关系的式子。
2.等式的性质
①等式两边同时加上或减去同一个数,所得结果仍然是等式。
②等式两边同时乘或除以同一个不等于0的数,所得结果仍然是等式。
3.方程的意义:含有未知数的等式叫作方程。
4.解方程
根据等式的性质来求方程的解,一般注意以下几点:
①不要忘记写“解"。
②等号上下对齐。
③解方程每一步写出的都应是一个含有未知数的等式,不可写成连等式或递等式。
④解方程后要检验(可以口头检验)。
四、小结强调
5.列方程解决实际问题步骤
①审题,弄懂题目的已知条件和所求问题。
②理清题目的等量关系。
③设未知数,一般把所求的量用x表示。
④根据等量关系列出方程。
⑤解方程。
⑥检验。
⑦写答语。
四、小结强调
6.列方程解决实际问题(和倍、差倍问题)
根据题目中给出的两个量相加或相减的数据,找出等量关系,列出形如ax±bx=c的方程,利用等式的性质求出方程的解并检验。
四、小结强调
五、检测反馈
1.解方程:
0.2χ=3.5 χ-1.2=7.2 2.1χ-χ=1.21
2.2x-0.5×2=10 3×1.5+2x=11.5 13x-7x=5.7
五、检测反馈
2.列方程解决实际问题
(1)学校印刷画册一共用去2240元,画册的印刷费是3.6元/本,其余费用是800元。学校印刷了多少本画册?
(2)猎豹追捕猎物时的速度大约是优秀短跑运动员百米赛跑速度的3倍,每秒大约比运动员多跑20米。优秀短跑运动员每秒大约跑多少米?猎豹呢?
六、拓展延伸
2.09÷χ=1.1
9.85-x=6.23
谢谢大家
苏教版 数学 五年级 下册
1.8整理与练习
1
简易方程
整体回顾
综合运用
课后作业
知识梳理
整体回顾
简易方程
方程、等式
列方程解决实际问题
等式方程的含义及关系
等式的性质
解方程
列一步两步计算方程解决实际问题
列形如
ax±bx=c
ax±b×c=d
的方程解决实际问题
知识梳理
含有未知数的等式是方程。
方程一定是等式,且必须含有未知数。
等式不一定是方程。
等式和方程的关系可表示如图:
使方程左右两边相等的未知数的值叫作方程的解,求方程的解的过程叫解方程。
等式两边同时加上或减去同一个数,所得结果任然是等式。
等式两边同时乘或除以同一个不是0的数,所得结果任然是等式。
等式有哪些性质?
用等式的性质解方程时要注意什么?
要根据原方程的特点,在方程两边同时进行加、减、乘、除的运算。
一、自主复习
1.举例说一说等式和方程有什么联系和区别?
2.举例说一说方程、方程的解和解方程的含义。
3.等式有哪些性质?用等式的性质解方程时要注意什么?
4.在列方程解决实际问题时一般经过哪些步骤?怎样找到数量之间的相等关系?
二、合作探究
请大家围绕以上三个问题在小组中讨论交流。
1.举例说一说等式和方程有什么联系和区别?
2.举例说一说方程、方程的解和解方程的含义。
3.等式有哪些性质?用等式的性质解方程时要注意什么?
4.在列方程解决实际问题时一般经过哪些步骤?怎样找到数量之间的相等关系?
三、展示提升
1.判断下面的式子是不是等式?是不是方程?并说明理由。
①x + 2.4= 5
②15÷b
③3x + 4x = 28
④6n<3.6
⑤90 - a = 40
⑥4 y = 0.4
⑦4.9–3.7=1.2
⑧2a - 5b = 3
三、展示提升
2.解方程。
0.6 + x = 2.7
14x = 7
x -0.8 x = 10
四、小结强调
通过课的复习,你有什么收获?
1.等式的意义:表示相等关系的式子。
2.等式的性质
①等式两边同时加上或减去同一个数,所得结果仍然是等式。
②等式两边同时乘或除以同一个不等于0的数,所得结果仍然是等式。
3.方程的意义:含有未知数的等式叫作方程。
4.解方程
根据等式的性质来求方程的解,一般注意以下几点:
①不要忘记写“解"。
②等号上下对齐。
③解方程每一步写出的都应是一个含有未知数的等式,不可写成连等式或递等式。
④解方程后要检验(可以口头检验)。
四、小结强调
5.列方程解决实际问题步骤
①审题,弄懂题目的已知条件和所求问题。
②理清题目的等量关系。
③设未知数,一般把所求的量用x表示。
④根据等量关系列出方程。
⑤解方程。
⑥检验。
⑦写答语。
四、小结强调
6.列方程解决实际问题(和倍、差倍问题)
根据题目中给出的两个量相加或相减的数据,找出等量关系,列出形如ax±bx=c的方程,利用等式的性质求出方程的解并检验。
四、小结强调
五、检测反馈
1.解方程:
0.2χ=3.5 χ-1.2=7.2 2.1χ-χ=1.21
2.2x-0.5×2=10 3×1.5+2x=11.5 13x-7x=5.7
五、检测反馈
2.列方程解决实际问题
(1)学校印刷画册一共用去2240元,画册的印刷费是3.6元/本,其余费用是800元。学校印刷了多少本画册?
(2)猎豹追捕猎物时的速度大约是优秀短跑运动员百米赛跑速度的3倍,每秒大约比运动员多跑20米。优秀短跑运动员每秒大约跑多少米?猎豹呢?
六、拓展延伸
2.09÷χ=1.1
9.85-x=6.23
谢谢大家
