变量与函数(河北省唐山市)

课件32张PPT。welcome 20.1变量与函数大千世界万物皆变行星在宇宙中的位置随时间而变化;人体细胞的个数随年龄而变化;气温随海拔而变化;汽车行驶里程随行驶时间而变化;……提出问题，创设情景 一辆汽车以60千米/小时的速度匀速行驶，行驶里程为S千米，行使时间为t小时.3.试用含t的式子表示S .2.在以上这个过程中，1.请同学们根据题意填写下表：60120180240300里程S千米与时间t时速度60千米/小时S=60t变化的量是 .没变化的量是 .t(t≥0)活动一 1. 每张电影票售价为10元，如果早场售出票150张，日场售出票205张，晚场售出310张. 三场电影的票房收入各多少元？设一场电影售票x张，票房收入y元。怎样用含x的式子表示 y ？(2) 关系式为：y=10x (1) 早场电影票收入：150×10=1500元 日场电影票收入：205×10=2050元 晚场电影票收入：310×10=3100元 2.在一根弹簧的下端悬挂重物，改变并记录重物的质量，观察并记录弹簧长度的变化，探索它们的变化规律。如果弹簧原长10cm，每1kg的重物使弹簧伸长0.5cm，怎样用含有重物质量m的的式子表示受力后弹簧的长度l？ 挂1kg重物时弹簧的长度：1×0.5+10=10.5（cm） 关系式为： l =0.5m+10 探究：结论：挂2kg重物时弹簧的长度：2×0.5+10=11（cm）挂3kg重物时弹簧的长度：3×0.5+10=11.5（cm） 3. 小明到商店买练习簿，每本单价2元，购买的总数 x（本）与总金额 y（元）的关系式，可以表示为:
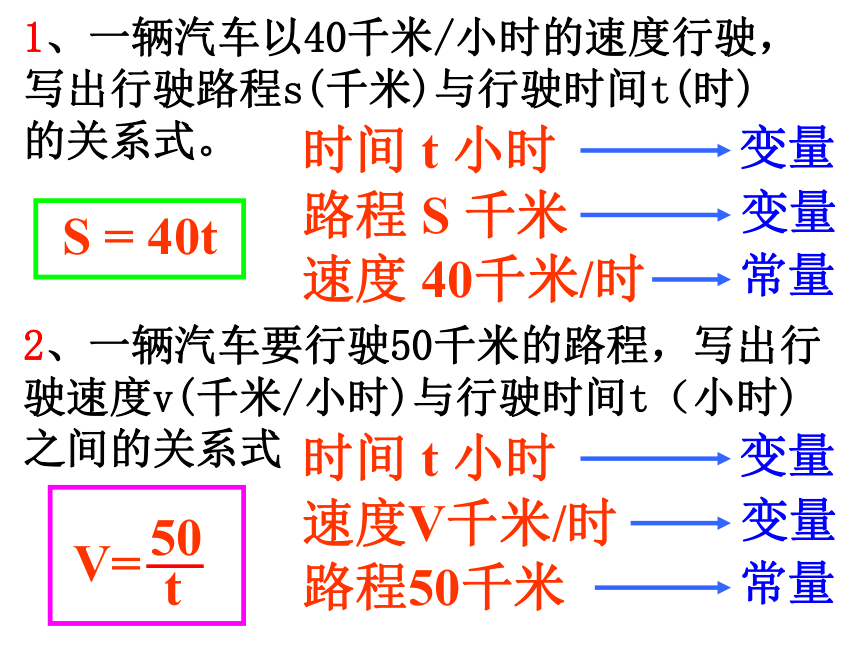
其中y随x的变化而变化y = 2x(x>0的整数）定义： 在上述活动中，我们要想寻求事物变化过程的规律，首先需要确定在这个过程中哪些量是变化的，而哪些量又是不变的。 在一个变化过程中，可以取不同数值的量叫做变量 售出票数x、票房收入y；重物质量m、弹簧长度l都是变量.而票价10元，弹簧原长10cm……都是常量.例如：而数值保持不变的量称之为常量.1、一辆汽车以40千米/小时的速度行驶，
写出行驶路程s(千米)与行驶时间t(时)
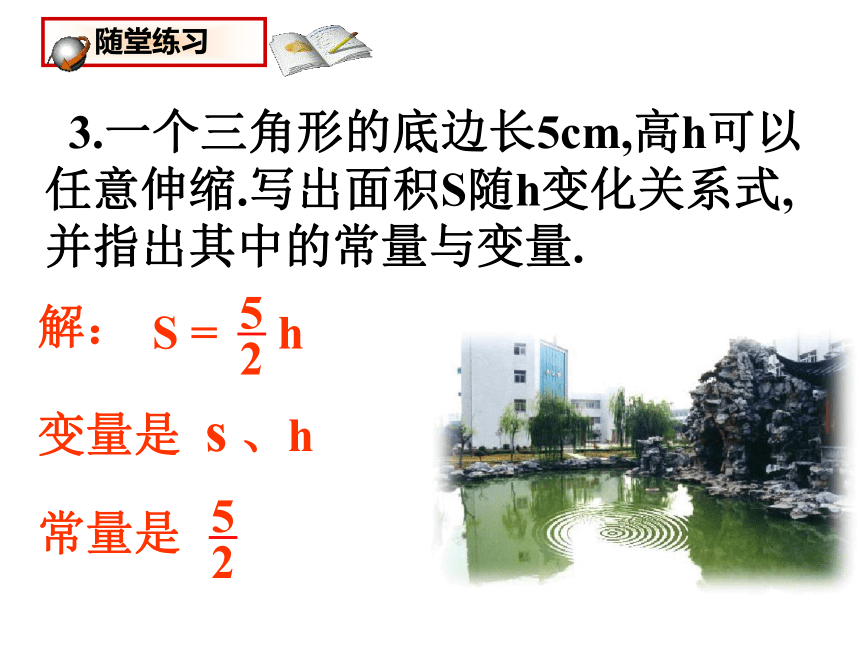
的关系式。 2、一辆汽车要行驶50千米的路程，写出行驶速度v(千米/小时)与行驶时间t（小时)之间的关系式 S = 40t时间 t 小时速度 40千米/时路程 S 千米 变量变量常量时间 t 小时路程50千米速度V千米/时 变量变量常量随堂练习：VRQ=40-5t其中变量是 、 ，常量是 . Q、t40、5 3.一个三角形的底边长5cm,高h可以任意伸缩.写出面积S随h变化关系式,并指出其中的常量与变量.解：变量是 s 、h 4.夏季高山上温度从山脚起每升高100米降低 0.7℃，已知山脚下温度是23℃，写出温度y与上升高度 x之间的关系式，并指出其中的常量与变量。解：y =23 -0.007x变量是 x 、y常量是 23、0.007请你举出生活中变化的实例，
并指出其中的常量与变量。
完成下列问题，并指出其中的变量与常量。1、圆的周长C与半径r的函数关系式：________________常 量：变 量：c, r2、n边形的内角和S与边数n的函数关系式：____________________s=(n-2) ×1800常 量：变 量：n, s2, 1803、等腰三角形的顶角为x度，那么底角y的度数用含x的式子表示为______________.常 量：变 量：x,y2, 180复习回顾 一辆汽车以60千米/小时的速度匀速行驶，行驶里程S千米与行使时间t小时的关系是：S=60t（1）问题中有几个变量？两个变量 t 、S（2）这两个变量有什么关系？拓展题 瓶子或罐头盒等物体常如下图那样堆放，试确定瓶子总数y与层数x之间的关系式.拓展题 瓶子或罐头盒等物体常如下图那样堆放，试确定瓶子总数y与层数x之间的关系式.11+21+2+31+2+3+ …+x瓶子总数y 与层数x之间的关系式：x 当时间 t 取定一个值时，行驶里程S就随之确定一个值。 关系式为： l =0.5m+10 m千克l厘米 当重物质量 m 取定一个值时，受力后弹簧的长度 l 就随之确定一个值。定义 在一个变化过程中，如果有两个变量 x、y，对于x的每个确定的值，y都有唯一确定的值与其对应，那么我们就说y是x的函数,x叫做自变量.（1）在 S= 60t 中，S是t 的函数，（2）在 l =0.5m+10中， t 是自变量； l 是 m 的函数， m 是自变量；1、某日的气温变化图
从图中我们可以看到，随着时间t（时）
的变化，相应地气温T（℃）也随之变化． 观 察: 对于时间t的每一个确定的值，温度T都有唯一确定的对应值吗？T是t的函数.2、 2002年7月中国工商银行为
“整存整取”的存款方式规定的利率
观察上表，说说随着存期x的增长，
相应的利率y是如何变化的．观 察: （1）通过前面的例子，大家想一想：我们可以用哪些方法表示一些函数？写式子、图象、表格这三种表示函数的方法分别称为：解析式法，图象法，列表法。 （2）结合前面的例子，你认为三种表示函数的方法各有什么优点？议一议 解析式法可以从数量关系的角度明确自变量与函数的对应关系； 图象法可以直观形象地反映函数的变化趋势，而且对于无法用解析式表达的函数，图象可以充当重要角色； 列表法可以清楚地列出一些自变量与函数的对应值这会对某些特定的数值带来一目了然的效果，例如火车时刻表……例 下列问题中的变量y是不是x的函数？是（1）在 y = 2x 中的y与x；是不是（4）在 中的y与x；是（5）在 中的y与x；不是活动二 1. 要画一个面积为10 圆，圆的半径应取多少？圆的面积为20 呢？怎样用含有圆面积S的式子表示圆半径r？ 探究： 圆面积公式 面积为10 的圆半径 面积为20 的圆半径 函数解析式为： 因为所以2.用10cm长的绳子围成矩形，试改变矩形的长、宽，观察矩形的面积怎样变化，试举出三组长、宽的值。计算相应矩形的面积的值，然后探索它们的变化规律：设矩形的长度为xcm，面积为S ，怎样用含x的式子表示S？12.用10cm长的绳子围成矩形，试改变矩形的长、宽，观察矩形的面积怎样变化，试举出三组长、宽的值。计算相应矩形的面积的值，然后探索它们的变化规律：设矩形的长度为xcm，面积为S ，怎样用含x的式子表示S？长 x 米宽 (5-x) 米432.5122.5面积 s 米2466.25解：3、正方形的边长为5 cm,当边长减少x cm时，周长为y cm，求y与x的函数关系式。作业课后思考题与练习题数学日记作业：作业本（1）再见