初中数学人教版八上同步课件 12.2第1课时三角形全等的判定(一)(共30张PPT)
文档属性
| 名称 | 初中数学人教版八上同步课件 12.2第1课时三角形全等的判定(一)(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 21:06:01 | ||
图片预览










文档简介
(共30张PPT)
第十二章 全等三角形
12.2 三角形全等的判定
第1课时 三角形的全等的判定(一)(SSS)
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
2.理解并掌握“边边边”判定方法,能利用“边边边”证明两个三角形全等.(重点)
3.会用尺规作一个角等于已知角,了解图形的作法.(难点)
新课导入
复习引入
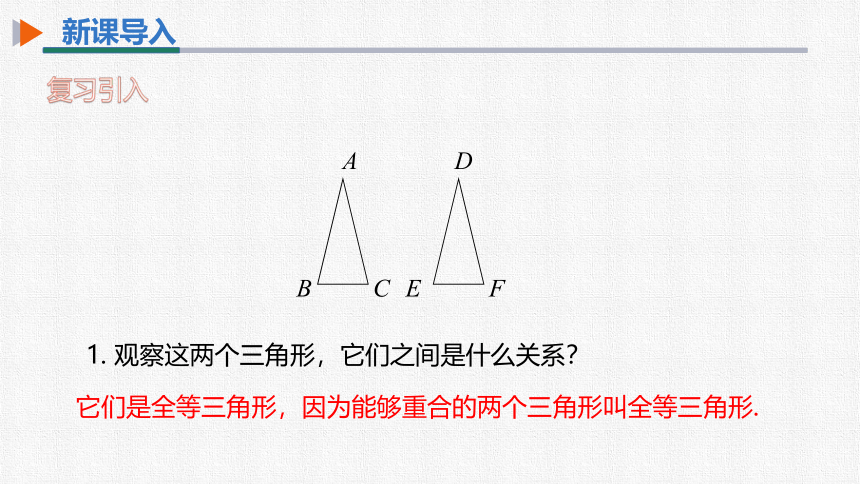
1. 观察这两个三角形,它们之间是什么关系?
它们是全等三角形,因为能够重合的两个三角形叫全等三角形.
A
B
C
D
E
F
新课导入
复习引入
2.如图,已知△ABC与△DEF全等,用几何语言表达全等三角形的性质, 找出其中相等的边与角.
∵△ABC≌△DEF,
∴AB=DE,AC=DF,BC=EF;(全等三角形对应边相等)
∠A=∠D,∠B=∠E,∠C=∠F.(全等三角形对应角相等)
A
B
C
D
E
F
新课导入
复习引入
想一想:
如果AB=DE,AC=DF,BC=EF;∠A=∠D,∠B=∠E,∠C=∠F,那么△ABC 和△△DEF能够完全重合,即可判定△ABC≌△△DEF.
一定要满足三条边分别相等,三个角分别相等,才能保证两个三角形全等吗?能否选取其中的一部分条件,简捷地判定两个三角形全等呢?
新知探究
知识点1 探究判定三角形全等的条件
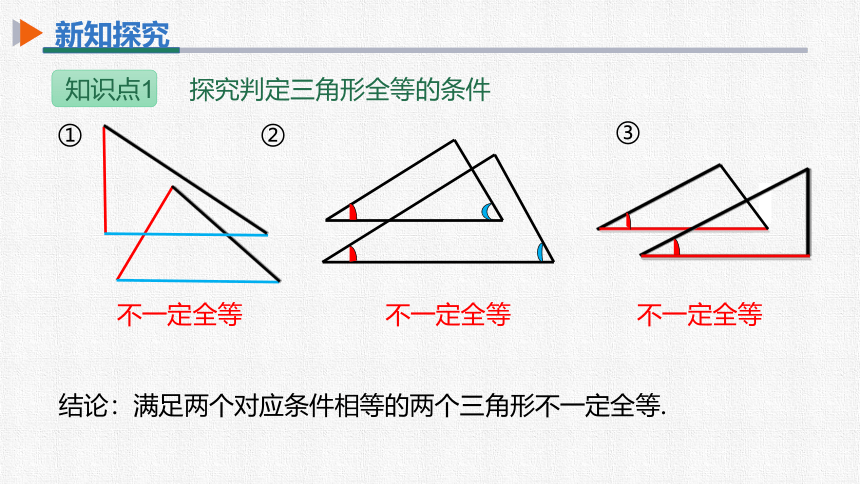
探究1 (1)一个对应条件可以吗?
画出两个三角形,使得满足一个相等条件,此时的两三角形全等吗?
①只有一条边相等(假设为3cm).
不一定全等
新知探究
②只有一个角相等(假设为45°).
结论:满足一个对应条件相等的两个三角形不一定全等.
不一定全等
知识点1 探究判定三角形全等的条件
新知探究
探究1 (2)两个对应条件可以吗?
知识点1 探究判定三角形全等的条件
有几种情况?
新知探究
①有两条边对应相等(假设一条边为3cm,另一条边为4cm).
知识点1 探究判定三角形全等的条件
画出两个三角形,使得满足两个相等条件,此时的两三角形全等吗?
②有两个角对应相等(假设一个角为30°,另一个角为60°).
③有一条边和一个角分别对应相等(假设一条边为4cm,一个角为30°).
新知探究
①
不一定全等
知识点1 探究判定三角形全等的条件
不一定全等
②
③
不一定全等
结论:满足两个对应条件相等的两个三角形不一定全等.
新知探究
知识点1 探究判定三角形全等的条件
由探究1可知,满足六个条件中的一个或两个条件对应相等,都不能保证两个三角形全等,那么满足六个条件中的三个条件对应相等,能否保证两个三角形全等呢?
新知探究
知识点2 “SSS”证全等
探究2 先任意画出一个△ABC,再画出一个△A'B'C',使得A'B'=AB,B'C'=BC,C'A'=CA,把画好的△A'B'C'剪下来,放到△ABC上,它们全等吗?
动手试一试
新知探究
知识点2 “SSS”证全等
画一个△A'B'C',使得A'B'=AB,B'C'=BC,C'A'=CA.
A
B
C
A ′
B′
C′
画法:
(1)画线段B'C'=BC;
(2)分别以B',C'为圆心,线段 AB, AC 为半径画弧,两弧相交于点A';
(3)连接线段A'B',A'C'.
新知探究
知识点2 “SSS”证全等
想一想:探究2的结果反映了什么规律?你能用文字语言和符号语言概括吗?
三边分别相等的两个三角形全等(可以简写为“边边边”或“SSS”).
该基本事实可以用来判定两个三角形全等
新知探究
知识点2 “SSS”证全等
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
AB=A'B',
BC=B'C',
CA=C'A',
该判定定理的几何语言:
就是说,三角形三条边的长度确定了,这个三角形的形状、大小也就确定了,这也是三角形具有稳定性的原因.
新知探究
知识点2 “SSS”证全等
例1 在如图所示的三角形钢架中,AB =AC ,AD 是连接点A与BC 中点D的支架.求证:△ABD≌△ACD .
C
B
D
A
【分析】要证△ABD≌△ACD,只要看这两个三角形的三条边是否分别相等.先找现有条件(AB=AC),再找隐含条件(公共边AD),最后找准备条件(D是BC的中点,可知BD=CD).
例 在如图所示的三角形钢架中,AB =AC ,AD是连接点A与BC 中点D的支架.求证:△ABD≌△ACD .
新知探究
知识点2 “SSS”证全等
C
B
D
A
证明:∵D 是BC中点,∴BD =DC.
在△ABD与△ACD 中,
∴△ABD ≌ △ACD(SSS).
AB =AC,
BD =CD,
AD =AD,
新知探究
知识点2 “SSS”证全等
证明:∵D 是BC中点,
∴BD =DC.
在△ABD与△ACD 中,
∴△ABD ≌ △ACD( SSS ).
AB =AC ,
BD =CD ,
AD =AD ,
证明三角形全等的书写步骤与规则
①准备条件:证全等时要用的条件要先证好(在已知中找,在图形中看);
②指明范围:写出在哪两个三角形中证全等;
③摆齐根据:按基本事实的顺序列出三个条件(一般是把同一个三角形的三个条件放在等号的同一侧),并用大括号括起来;
④写出结论:写出全等结论.
跟踪训练
新知探究
(2021 云南)如图,在四边形ABCD中,AD=BC,AC=BD,AC与BD相交于点E.求证:∠DAC=∠CBD.
在图形中,通过证明两个三角形全等,可以为进一步寻求边等、角等、线段间的特殊关系等提供了方法和依据.
证明:在△CDA和△DCB中,
AD=BC,
AC=BD,
DC=CD,
∴△CDA≌△DCB(SSS),
∴∠DAC=∠CBD.
有些题目的已知条件隐含在题设或图形之中,如公共边,公共角,对顶角等.
新知探究
知识点3 用尺规作一个角等于已知角
已知:∠AOB.
求作: ∠A'O'B'=∠AOB.
由三边分别相等判定三角形全等的结论,还可以得到用直尺和圆规作一个角等于已知角的方法.
O
B
A
新知探究
知识点3 用尺规作一个角等于已知角
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,OB 于点C,D;
O
D
B
C
A
O′
C′
A′
(2)画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';
新知探究
知识点3 用尺规作一个角等于已知角
(3)以点C'为圆心,CD 长为半径画弧,与第2步中所画的弧交于点D';
O
D
B
C
A
O′
C′
A′
B′
D ′
(4)过点D'画射线O'B',则∠AOB=∠A'O'B'.
想一想,为什么这样作出的∠A'O'B'和∠AOB是相等的?
课堂小结
三角形的全等的判定(一)(SSS)
三角形的全等的判定分类探究
边边边(SSS)
证明三角形全等的书写步骤与规则
只满足一个条件或者两个条件对应相等时不能判定三角形全等
三边分别相等的两个三角形全等
作一个角等于已知角
课堂训练
1.如图,在△ABC中,BC=AC,BE=AE,则由“SSS”可以判定( )A.△ACD≌△BCD B.△ADE≌△BDE
C.△ACE≌△BCE D.以上都对
C
课堂训练
2.如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使能利用“SSS”判定△ABC≌△EDF,需添加的条件为 .
BC=DF
【解析】利用SSS判定,则两三角形的三条边应对应相等. 添加BC=DF.
∵AD=BE,∴AD+DB=BE+BD,即AB=ED.
又知AC=EF,∴添加的条件是BC=DF时,可证得△ABC≌△EDF.
等边加同边,其和还是等边.
课堂训练
3.(2021 东莞市二模)如图,OA=OB,AC=BC,∠ACO=30°,则∠ACB= .
60°
【解析】在△ACO和△BCO中, OA=OB,
AC=BC,
OC=OC,
∴△AOC≌△BOC(SSS).∴∠BCO=∠ACO=30°.
∴∠ACB=∠BCO+∠ACO=60°,故答案为60°.
课堂训练
4.如图,AB=AC,DB=DC,请说明∠B=∠C.
解: 连接AD.
在△ABD和△ACD中,
AB=AC,
DB=DC,
AD=AD,
∴ △ABD≌△ACD(SSS).
∴∠B=∠C.
A
B
D
C
学会作辅助线帮助解题.
课堂训练
5.如图,在△ABC中,AB=AC,D,E是BC的三等分点,AD=AE,求证:△ABE≌△ACD.
证明:∵D,E是BC的三等分点,
∴BD+DE=DE+EC,即BE=CD .
∴BD=DE=EC .
在△ABE和△ACD中,
AE=AD,
AB=AC,
BE=CD,
∴△ABE≌△ACD(SSS).
等边加同边,其和还是等边.
课堂训练
6.如图,已知AC=FE,AD=FB,BC=DE.求证:AC//EF,DE//BC.
证明:∵AD=FB,∴AD+DB=FB+BD,即AB=FD.
在△ABC和△FDE中,
AC=FE,
BC=DE,
AB=FD,
∴△ABC≌△FDE(SSS),∴∠A=∠F,∠ABC=∠FDE.
∴AC//EF,DE//BC.
A
C
B
D
E
F
等边加同边,其和还是等边.
课堂训练
7.如图,过点C作直线DE,使DE//AB.
(2)在直线MN的右侧作∠FCE,使∠FCE=∠AFC;
解:作法:
(1)过点C作直线MN与AB相交,交点为F;
(3)反向延长CE,则直线DE即为所求.
A
B
C
M
N
E
D
F
第十二章 全等三角形
12.2 三角形全等的判定
第1课时 三角形的全等的判定(一)(SSS)
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
2.理解并掌握“边边边”判定方法,能利用“边边边”证明两个三角形全等.(重点)
3.会用尺规作一个角等于已知角,了解图形的作法.(难点)
新课导入
复习引入
1. 观察这两个三角形,它们之间是什么关系?
它们是全等三角形,因为能够重合的两个三角形叫全等三角形.
A
B
C
D
E
F
新课导入
复习引入
2.如图,已知△ABC与△DEF全等,用几何语言表达全等三角形的性质, 找出其中相等的边与角.
∵△ABC≌△DEF,
∴AB=DE,AC=DF,BC=EF;(全等三角形对应边相等)
∠A=∠D,∠B=∠E,∠C=∠F.(全等三角形对应角相等)
A
B
C
D
E
F
新课导入
复习引入
想一想:
如果AB=DE,AC=DF,BC=EF;∠A=∠D,∠B=∠E,∠C=∠F,那么△ABC 和△△DEF能够完全重合,即可判定△ABC≌△△DEF.
一定要满足三条边分别相等,三个角分别相等,才能保证两个三角形全等吗?能否选取其中的一部分条件,简捷地判定两个三角形全等呢?
新知探究
知识点1 探究判定三角形全等的条件
探究1 (1)一个对应条件可以吗?
画出两个三角形,使得满足一个相等条件,此时的两三角形全等吗?
①只有一条边相等(假设为3cm).
不一定全等
新知探究
②只有一个角相等(假设为45°).
结论:满足一个对应条件相等的两个三角形不一定全等.
不一定全等
知识点1 探究判定三角形全等的条件
新知探究
探究1 (2)两个对应条件可以吗?
知识点1 探究判定三角形全等的条件
有几种情况?
新知探究
①有两条边对应相等(假设一条边为3cm,另一条边为4cm).
知识点1 探究判定三角形全等的条件
画出两个三角形,使得满足两个相等条件,此时的两三角形全等吗?
②有两个角对应相等(假设一个角为30°,另一个角为60°).
③有一条边和一个角分别对应相等(假设一条边为4cm,一个角为30°).
新知探究
①
不一定全等
知识点1 探究判定三角形全等的条件
不一定全等
②
③
不一定全等
结论:满足两个对应条件相等的两个三角形不一定全等.
新知探究
知识点1 探究判定三角形全等的条件
由探究1可知,满足六个条件中的一个或两个条件对应相等,都不能保证两个三角形全等,那么满足六个条件中的三个条件对应相等,能否保证两个三角形全等呢?
新知探究
知识点2 “SSS”证全等
探究2 先任意画出一个△ABC,再画出一个△A'B'C',使得A'B'=AB,B'C'=BC,C'A'=CA,把画好的△A'B'C'剪下来,放到△ABC上,它们全等吗?
动手试一试
新知探究
知识点2 “SSS”证全等
画一个△A'B'C',使得A'B'=AB,B'C'=BC,C'A'=CA.
A
B
C
A ′
B′
C′
画法:
(1)画线段B'C'=BC;
(2)分别以B',C'为圆心,线段 AB, AC 为半径画弧,两弧相交于点A';
(3)连接线段A'B',A'C'.
新知探究
知识点2 “SSS”证全等
想一想:探究2的结果反映了什么规律?你能用文字语言和符号语言概括吗?
三边分别相等的两个三角形全等(可以简写为“边边边”或“SSS”).
该基本事实可以用来判定两个三角形全等
新知探究
知识点2 “SSS”证全等
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
AB=A'B',
BC=B'C',
CA=C'A',
该判定定理的几何语言:
就是说,三角形三条边的长度确定了,这个三角形的形状、大小也就确定了,这也是三角形具有稳定性的原因.
新知探究
知识点2 “SSS”证全等
例1 在如图所示的三角形钢架中,AB =AC ,AD 是连接点A与BC 中点D的支架.求证:△ABD≌△ACD .
C
B
D
A
【分析】要证△ABD≌△ACD,只要看这两个三角形的三条边是否分别相等.先找现有条件(AB=AC),再找隐含条件(公共边AD),最后找准备条件(D是BC的中点,可知BD=CD).
例 在如图所示的三角形钢架中,AB =AC ,AD是连接点A与BC 中点D的支架.求证:△ABD≌△ACD .
新知探究
知识点2 “SSS”证全等
C
B
D
A
证明:∵D 是BC中点,∴BD =DC.
在△ABD与△ACD 中,
∴△ABD ≌ △ACD(SSS).
AB =AC,
BD =CD,
AD =AD,
新知探究
知识点2 “SSS”证全等
证明:∵D 是BC中点,
∴BD =DC.
在△ABD与△ACD 中,
∴△ABD ≌ △ACD( SSS ).
AB =AC ,
BD =CD ,
AD =AD ,
证明三角形全等的书写步骤与规则
①准备条件:证全等时要用的条件要先证好(在已知中找,在图形中看);
②指明范围:写出在哪两个三角形中证全等;
③摆齐根据:按基本事实的顺序列出三个条件(一般是把同一个三角形的三个条件放在等号的同一侧),并用大括号括起来;
④写出结论:写出全等结论.
跟踪训练
新知探究
(2021 云南)如图,在四边形ABCD中,AD=BC,AC=BD,AC与BD相交于点E.求证:∠DAC=∠CBD.
在图形中,通过证明两个三角形全等,可以为进一步寻求边等、角等、线段间的特殊关系等提供了方法和依据.
证明:在△CDA和△DCB中,
AD=BC,
AC=BD,
DC=CD,
∴△CDA≌△DCB(SSS),
∴∠DAC=∠CBD.
有些题目的已知条件隐含在题设或图形之中,如公共边,公共角,对顶角等.
新知探究
知识点3 用尺规作一个角等于已知角
已知:∠AOB.
求作: ∠A'O'B'=∠AOB.
由三边分别相等判定三角形全等的结论,还可以得到用直尺和圆规作一个角等于已知角的方法.
O
B
A
新知探究
知识点3 用尺规作一个角等于已知角
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,OB 于点C,D;
O
D
B
C
A
O′
C′
A′
(2)画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';
新知探究
知识点3 用尺规作一个角等于已知角
(3)以点C'为圆心,CD 长为半径画弧,与第2步中所画的弧交于点D';
O
D
B
C
A
O′
C′
A′
B′
D ′
(4)过点D'画射线O'B',则∠AOB=∠A'O'B'.
想一想,为什么这样作出的∠A'O'B'和∠AOB是相等的?
课堂小结
三角形的全等的判定(一)(SSS)
三角形的全等的判定分类探究
边边边(SSS)
证明三角形全等的书写步骤与规则
只满足一个条件或者两个条件对应相等时不能判定三角形全等
三边分别相等的两个三角形全等
作一个角等于已知角
课堂训练
1.如图,在△ABC中,BC=AC,BE=AE,则由“SSS”可以判定( )A.△ACD≌△BCD B.△ADE≌△BDE
C.△ACE≌△BCE D.以上都对
C
课堂训练
2.如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使能利用“SSS”判定△ABC≌△EDF,需添加的条件为 .
BC=DF
【解析】利用SSS判定,则两三角形的三条边应对应相等. 添加BC=DF.
∵AD=BE,∴AD+DB=BE+BD,即AB=ED.
又知AC=EF,∴添加的条件是BC=DF时,可证得△ABC≌△EDF.
等边加同边,其和还是等边.
课堂训练
3.(2021 东莞市二模)如图,OA=OB,AC=BC,∠ACO=30°,则∠ACB= .
60°
【解析】在△ACO和△BCO中, OA=OB,
AC=BC,
OC=OC,
∴△AOC≌△BOC(SSS).∴∠BCO=∠ACO=30°.
∴∠ACB=∠BCO+∠ACO=60°,故答案为60°.
课堂训练
4.如图,AB=AC,DB=DC,请说明∠B=∠C.
解: 连接AD.
在△ABD和△ACD中,
AB=AC,
DB=DC,
AD=AD,
∴ △ABD≌△ACD(SSS).
∴∠B=∠C.
A
B
D
C
学会作辅助线帮助解题.
课堂训练
5.如图,在△ABC中,AB=AC,D,E是BC的三等分点,AD=AE,求证:△ABE≌△ACD.
证明:∵D,E是BC的三等分点,
∴BD+DE=DE+EC,即BE=CD .
∴BD=DE=EC .
在△ABE和△ACD中,
AE=AD,
AB=AC,
BE=CD,
∴△ABE≌△ACD(SSS).
等边加同边,其和还是等边.
课堂训练
6.如图,已知AC=FE,AD=FB,BC=DE.求证:AC//EF,DE//BC.
证明:∵AD=FB,∴AD+DB=FB+BD,即AB=FD.
在△ABC和△FDE中,
AC=FE,
BC=DE,
AB=FD,
∴△ABC≌△FDE(SSS),∴∠A=∠F,∠ABC=∠FDE.
∴AC//EF,DE//BC.
A
C
B
D
E
F
等边加同边,其和还是等边.
课堂训练
7.如图,过点C作直线DE,使DE//AB.
(2)在直线MN的右侧作∠FCE,使∠FCE=∠AFC;
解:作法:
(1)过点C作直线MN与AB相交,交点为F;
(3)反向延长CE,则直线DE即为所求.
A
B
C
M
N
E
D
F
