数学七年级下青岛版8角复习课件

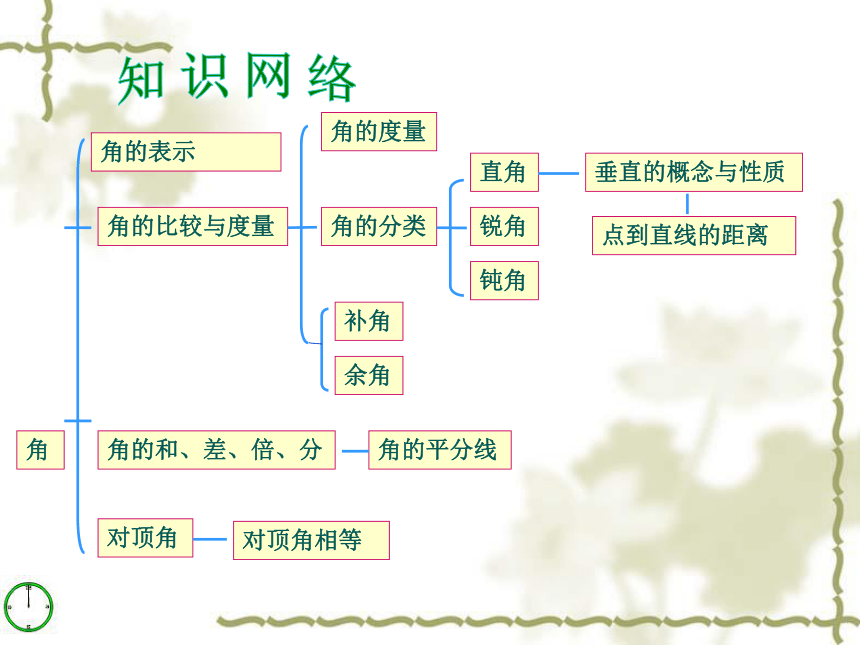
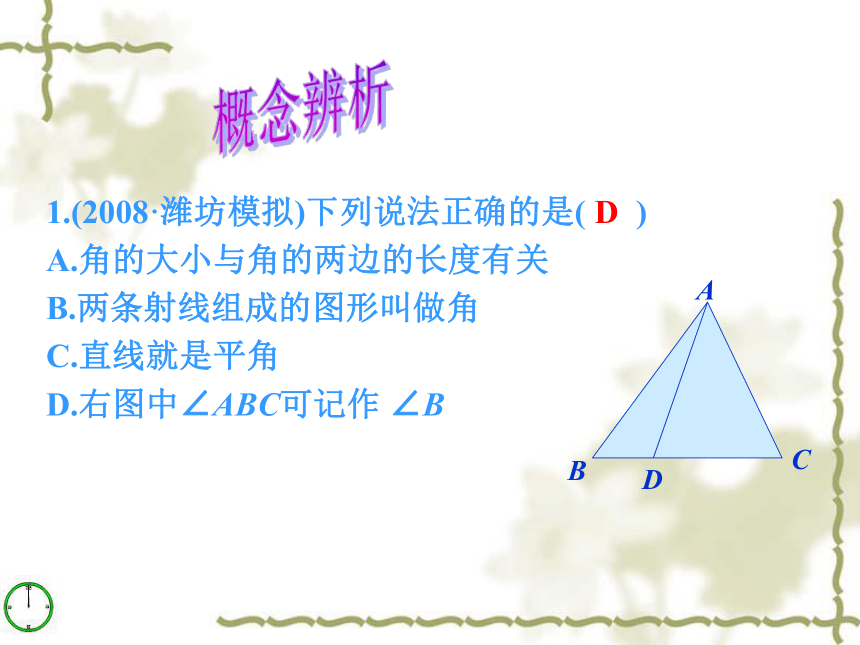
课件18张PPT。复习课第八章：角知识网络角角的度量1.(2008·潍坊模拟)下列说法正确的是( )
A.角的大小与角的两边的长度有关
B.两条射线组成的图形叫做角
C.直线就是平角
D.右图中∠ABC可记作 ∠BD概念辨析2.判断正误
(1)直线是平角,射线是周角;( )
(2)点P不在∠A的内部,就在∠A的外部;( )
(3)大于直角的角是钝角,小于直角的角是锐角.( )
(4)同一个角的两个邻补角是对顶角( )×××√例1. 点O在直线AB上,OC为射线, ∠1比∠2的3倍少10°,求∠1与∠2的度数专题一 方程的思想解:设∠2=x°, 则∠1=(3x－10)°
∵ ∠1＋ ∠2=180°
∴(3x －10) ＋x=180
解得 x=47.5
∴ ∠1=(3x－10)°=(3×47.5－10) °
=132.5°
∴ ∠1 =132.5°, ∠2=47.5°例2. 一个角的补角比它的余角的2倍多10°,求这个角解:设这个角为a ,根据题意得
(180°－a) －2(90°－ a)=10°
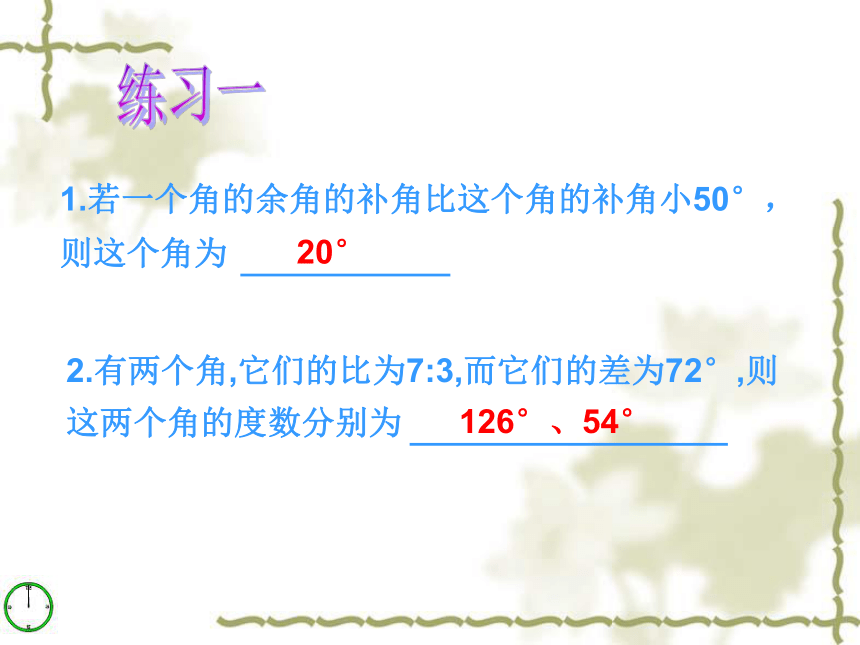
解得 a=10°1.若一个角的余角的补角比这个角的补角小50°，则这个角为 练习一2.有两个角,它们的比为7:3,而它们的差为72°,则这两个角的度数分别为20°126°、54°练习一3.如图,AB是街道,点O表 示一家超市,点C、D是两个居民小区,设计人员不小心把∠1、 ∠2、 ∠3的度数弄丢了,身边没有量角器,只知道∠1－ ∠2= ∠2 －∠3,则∠2 的度数是60°专题二 数形结合的思想解：∵ EO⊥AB，
∴ ∠AOE=90°
∴ ∠2= 90°－ ∠1= 90°－ 27°20′ = 62°40′
∵ ∠AOD=180°－ ∠1=180°－ 27°20′ = 152°40′
又∵ ∠3=∠FOD,
∴ ∠3= 0.5 ∠AOD = 152°40′×0.5 =76°20′
∴ ∠2 = 62°40′, ∠3= 76°20′例3. 已知，AB和CD都是直线,EO⊥AB, ∠3=∠FOD, ∠1=27°20′,求∠2、 ∠3.如图，直线AB，CD相交于点O，OE平分∠AOD，∠FOC=87°，∠1=40°，求∠2与∠3的度数.练习二解: ∵ ∠AOD=∠FOC＋ ∠1
= 87 ° ＋40 °=127°
又∵ OE平分∠AOD
∴ ∠2=0.5 ∠AOD
=0.5 × 127°=63.5°
∵ ∠3＋ ∠AOD=180 °
∴ ∠3= 180 °－∠AOD
= 180 °－ 127°=53 °例4 .已知线段AB的长为10cm,点A、B点直线l的距离分别为6cm和4cm，则符合条件的直线条数为（ ）
A.1条 B.2条 C.3条 D.4条专题三 分类讨论的思想C已知∠AOB=40°,以O为顶点,OB为边作∠BOC=10°,求∠AOC的度数或解:当∠BOC在∠AOB外部时,
∠AOC= ∠AOB＋∠BOC= 40°＋10°=50°;
当∠BOC在∠AOB内部时,
∠AOC= ∠AOB－ ∠BOC= 40°－ 10°=30°练习三例5. 如图,点D、E在BC上, ∠BDF和∠AEG都是直角,且∠1= ∠2,那么∠3= ∠4吗?说明理由.专题四 推理的方法解: ∠3= ∠4.理由如下:
∵ ∠1+ ∠3+ ∠BDF=180°
∠2+ ∠4+ ∠AEG=180°
又∵ ∠BDF=∠AEG=90°
∴ ∠1+ ∠3 = ∠2+ ∠4 =90°
∵ ∠1= ∠2
∴ ∠3= ∠4取一张长方形纸片,按下列方法折纸,然后回答问题
(1) ∠1与∠AEC, ∠3与∠BED分别有怎样的关系?
(2)AE与DE垂直吗?为什么?
(3) ∠1与∠3有怎样的关系?说明理由挑战自我ABECD1.（2008·乐山）直线l1与 l2相交于点O，OM⊥ l1， 若∠1=44°，则∠2=（ ）
A.56° B.46° C. 45° D.44°
中考链接B2.(2008·淮安)直线AB、CD相交于O，OE平分∠AOD，若∠BOD=100°，则∠AOE的度数是（ ）
A.40° B.50° C.80° D.100°中考链接A3.(2008·西宁中考)如图,将一副三角板叠放在一起,使直角的顶点重合于点O，则∠AOC＋ ∠DOB=( )中考链接180°说说你的收获