初中数学人教版八上同步课件:12.2三角形全等的判定(三)(第3课时)(35张PPT)
文档属性
| 名称 | 初中数学人教版八上同步课件:12.2三角形全等的判定(三)(第3课时)(35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 21:53:17 | ||
图片预览






文档简介
(共35张PPT)
第十二章 全等三角形
12.2 三角形全等的判定
第3课时 三角形的全等的判定(三)(ASA,AAS)
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.探索并正确理解三角形全等的判定方法“ASA”和“AAS”.
(重点)
2.能熟练利用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.(难点)
新课导入
复习引入
1.回顾我们已经学习过的判定三角形全等的两个定理.
边边边(SSS):三边分别相等的两个三角形全等.
边角边(SAS):两边和它们的夹角分别相等的两个三角形全等.
新课导入
复习引入
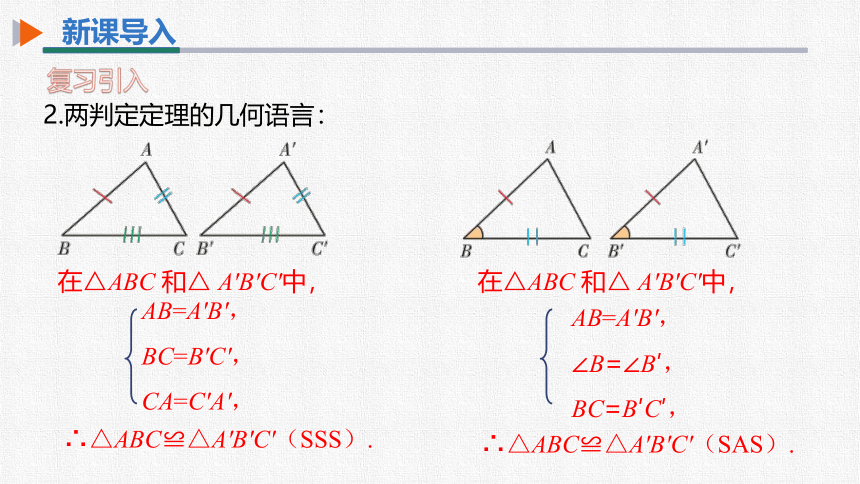
2.两判定定理的几何语言:
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
AB=A'B',
BC=B'C',
CA=C'A',
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(SAS).
AB=A'B',
∠B=∠B′,
BC=B′C′,
新课导入
复习引入
3.(1)我们已经总结过的找相等边的方法.
③等边加同边,其和还是等边.
①公共边.
(2)我们已经总结过的找相等角的方法.
①利用平行线可找到相等的角.
②正多边形的边相等.
②对顶角.
③等角加同角,其和还是等角.
④等角减同角,其差还是等角.
⑤等角的补角相等.
⑥正多边形的内角相等.
④等边减同边,其差还是等边.
新课导入
复习引入
4.当两个三角形满足六个条件中的“三个对应条件相等”时,有以下四种情况:
三个角对应相等
三条边对应相等
两条边和一个角对应相等 SAS
SSA
两个角和一条边对应相等
全等
不一定全等
不一定全等
全等
?
新知探究
知识点1 “ASA”证全等
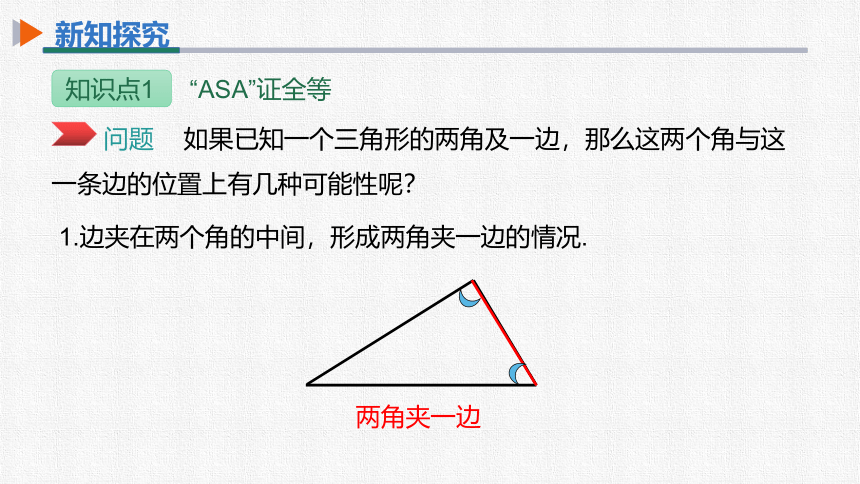
两角夹一边
1.边夹在两个角的中间,形成两角夹一边的情况.
问题 如果已知一个三角形的两角及一边,那么这两个角与这一条边的位置上有几种可能性呢?
新知探究
知识点1 “ASA”证全等
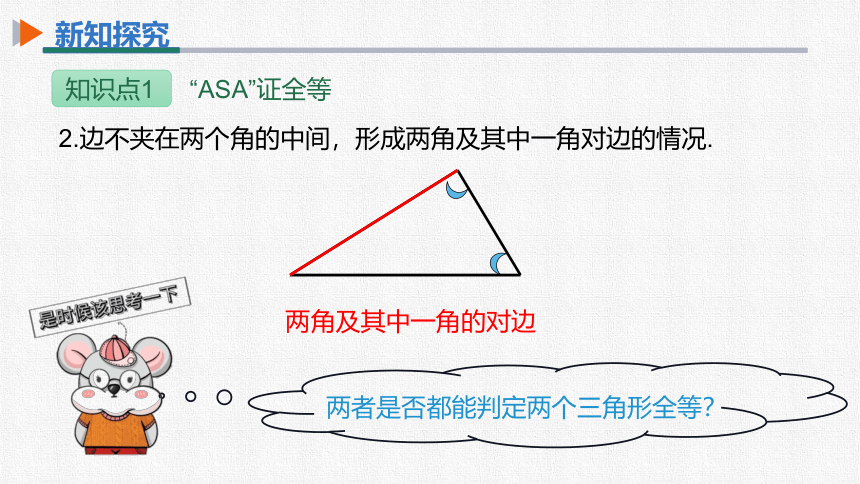
两角及其中一角的对边
两者是否都能判定两个三角形全等?
2.边不夹在两个角的中间,形成两角及其中一角对边的情况.
新知探究
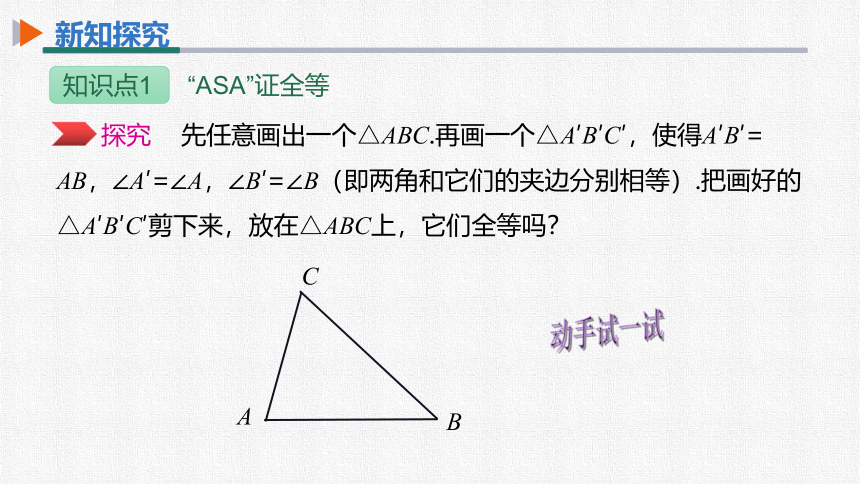
探究 先任意画出一个△ABC.再画一个△A′B′C′,使得A′B′=
AB,∠A′=∠A,∠B′=∠B(即两角和它们的夹边分别相等).把画好的△A′B′C′剪下来,放在△ABC上,它们全等吗?
知识点1 “ASA”证全等
动手试一试
A
C
B
新知探究
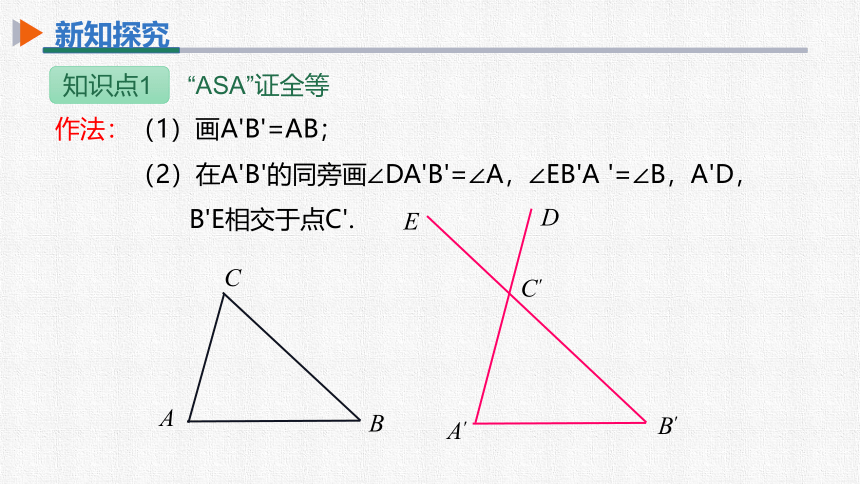
知识点1 “ASA”证全等
作法:(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B'=∠A,∠EB'A '=∠B,A'D,
B'E相交于点C'.
A
C
B
A′
B′
C′
E
D
新知探究
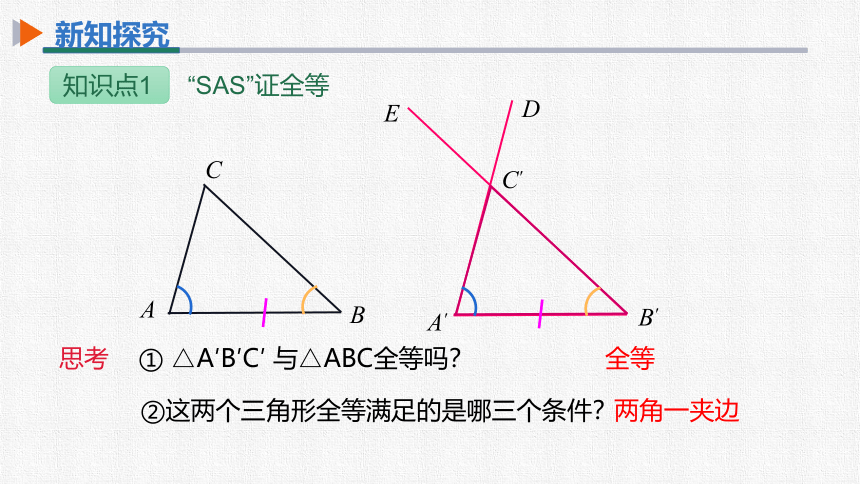
知识点1 “SAS”证全等
思考 ① △A′B′C′ 与△ABC全等吗?
②这两个三角形全等满足的是哪三个条件?
全等
两角一夹边
A
C
B
A′
B′
C′
E
D
新知探究
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
该基本事实可以用来判定两个三角形全等
知识点1 “ASA”证全等
新知探究
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(ASA).
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
该判定定理的几何语言:
注意:必须是两角的夹边
就也是说,三角形的两个角的大小和它们的夹边的大小确定了,这个三角形的形状、大小就确定了.
知识点1 “ASA”证全等
新知探究
知识点1 “ASA”证全等
例 在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
证明:
在△ABC中,∠A+∠B+∠C=180°.
∴∠C=180°-∠A-∠B.
同理 ∠F=180°-∠D-∠E.
【分析】如果能证明∠C=∠F,就可以利用“角边角”证明△ABC和△DEF全等,由三角形内角和定理可以证明∠C=∠F.
A
B
E
D
C
F
新知探究
知识点1 “ASA”证全等
例 在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
∠B=∠E,
BC=EF,
∠C=∠F,
∴△ABC≌△DEF(ASA).
又∠A=∠D,∠B=∠E,
∴∠C=∠F.
在△ABC和△DEF中,
“角角边”也能证明三角形全等?
A
B
E
D
C
F
新知探究
知识点2 “AAS”证全等
问题 已知在△ABC中,∠B=60°,∠C=45°,AB=3cm,你能画出△A′B′C′,使△A′B′C′≌△ABC吗?
联想例1和“ASA”的探究过程,说一说你是怎么画的?
60°
45°
3cm
A
B
C
新知探究
知识点2 “AAS”证全等
因为∠B=60°,∠C=45°,所以∠A=75°,则“AAS”可转化为“ASA”,那么△A′B′C′≌△ABC.
75°
60°
45°
3cm
A
B
C
两角分别相等且其中一组等角的对边相等的两个三角形全等.(可以简写成“角角边”或“AAS”).
新知探究
知识点2 “AAS”证全等
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(AAS).
∠A=∠A′,
∠B=∠B′,
BC=B′C′,
该判定定理的几何语言:
就也是说,三角形的两个角的大小和其中一个角的对边的长度确定了,这个三角形的形状、大小就确定了.
新知探究
知识点2 “AAS”证全等
“ASA”和'AAS”的区别与联系
“S”的意义 书写格式 联系
ASA “S”是两角的夹边 把夹边相等写在两角相等的中间 由三角形的内角和定理可知,“ASA”和“AAS”可以互相转化
AAS “S”是其中一角的对边 把两角相等写在一起,边相等放在最后
跟踪训练
新知探究
如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判别下面的两个三角形是否全等,并说明理由.
解:不全等,因为BC虽然是公共边,但不是对应边.
A
B
C
D
有两角和一边分别相等的两个三角形不一定全等.
新知探究
知识点3 “AAA”不能证全等
思考 三角分别相等的两个三角形全等吗?
不一定全等
假设三个角分别为30°,60°和90°.
新知探究
知识点3 “AAA”不能证全等
判定两个三角形全等的方法
SSS,SAS,ASA,AAS
SSA和AAA不能判定两个三角形全等
课堂小结
三角形的全等的判定(三)(ASA,AAS)
角边角
(SAS)
内容
两角和它们的夹边对应相等的两个三角形全等
已知两角,必须找“夹边”
注意事项
角角边(AAS)
有两角和一边分别相等的两个三角形不一定全等.
内容
注意事项
两角分别相等且其中一组等角的对边相等的两个三角形全等.
判定三角形全等的方法
SSS,SAS,ASA,AAS
课堂训练
1.如图,小明不慎将一块三角形模具打碎为三块,他想配一块与原来一样的三角形模具,为了方便,应该带哪块去商店 ( )
A.1 B.2 C.3 D.三块都带去
3
2
1
A
课堂训练
2.如图,在△ABC和△DCB中,∠ACB=∠DBC,添加一个条件,不能证明△ABC和△DCB全等的是( )
A.∠ABC=∠DCB B.AB=DC C.AC=DB D.∠A=∠D
B
【解析】已知∠ACB=∠DBC,BC=BC,
A:当∠ABC=∠DCB时,可用ASA证明;
B:当AB=DC时,不能证明两三角形全等;
C:当AC=DB时,可用SAS证明;
D:当∠A=∠D时,可用AAS证明.故选B.
课堂训练
3. 如图,AC=AD,∠1=∠2,要使△ABC≌△AED,应添加的条件
是 .(只需写出一个条件即可)
【解析】∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,即∠BAC=∠EAD.
∵AC=AD,
∴当添加∠B=∠E时,可根据“AAS”判断;
当添加∠C=∠D时,可根据“ASA”判断;
当添加AB=AE时,可根据“SAS”判断.
(任选其中一个条件即可).
课堂训练
4.如图,点A、B、D、E在同一条直线上,AB=DE,AC∥DF,BC∥EF.求证:△ABC≌△DEF.
证明:∵AC∥DF,∴∠CAB=∠FDE.
∵BC∥EF,∴∠CBA=∠FED.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
,
,
,
课堂训练
5.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BD=CE.
等边减等边,其差还是等边.
证明:在△ABE与△ACD中,
∴△ABE≌△ACD(ASA).
∴AD=AE.
∴AB-AD=AC-CE,即BD=CE.
,
,
,
课堂训练
6. 如图,AB交CD于点O,在△AOC与△BOD中,有下列三个条件:①OC=OD,②AC=BD,③∠A=∠B.请你在上述三个条件中选择两个为条件,另一个能作为这两个条件推出来的结论,并证明你的结论(只要求写出一种正确的选法).
(1)你选的条件为 、 ,
结论为 ;
(2)证明你的结论.
课堂训练
①OC=OD,②AC=BD,③∠A=∠B.
解:选的条件为①、③ ,结论为②. 证明:在△AOC和△BOD中,
∴△AOC≌△BOD(AAS),
∴AC=BD.
,
,
,
课堂训练
解:选的条件为②、③ ,结论为①.
证明:在△AOC和△BOD中,
∠AOC=∠BOD,
∠A=∠B,
AC=BD,
∴△AOC≌△BOD(AAS),∴OC=OD.
①OC=OD,②AC=BD,③∠A=∠B.
课堂训练
①OC=OD,②AC=BD,③∠A=∠B.
选的条件为①、② ,结论为③,可以吗?
若选的条件为①、② ,
得不到结论③,因为“SSA”不能作
为判定全等的定理.
再结合∠AOC=∠BOD,
课堂训练
7. 如图,在△DAE和△ABC中,D是AC上一点,AD=AB,DE∥AB,∠E=∠C.求证:AE=BC.
证明:∵DE∥AB,
∴∠ADE=∠BAC.
在△ADE和△BAC中,
∴△ADE≌△BAC(AAS),∴AE=BC.
,
,
,
课堂训练
8.如图,点E、C、D、A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.求证:BC=EF.
证明:∵AB∥DF,∴∠B=∠CPD,∠A=∠FDE,
∵∠E=∠CPD.∴∠B=∠E.
在△ABC和△DEF中,
∠B=∠E,
AB=DE,
∠FDE=∠A,
∴△ABC≌△DEF(ASA).∴BC=EF.
课堂训练
9. 如图,在△ABC中,∠ABC=90°,BD⊥AC于点D,点E在DB的延长线上,DE=BC,∠1=∠2,求证:DF=AB.
A
B
C
D
F
E
1
2
等角的余角相等.
证明:∵BD⊥AC,∴∠EDF=90°.∴∠EDF=∠ABC.
∵∠1=∠2,∠1+∠C=90°,∠2+∠E=90°,
∴∠E=∠C.
在△DEF和△BCA中,
∴△DEF≌△BCA(ASA),∴DF=AB.
,
,
,
第十二章 全等三角形
12.2 三角形全等的判定
第3课时 三角形的全等的判定(三)(ASA,AAS)
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.探索并正确理解三角形全等的判定方法“ASA”和“AAS”.
(重点)
2.能熟练利用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.(难点)
新课导入
复习引入
1.回顾我们已经学习过的判定三角形全等的两个定理.
边边边(SSS):三边分别相等的两个三角形全等.
边角边(SAS):两边和它们的夹角分别相等的两个三角形全等.
新课导入
复习引入
2.两判定定理的几何语言:
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
AB=A'B',
BC=B'C',
CA=C'A',
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(SAS).
AB=A'B',
∠B=∠B′,
BC=B′C′,
新课导入
复习引入
3.(1)我们已经总结过的找相等边的方法.
③等边加同边,其和还是等边.
①公共边.
(2)我们已经总结过的找相等角的方法.
①利用平行线可找到相等的角.
②正多边形的边相等.
②对顶角.
③等角加同角,其和还是等角.
④等角减同角,其差还是等角.
⑤等角的补角相等.
⑥正多边形的内角相等.
④等边减同边,其差还是等边.
新课导入
复习引入
4.当两个三角形满足六个条件中的“三个对应条件相等”时,有以下四种情况:
三个角对应相等
三条边对应相等
两条边和一个角对应相等 SAS
SSA
两个角和一条边对应相等
全等
不一定全等
不一定全等
全等
?
新知探究
知识点1 “ASA”证全等
两角夹一边
1.边夹在两个角的中间,形成两角夹一边的情况.
问题 如果已知一个三角形的两角及一边,那么这两个角与这一条边的位置上有几种可能性呢?
新知探究
知识点1 “ASA”证全等
两角及其中一角的对边
两者是否都能判定两个三角形全等?
2.边不夹在两个角的中间,形成两角及其中一角对边的情况.
新知探究
探究 先任意画出一个△ABC.再画一个△A′B′C′,使得A′B′=
AB,∠A′=∠A,∠B′=∠B(即两角和它们的夹边分别相等).把画好的△A′B′C′剪下来,放在△ABC上,它们全等吗?
知识点1 “ASA”证全等
动手试一试
A
C
B
新知探究
知识点1 “ASA”证全等
作法:(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B'=∠A,∠EB'A '=∠B,A'D,
B'E相交于点C'.
A
C
B
A′
B′
C′
E
D
新知探究
知识点1 “SAS”证全等
思考 ① △A′B′C′ 与△ABC全等吗?
②这两个三角形全等满足的是哪三个条件?
全等
两角一夹边
A
C
B
A′
B′
C′
E
D
新知探究
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
该基本事实可以用来判定两个三角形全等
知识点1 “ASA”证全等
新知探究
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(ASA).
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
该判定定理的几何语言:
注意:必须是两角的夹边
就也是说,三角形的两个角的大小和它们的夹边的大小确定了,这个三角形的形状、大小就确定了.
知识点1 “ASA”证全等
新知探究
知识点1 “ASA”证全等
例 在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
证明:
在△ABC中,∠A+∠B+∠C=180°.
∴∠C=180°-∠A-∠B.
同理 ∠F=180°-∠D-∠E.
【分析】如果能证明∠C=∠F,就可以利用“角边角”证明△ABC和△DEF全等,由三角形内角和定理可以证明∠C=∠F.
A
B
E
D
C
F
新知探究
知识点1 “ASA”证全等
例 在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
∠B=∠E,
BC=EF,
∠C=∠F,
∴△ABC≌△DEF(ASA).
又∠A=∠D,∠B=∠E,
∴∠C=∠F.
在△ABC和△DEF中,
“角角边”也能证明三角形全等?
A
B
E
D
C
F
新知探究
知识点2 “AAS”证全等
问题 已知在△ABC中,∠B=60°,∠C=45°,AB=3cm,你能画出△A′B′C′,使△A′B′C′≌△ABC吗?
联想例1和“ASA”的探究过程,说一说你是怎么画的?
60°
45°
3cm
A
B
C
新知探究
知识点2 “AAS”证全等
因为∠B=60°,∠C=45°,所以∠A=75°,则“AAS”可转化为“ASA”,那么△A′B′C′≌△ABC.
75°
60°
45°
3cm
A
B
C
两角分别相等且其中一组等角的对边相等的两个三角形全等.(可以简写成“角角边”或“AAS”).
新知探究
知识点2 “AAS”证全等
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(AAS).
∠A=∠A′,
∠B=∠B′,
BC=B′C′,
该判定定理的几何语言:
就也是说,三角形的两个角的大小和其中一个角的对边的长度确定了,这个三角形的形状、大小就确定了.
新知探究
知识点2 “AAS”证全等
“ASA”和'AAS”的区别与联系
“S”的意义 书写格式 联系
ASA “S”是两角的夹边 把夹边相等写在两角相等的中间 由三角形的内角和定理可知,“ASA”和“AAS”可以互相转化
AAS “S”是其中一角的对边 把两角相等写在一起,边相等放在最后
跟踪训练
新知探究
如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判别下面的两个三角形是否全等,并说明理由.
解:不全等,因为BC虽然是公共边,但不是对应边.
A
B
C
D
有两角和一边分别相等的两个三角形不一定全等.
新知探究
知识点3 “AAA”不能证全等
思考 三角分别相等的两个三角形全等吗?
不一定全等
假设三个角分别为30°,60°和90°.
新知探究
知识点3 “AAA”不能证全等
判定两个三角形全等的方法
SSS,SAS,ASA,AAS
SSA和AAA不能判定两个三角形全等
课堂小结
三角形的全等的判定(三)(ASA,AAS)
角边角
(SAS)
内容
两角和它们的夹边对应相等的两个三角形全等
已知两角,必须找“夹边”
注意事项
角角边(AAS)
有两角和一边分别相等的两个三角形不一定全等.
内容
注意事项
两角分别相等且其中一组等角的对边相等的两个三角形全等.
判定三角形全等的方法
SSS,SAS,ASA,AAS
课堂训练
1.如图,小明不慎将一块三角形模具打碎为三块,他想配一块与原来一样的三角形模具,为了方便,应该带哪块去商店 ( )
A.1 B.2 C.3 D.三块都带去
3
2
1
A
课堂训练
2.如图,在△ABC和△DCB中,∠ACB=∠DBC,添加一个条件,不能证明△ABC和△DCB全等的是( )
A.∠ABC=∠DCB B.AB=DC C.AC=DB D.∠A=∠D
B
【解析】已知∠ACB=∠DBC,BC=BC,
A:当∠ABC=∠DCB时,可用ASA证明;
B:当AB=DC时,不能证明两三角形全等;
C:当AC=DB时,可用SAS证明;
D:当∠A=∠D时,可用AAS证明.故选B.
课堂训练
3. 如图,AC=AD,∠1=∠2,要使△ABC≌△AED,应添加的条件
是 .(只需写出一个条件即可)
【解析】∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,即∠BAC=∠EAD.
∵AC=AD,
∴当添加∠B=∠E时,可根据“AAS”判断;
当添加∠C=∠D时,可根据“ASA”判断;
当添加AB=AE时,可根据“SAS”判断.
(任选其中一个条件即可).
课堂训练
4.如图,点A、B、D、E在同一条直线上,AB=DE,AC∥DF,BC∥EF.求证:△ABC≌△DEF.
证明:∵AC∥DF,∴∠CAB=∠FDE.
∵BC∥EF,∴∠CBA=∠FED.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
,
,
,
课堂训练
5.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BD=CE.
等边减等边,其差还是等边.
证明:在△ABE与△ACD中,
∴△ABE≌△ACD(ASA).
∴AD=AE.
∴AB-AD=AC-CE,即BD=CE.
,
,
,
课堂训练
6. 如图,AB交CD于点O,在△AOC与△BOD中,有下列三个条件:①OC=OD,②AC=BD,③∠A=∠B.请你在上述三个条件中选择两个为条件,另一个能作为这两个条件推出来的结论,并证明你的结论(只要求写出一种正确的选法).
(1)你选的条件为 、 ,
结论为 ;
(2)证明你的结论.
课堂训练
①OC=OD,②AC=BD,③∠A=∠B.
解:选的条件为①、③ ,结论为②. 证明:在△AOC和△BOD中,
∴△AOC≌△BOD(AAS),
∴AC=BD.
,
,
,
课堂训练
解:选的条件为②、③ ,结论为①.
证明:在△AOC和△BOD中,
∠AOC=∠BOD,
∠A=∠B,
AC=BD,
∴△AOC≌△BOD(AAS),∴OC=OD.
①OC=OD,②AC=BD,③∠A=∠B.
课堂训练
①OC=OD,②AC=BD,③∠A=∠B.
选的条件为①、② ,结论为③,可以吗?
若选的条件为①、② ,
得不到结论③,因为“SSA”不能作
为判定全等的定理.
再结合∠AOC=∠BOD,
课堂训练
7. 如图,在△DAE和△ABC中,D是AC上一点,AD=AB,DE∥AB,∠E=∠C.求证:AE=BC.
证明:∵DE∥AB,
∴∠ADE=∠BAC.
在△ADE和△BAC中,
∴△ADE≌△BAC(AAS),∴AE=BC.
,
,
,
课堂训练
8.如图,点E、C、D、A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.求证:BC=EF.
证明:∵AB∥DF,∴∠B=∠CPD,∠A=∠FDE,
∵∠E=∠CPD.∴∠B=∠E.
在△ABC和△DEF中,
∠B=∠E,
AB=DE,
∠FDE=∠A,
∴△ABC≌△DEF(ASA).∴BC=EF.
课堂训练
9. 如图,在△ABC中,∠ABC=90°,BD⊥AC于点D,点E在DB的延长线上,DE=BC,∠1=∠2,求证:DF=AB.
A
B
C
D
F
E
1
2
等角的余角相等.
证明:∵BD⊥AC,∴∠EDF=90°.∴∠EDF=∠ABC.
∵∠1=∠2,∠1+∠C=90°,∠2+∠E=90°,
∴∠E=∠C.
在△DEF和△BCA中,
∴△DEF≌△BCA(ASA),∴DF=AB.
,
,
,
