数学七年级下青岛版9.3平行线的性质课件1
文档属性
| 名称 | 数学七年级下青岛版9.3平行线的性质课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 162.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-26 08:48:21 | ||
图片预览






文档简介
课件18张PPT。平行线的性质与判定复习回顾平行线的性质1:
两条平行线被第三条直线所截,同位角相等.
简写为:两直线平行,同位角相等.
平行线的性质2:
两条平行线被第三条直线所截,内错角相等.
简写为:两直线平行,内错角相等.
平行线的性质3:
两条平行线被第三条直线所截,同旁内角互补.
简写为:两直线平行,同旁内角互补.
图形语言符号语言文字语言同位角内错角同旁内角∵a∥b
∴∠2=∠3两直线平行
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
122324))))))abababccc∵a∥b
∴∠1=∠2∵a∥b
∴∠4+∠2=180°平行线的性质图形语言符号语言文字语言同位角内错角同旁内角∵∠2=∠3
∴a∥b
同位角相等
两直线平行内错角相等
两直线平行同旁内角互补
两直线平行122324))))))abababccc∵∠1=∠2
∴a∥b∵∠4+∠2=180°
∴a∥b
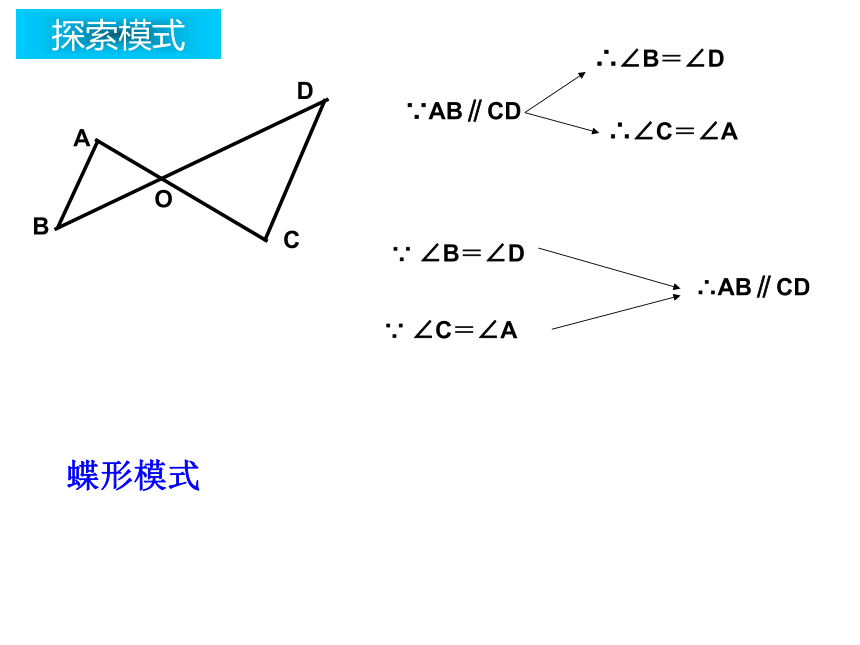
平行线的判定两直线平行同位角相等内错角相等同旁内角互补线的关系角的关系判定性质平行线的性质和平行线的判定方法的 区 别 与 联 系 归纳与总结F 形C 形Z形复习模式探索模式∵AB∥CD∴AB∥CD蝶形模式蝶形模式探索模式1.如图所示:AD∥BC,∠A=∠C,试说明AB∥DC.解:∵AD//BC(已知)∴ ∠A=∠ABF(两直线平行,内错角相等)又∵∠A=∠C (已知)∴ ∠ABF=∠C(等量代换)∴ AB∥DC(同位角相等,两直线平行)应用模式变式:如图所示:AD∥BC,∠A=∠C,试说明AB∥DC .AEDFBCAD∥BCAB∥DC解:∵ AB//DC(已知)∴ ∠C=∠ABF(两直线平行,同位角相等)又∵∠A=∠C (已知)∴ ∠ABF=∠A∴ AD∥BC(内错角相等,两直线平行)2.如图所示:3.如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,试问:∠A与∠F相等吗?请说出你的理由。
∵DE∥BC∴DE∥BC塔形模式探究模式探究模式问题3、已知:如图,?1=?2=?B,EF∥AB。
问:?3和?C有什么数量关系?为什么?填空:∵?1=?B( )
∴DE∥BC( )
∴?2=?C( )
∵EF∥AB( )
∴?B=?3( )
又∵?2=?B( )
∴?3=?C( )
应用模式
1、 已知:CD∥EF, ∠1= ∠2,求证: ∠AGD= ∠ACB。证明:∵CD ∥EF ( )(3)已知:∠AGD= ∠ACB
∠1= ∠2.
求证: CD∥EF.∴ ∠ AGD= ∠ ACB ( )∴DG ∥BC ( )∴ ∠1= ∠3 ( )∵ ∠1= ∠2 ( )∴ ∠2= ∠3 ( )应用模式课堂小结:
1、通过习题你有何收获?
要判定两条直线平行,可以运用哪些公理或定理?
要判定两个角相等或互补,可以运用哪些公理或定理?
2、思想方法:
分析问题的方法:
由已知看可知,扩大已知面。
由未知想需知,明确解题方向
识图的方法:
在定理图形中提炼基本图形,
在解题时把复杂图形分解为基本图形 结束寄语严格性之于数学家,犹如道德之于人.
由“因”导“果”,言必有据.是初学证明者谨记和遵循的原则.
两条平行线被第三条直线所截,同位角相等.
简写为:两直线平行,同位角相等.
平行线的性质2:
两条平行线被第三条直线所截,内错角相等.
简写为:两直线平行,内错角相等.
平行线的性质3:
两条平行线被第三条直线所截,同旁内角互补.
简写为:两直线平行,同旁内角互补.
图形语言符号语言文字语言同位角内错角同旁内角∵a∥b
∴∠2=∠3两直线平行
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
122324))))))abababccc∵a∥b
∴∠1=∠2∵a∥b
∴∠4+∠2=180°平行线的性质图形语言符号语言文字语言同位角内错角同旁内角∵∠2=∠3
∴a∥b
同位角相等
两直线平行内错角相等
两直线平行同旁内角互补
两直线平行122324))))))abababccc∵∠1=∠2
∴a∥b∵∠4+∠2=180°
∴a∥b
平行线的判定两直线平行同位角相等内错角相等同旁内角互补线的关系角的关系判定性质平行线的性质和平行线的判定方法的 区 别 与 联 系 归纳与总结F 形C 形Z形复习模式探索模式∵AB∥CD∴AB∥CD蝶形模式蝶形模式探索模式1.如图所示:AD∥BC,∠A=∠C,试说明AB∥DC.解:∵AD//BC(已知)∴ ∠A=∠ABF(两直线平行,内错角相等)又∵∠A=∠C (已知)∴ ∠ABF=∠C(等量代换)∴ AB∥DC(同位角相等,两直线平行)应用模式变式:如图所示:AD∥BC,∠A=∠C,试说明AB∥DC .AEDFBCAD∥BCAB∥DC解:∵ AB//DC(已知)∴ ∠C=∠ABF(两直线平行,同位角相等)又∵∠A=∠C (已知)∴ ∠ABF=∠A∴ AD∥BC(内错角相等,两直线平行)2.如图所示:3.如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,试问:∠A与∠F相等吗?请说出你的理由。
∵DE∥BC∴DE∥BC塔形模式探究模式探究模式问题3、已知:如图,?1=?2=?B,EF∥AB。
问:?3和?C有什么数量关系?为什么?填空:∵?1=?B( )
∴DE∥BC( )
∴?2=?C( )
∵EF∥AB( )
∴?B=?3( )
又∵?2=?B( )
∴?3=?C( )
应用模式
1、 已知:CD∥EF, ∠1= ∠2,求证: ∠AGD= ∠ACB。证明:∵CD ∥EF ( )(3)已知:∠AGD= ∠ACB
∠1= ∠2.
求证: CD∥EF.∴ ∠ AGD= ∠ ACB ( )∴DG ∥BC ( )∴ ∠1= ∠3 ( )∵ ∠1= ∠2 ( )∴ ∠2= ∠3 ( )应用模式课堂小结:
1、通过习题你有何收获?
要判定两条直线平行,可以运用哪些公理或定理?
要判定两个角相等或互补,可以运用哪些公理或定理?
2、思想方法:
分析问题的方法:
由已知看可知,扩大已知面。
由未知想需知,明确解题方向
识图的方法:
在定理图形中提炼基本图形,
在解题时把复杂图形分解为基本图形 结束寄语严格性之于数学家,犹如道德之于人.
由“因”导“果”,言必有据.是初学证明者谨记和遵循的原则.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
