初中数学人教版八上同步课件:12.2第4课时三角形全等的判定(四)(37张PPT)
文档属性
| 名称 | 初中数学人教版八上同步课件:12.2第4课时三角形全等的判定(四)(37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 21:58:40 | ||
图片预览








文档简介
(共37张PPT)
第十二章 全等三角形
12.2 三角形全等的判定
第4课时 三角形的全等的判定(四)(HL)
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.探索并理解直角三角形全等的判定方法“HL”.(难点)
2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.(重点)
新课导入
复习引入
1.回顾我们已经学习过的判定三角形全等的四个定理.
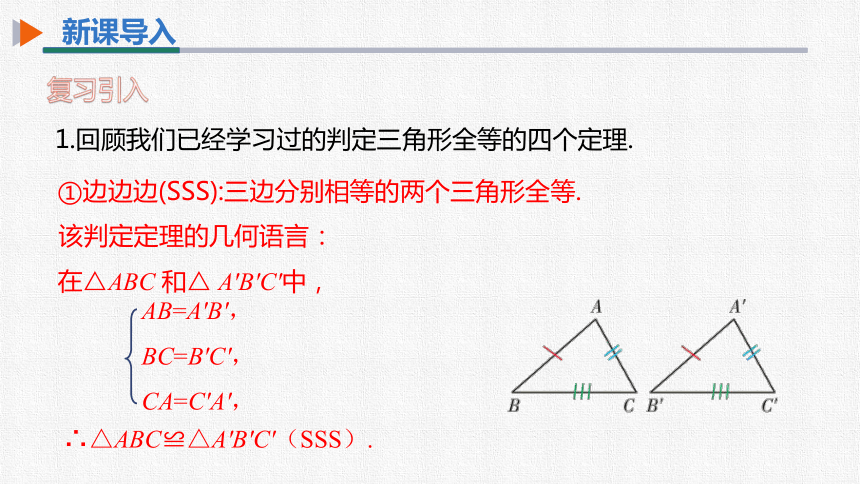
①边边边(SSS):三边分别相等的两个三角形全等.
该判定定理的几何语言:
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
AB=A'B',
BC=B'C',
CA=C'A',
新课导入
复习引入
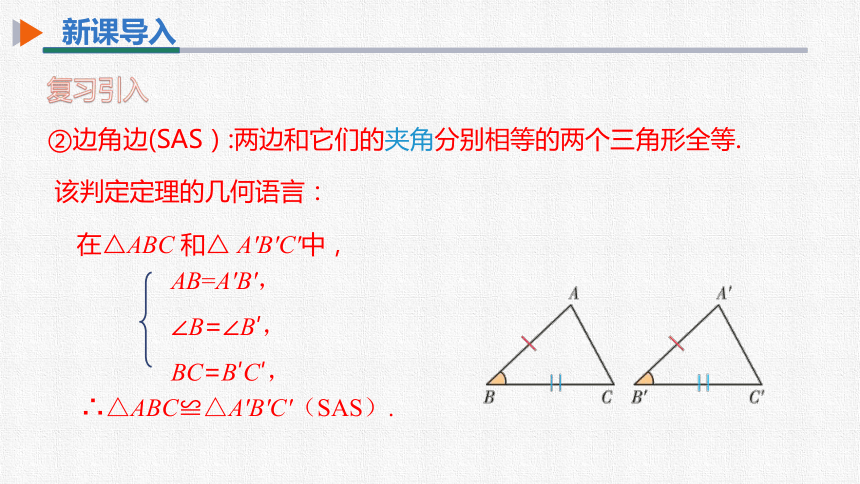
②边角边(SAS):两边和它们的夹角分别相等的两个三角形全等.
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(SAS).
AB=A'B',
∠B=∠B′,
BC=B′C′,
该判定定理的几何语言:
新课导入
复习引入
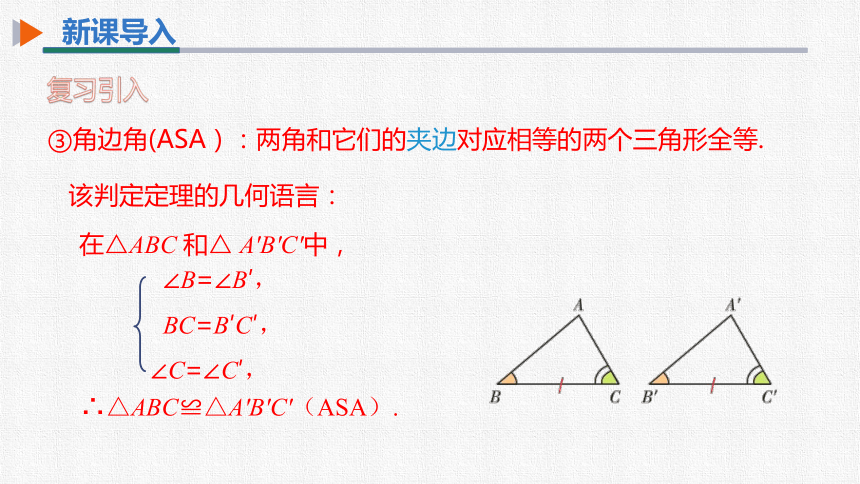
③角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(ASA).
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
该判定定理的几何语言:
新课导入
复习引入
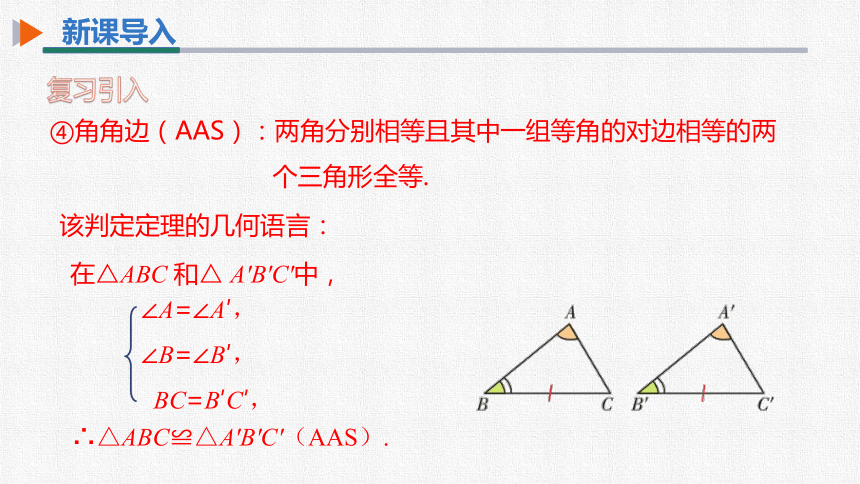
④角角边(AAS):两角分别相等且其中一组等角的对边相等的两
个三角形全等.
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(AAS).
∠A=∠A′,
∠B=∠B′,
BC=B′C′,
该判定定理的几何语言:
新课导入
复习引入
2.我们已经总结过的找相等边的方法.
③等边加(减)同边,其和(差)还是等边.
①公共边.
②正多边形的边相等.
④等边减等边,其差还是等边.
新课导入
复习引入
3.我们已经总结过的找相等角的方法.
①利用平行线找同位角或内错角.
②对顶角.
③等角加(减)同角,其和(差)还是等角.
④等角的补(余)角相等.
⑤正多边形的内角相等.
新知探究
知识点 “HL”证全等
思考 对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了?
结合刚才复习的判定三角形全等的方法想一想吧!
新知探究
C′
A
B
C
B′
A′
┐
┐
1.对于两个直角三角形中,满足一直角边及其相对的锐角对应相等,这两个直角三角形全等吗?你的判定根据是什么?
全等,根据“AAS”.
知识点 “HL”证全等
新知探究
C′
A
B
C
B′
A′
┐
┐
2.对于两个直角三角形中,满足一直角边及其相邻的锐角对应相等,这两个直角三角形全等吗?你的判定根据是什么?
全等,根据“ASA”.
知识点 “HL”证全等
新知探究
C′
A
B
C
B′
A′
┐
┐
3.对于两个直角三角形中,满足两直角边对应相等,这两个直角三角形全等吗?你的判定根据是什么?
全等,根据“SAS”.
知识点 “HL”证全等
新知探究
C′
A
B
C
B′
A′
┐
┐
4.对于两个直角三角形中,满足斜边和一锐角对应相等,这两个直角三角形全等吗?你的判定根据是什么?
全等,根据“AAS”.
知识点 “HL”证全等
新知探究
C′
A
B
C
B′
A′
┐
┐
我们知道,证明三角形全等不存在SSA定理.那么满足该条件的直角三角形是不是就不全等呢?
知识点 “HL”证全等
对于两个直角三角形中,满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
新知探究
探究 任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A′B′C′,使得∠C′=90°,B′C′=BC,A′B′=AB.把画好的Rt△A′B′C′剪下来,放在Rt△ABC上,它们全等吗?
动手试一试
知识点 “HL”证全等
A
B
C
新知探究
作法:(1)画∠MC′N=90°;
M
C′
N
A
B
C
(2)在射线C′M上截取B′C′=BC;
B′
知识点 “HL”证全等
新知探究
作法:(3)以点B′为圆心,AB长为半径画弧, 交射线C′N于点A′;
(4)连接A′B′.
M
C′
N
A
B
C
B′
A′
知识点 “HL”证全等
新知探究
思考 ① △A′B′C′ 与△ABC全等吗?
②这两个三角形全等满足的是哪三个条件?
全等
直角、斜边和一条直角边
M
C′
N
A
B
C
B′
A′
知识点 “HL”证全等
新知探究
斜边和一条直角边分别相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
该基本事实可以用来判定两个直角三角形全等
知识点 “HL”证全等
新知探究
在Rt△ABC 和Rt△ A'B'C'中,
∴Rt△ABC≌Rt△A'B'C'(HL).
AC=A′C′,
BC=B′C′,
该判定定理的几何语言:
用“HL”证明两个直角三角形全等的注意事项:
C′
A
B
C
B′
A′
┐
┐
①应用“HL”的前提条件是在直角三角形中;
②书写时两个三角形符号前面要加上“Rt”;
③书写条件时,先写斜边(H),再写直角边(L).
知识点 “HL”证全等
新知探究
知识点 “HL”证全等
已知条件 需寻找的条件 判定方法
一锐角对应相等 直角与已知锐角的夹边对应相等
与锐角(或直角)的对边对应相等
斜边对应相等 一直角边对应相等
一锐角对应相等
一直角边对应相等 斜边对应相等
已知边相邻的锐角对应相等
已知边所对的锐角对应相等
ASA
AAS
HL
AAS
HL
ASA
AAS
新知探究
例 如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证:BC=AD.
证明:∵AC⊥BC,BD⊥AD,
∴∠C与∠D都是直角.
在Rt△ABC和Rt△BAD中,
AB=BA,
AC=BD,
∴Rt△ABC≌Rt△BAD(HL).∴BC=AD.
D
A
B
C
知识点 “HL”证全等
跟踪训练
新知探究
如图,∠ACB=∠ADB=90°,要证明△ABC≌ △BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由.
(1) ( )
(2) ( )
(3) ( )
(4) ( )
D
A
B
C
AD=BC
∠ DAB= ∠ CBA
BD=AC
∠ DBA= ∠ CAB
HL
HL
AAS
AAS
课堂小结
三角形的全等的判定(四)(HL)
斜边、直角边
(HL)
内容
斜边和一条直角边分别相等的两个直角三角形全等
前提条件是在直角三角形中;书写时两个三角形符号前面要加上“Rt”;书写条件时,先写斜边(H),再写直角边(L).
注意
事项
根据已知条件选择适合证明两个直角三角形全等的方法
隐含条件:
两直角相等
课堂训练
1.如图,在△ABC中,AB=AC,AD⊥BC ,以下结论:
(1)△ABD≌△ACD;(2)BD=CD;(3)∠B=∠C;(4) AD是△ABC的一条角平分线.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
课堂训练
2. 已知在△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,下列条件中,不一定能得到△ABC≌△A′B′C′的是( )
A.BC=B′C′ B.∠A=∠A′
C.∠C=∠C′ D.∠B=∠B′=90°
C
【解析】∵AB=A′B′,AC=A′C′,
∴A.由BC=B′C′可根据“SSS”判定;
B.由∠A=∠A′可根据“SAS”判定;
C.由∠C=∠C′不可判定,因为没有“SSA”;
D.由∠B=∠B′=90°可根据“HL”判定.故选C.
课堂训练
3. 如图,在△ABC和△ADC中,AB⊥BC,AD⊥DC,只需添加一个条件即可证明△ABC≌△ADC,这个条件可以是 .(写出一个即可)
【解析】∵AB⊥BC,AD⊥DC,∴∠B=∠D=90°.
∵AC=AC(公共边),∴当添加CB=CD或AB=AD时,则可根据“HL”判断;当添加∠ACB=∠ACD或∠BAC=∠DAC时,则可根据“AAS”判断.故答案为CB=CD或AB=AD或∠ACB=∠ACD或∠BAC=∠DAC(选择其中一个条件即可).
课堂训练
4.如图,在四边形ABCD中,点E,F分别在AB,CD上,且AE=CF,分别过点A,C向EF作垂线,垂足分别为点G,H,且AG=CH.求证:AB∥CD.
证明:∵AG⊥GH,CH⊥GH,∴∠G=∠H=90°.
在Rt△AGE和Rt△CHF中,
∴Rt△AGE≌Rt△CHF(HL).
,
,
课堂训练
4.如图,在四边形ABCD中,点E,F分别在AB,CD上,且AE=CF,分别过点A,C向EF作垂线,垂足分别为点G,H,且AG=CH.求证:AB∥CD.
∴∠AEG=∠CFH.
∵∠AEG=∠BEF,
∴∠BEF=∠CFH.
∴AB∥CD.
课堂训练
5. 如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M,N,且BM=AN.
(1)求证△AMB≌△CNA;
证明:∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°.
在Rt△AMB和Rt△CNA中,
∴Rt△AMB≌Rt△CNA(HL);
,
,
课堂训练
5. 如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M,N,且BM=AN.
(2)求证∠BAC=90°.
解:由(1),知Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN.
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°.
∴∠BAC=180°﹣90°=90°.
课堂训练
6.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,∴∠ADB=∠AFB=90°.
在Rt△ADC和Rt△AFE中,
AD=AF,
AC=AE,
∴Rt△ADC≌Rt△AFE(HL).∴CD=EF.
课堂训练
6.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
在Rt△ABD和Rt△ABF中,
AD=AF,
AB=AB,
∴Rt△ABD≌Rt△ABF(HL).∴BD=BF.
∴BD-CD=BF-EF,即BC=BE.
课堂训练
7.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E ,AD,CE交于点H,已知EH=EB=3,AE=4,求CH的长.
证明:∵AD⊥BC于点D,CE⊥AB于点E ,∴∠AEH=∠CEB=∠CDH=90°.
又∠AHE=∠CHD,∴∠EAH=∠ECB.
在△EAH和△ECB中,
∠EAH=∠BCE,
∠AEH=∠CEB,
EH=EB,
课堂训练
7.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E ,AD,CE交于点H,已知EH=EB=3,AE=4,求CH的长.
∴△EAH≌△ECB(AAS).
∴AE=CE,则CE=4.
∴CH=CE-EH=4-3=1.
“HL”是直角三角形独有的判定方法,但直角三角形的判定方法很多,判定时,应抓住“直角”这个隐含条件,选择合适的方法求证.
课堂训练
8.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P,Q两点同时出发,运动多少分钟后,△CAP与△PQB全等?
解:CA⊥AB于点A, DB⊥AB于点B ,
∴∠A=∠B=90°.
设运动x分钟后,△CAP与△PQB全等,则BP=xm , BQ=2xm,AP=(12-x)m.分两种情况:
①若BP=AC ,则x=4,∴AP=12-4=8(m) , BQ=8m, ∴AP=BQ ,此时,△CAP≌△PBQ(SAS);
课堂训练
8.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P,Q两点同时出发,运动多少分钟后,△CAP与△PQB全等?
②若BP=AP ,则12-x=x,解得x=6 , 则BQ=12m≠AC,
此时,△CAP与△PBQ不全等.
综上所示,运动4分钟后,△CAP与△PQB全等.
判定三角形全等的关键是找对应边和对应角,由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.
第十二章 全等三角形
12.2 三角形全等的判定
第4课时 三角形的全等的判定(四)(HL)
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.探索并理解直角三角形全等的判定方法“HL”.(难点)
2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.(重点)
新课导入
复习引入
1.回顾我们已经学习过的判定三角形全等的四个定理.
①边边边(SSS):三边分别相等的两个三角形全等.
该判定定理的几何语言:
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
AB=A'B',
BC=B'C',
CA=C'A',
新课导入
复习引入
②边角边(SAS):两边和它们的夹角分别相等的两个三角形全等.
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(SAS).
AB=A'B',
∠B=∠B′,
BC=B′C′,
该判定定理的几何语言:
新课导入
复习引入
③角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(ASA).
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
该判定定理的几何语言:
新课导入
复习引入
④角角边(AAS):两角分别相等且其中一组等角的对边相等的两
个三角形全等.
在△ABC 和△ A'B'C'中,
∴△ABC≌△A'B'C'(AAS).
∠A=∠A′,
∠B=∠B′,
BC=B′C′,
该判定定理的几何语言:
新课导入
复习引入
2.我们已经总结过的找相等边的方法.
③等边加(减)同边,其和(差)还是等边.
①公共边.
②正多边形的边相等.
④等边减等边,其差还是等边.
新课导入
复习引入
3.我们已经总结过的找相等角的方法.
①利用平行线找同位角或内错角.
②对顶角.
③等角加(减)同角,其和(差)还是等角.
④等角的补(余)角相等.
⑤正多边形的内角相等.
新知探究
知识点 “HL”证全等
思考 对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了?
结合刚才复习的判定三角形全等的方法想一想吧!
新知探究
C′
A
B
C
B′
A′
┐
┐
1.对于两个直角三角形中,满足一直角边及其相对的锐角对应相等,这两个直角三角形全等吗?你的判定根据是什么?
全等,根据“AAS”.
知识点 “HL”证全等
新知探究
C′
A
B
C
B′
A′
┐
┐
2.对于两个直角三角形中,满足一直角边及其相邻的锐角对应相等,这两个直角三角形全等吗?你的判定根据是什么?
全等,根据“ASA”.
知识点 “HL”证全等
新知探究
C′
A
B
C
B′
A′
┐
┐
3.对于两个直角三角形中,满足两直角边对应相等,这两个直角三角形全等吗?你的判定根据是什么?
全等,根据“SAS”.
知识点 “HL”证全等
新知探究
C′
A
B
C
B′
A′
┐
┐
4.对于两个直角三角形中,满足斜边和一锐角对应相等,这两个直角三角形全等吗?你的判定根据是什么?
全等,根据“AAS”.
知识点 “HL”证全等
新知探究
C′
A
B
C
B′
A′
┐
┐
我们知道,证明三角形全等不存在SSA定理.那么满足该条件的直角三角形是不是就不全等呢?
知识点 “HL”证全等
对于两个直角三角形中,满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
新知探究
探究 任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A′B′C′,使得∠C′=90°,B′C′=BC,A′B′=AB.把画好的Rt△A′B′C′剪下来,放在Rt△ABC上,它们全等吗?
动手试一试
知识点 “HL”证全等
A
B
C
新知探究
作法:(1)画∠MC′N=90°;
M
C′
N
A
B
C
(2)在射线C′M上截取B′C′=BC;
B′
知识点 “HL”证全等
新知探究
作法:(3)以点B′为圆心,AB长为半径画弧, 交射线C′N于点A′;
(4)连接A′B′.
M
C′
N
A
B
C
B′
A′
知识点 “HL”证全等
新知探究
思考 ① △A′B′C′ 与△ABC全等吗?
②这两个三角形全等满足的是哪三个条件?
全等
直角、斜边和一条直角边
M
C′
N
A
B
C
B′
A′
知识点 “HL”证全等
新知探究
斜边和一条直角边分别相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
该基本事实可以用来判定两个直角三角形全等
知识点 “HL”证全等
新知探究
在Rt△ABC 和Rt△ A'B'C'中,
∴Rt△ABC≌Rt△A'B'C'(HL).
AC=A′C′,
BC=B′C′,
该判定定理的几何语言:
用“HL”证明两个直角三角形全等的注意事项:
C′
A
B
C
B′
A′
┐
┐
①应用“HL”的前提条件是在直角三角形中;
②书写时两个三角形符号前面要加上“Rt”;
③书写条件时,先写斜边(H),再写直角边(L).
知识点 “HL”证全等
新知探究
知识点 “HL”证全等
已知条件 需寻找的条件 判定方法
一锐角对应相等 直角与已知锐角的夹边对应相等
与锐角(或直角)的对边对应相等
斜边对应相等 一直角边对应相等
一锐角对应相等
一直角边对应相等 斜边对应相等
已知边相邻的锐角对应相等
已知边所对的锐角对应相等
ASA
AAS
HL
AAS
HL
ASA
AAS
新知探究
例 如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证:BC=AD.
证明:∵AC⊥BC,BD⊥AD,
∴∠C与∠D都是直角.
在Rt△ABC和Rt△BAD中,
AB=BA,
AC=BD,
∴Rt△ABC≌Rt△BAD(HL).∴BC=AD.
D
A
B
C
知识点 “HL”证全等
跟踪训练
新知探究
如图,∠ACB=∠ADB=90°,要证明△ABC≌ △BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由.
(1) ( )
(2) ( )
(3) ( )
(4) ( )
D
A
B
C
AD=BC
∠ DAB= ∠ CBA
BD=AC
∠ DBA= ∠ CAB
HL
HL
AAS
AAS
课堂小结
三角形的全等的判定(四)(HL)
斜边、直角边
(HL)
内容
斜边和一条直角边分别相等的两个直角三角形全等
前提条件是在直角三角形中;书写时两个三角形符号前面要加上“Rt”;书写条件时,先写斜边(H),再写直角边(L).
注意
事项
根据已知条件选择适合证明两个直角三角形全等的方法
隐含条件:
两直角相等
课堂训练
1.如图,在△ABC中,AB=AC,AD⊥BC ,以下结论:
(1)△ABD≌△ACD;(2)BD=CD;(3)∠B=∠C;(4) AD是△ABC的一条角平分线.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
课堂训练
2. 已知在△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,下列条件中,不一定能得到△ABC≌△A′B′C′的是( )
A.BC=B′C′ B.∠A=∠A′
C.∠C=∠C′ D.∠B=∠B′=90°
C
【解析】∵AB=A′B′,AC=A′C′,
∴A.由BC=B′C′可根据“SSS”判定;
B.由∠A=∠A′可根据“SAS”判定;
C.由∠C=∠C′不可判定,因为没有“SSA”;
D.由∠B=∠B′=90°可根据“HL”判定.故选C.
课堂训练
3. 如图,在△ABC和△ADC中,AB⊥BC,AD⊥DC,只需添加一个条件即可证明△ABC≌△ADC,这个条件可以是 .(写出一个即可)
【解析】∵AB⊥BC,AD⊥DC,∴∠B=∠D=90°.
∵AC=AC(公共边),∴当添加CB=CD或AB=AD时,则可根据“HL”判断;当添加∠ACB=∠ACD或∠BAC=∠DAC时,则可根据“AAS”判断.故答案为CB=CD或AB=AD或∠ACB=∠ACD或∠BAC=∠DAC(选择其中一个条件即可).
课堂训练
4.如图,在四边形ABCD中,点E,F分别在AB,CD上,且AE=CF,分别过点A,C向EF作垂线,垂足分别为点G,H,且AG=CH.求证:AB∥CD.
证明:∵AG⊥GH,CH⊥GH,∴∠G=∠H=90°.
在Rt△AGE和Rt△CHF中,
∴Rt△AGE≌Rt△CHF(HL).
,
,
课堂训练
4.如图,在四边形ABCD中,点E,F分别在AB,CD上,且AE=CF,分别过点A,C向EF作垂线,垂足分别为点G,H,且AG=CH.求证:AB∥CD.
∴∠AEG=∠CFH.
∵∠AEG=∠BEF,
∴∠BEF=∠CFH.
∴AB∥CD.
课堂训练
5. 如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M,N,且BM=AN.
(1)求证△AMB≌△CNA;
证明:∵BM⊥直线l,CN⊥直线l,
∴∠AMB=∠CNA=90°.
在Rt△AMB和Rt△CNA中,
∴Rt△AMB≌Rt△CNA(HL);
,
,
课堂训练
5. 如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M,N,且BM=AN.
(2)求证∠BAC=90°.
解:由(1),知Rt△AMB≌Rt△CNA,
∴∠BAM=∠ACN.
∵∠CAN+∠ACN=90°,
∴∠CAN+∠BAM=90°.
∴∠BAC=180°﹣90°=90°.
课堂训练
6.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,∴∠ADB=∠AFB=90°.
在Rt△ADC和Rt△AFE中,
AD=AF,
AC=AE,
∴Rt△ADC≌Rt△AFE(HL).∴CD=EF.
课堂训练
6.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
在Rt△ABD和Rt△ABF中,
AD=AF,
AB=AB,
∴Rt△ABD≌Rt△ABF(HL).∴BD=BF.
∴BD-CD=BF-EF,即BC=BE.
课堂训练
7.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E ,AD,CE交于点H,已知EH=EB=3,AE=4,求CH的长.
证明:∵AD⊥BC于点D,CE⊥AB于点E ,∴∠AEH=∠CEB=∠CDH=90°.
又∠AHE=∠CHD,∴∠EAH=∠ECB.
在△EAH和△ECB中,
∠EAH=∠BCE,
∠AEH=∠CEB,
EH=EB,
课堂训练
7.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E ,AD,CE交于点H,已知EH=EB=3,AE=4,求CH的长.
∴△EAH≌△ECB(AAS).
∴AE=CE,则CE=4.
∴CH=CE-EH=4-3=1.
“HL”是直角三角形独有的判定方法,但直角三角形的判定方法很多,判定时,应抓住“直角”这个隐含条件,选择合适的方法求证.
课堂训练
8.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P,Q两点同时出发,运动多少分钟后,△CAP与△PQB全等?
解:CA⊥AB于点A, DB⊥AB于点B ,
∴∠A=∠B=90°.
设运动x分钟后,△CAP与△PQB全等,则BP=xm , BQ=2xm,AP=(12-x)m.分两种情况:
①若BP=AC ,则x=4,∴AP=12-4=8(m) , BQ=8m, ∴AP=BQ ,此时,△CAP≌△PBQ(SAS);
课堂训练
8.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P,Q两点同时出发,运动多少分钟后,△CAP与△PQB全等?
②若BP=AP ,则12-x=x,解得x=6 , 则BQ=12m≠AC,
此时,△CAP与△PBQ不全等.
综上所示,运动4分钟后,△CAP与△PQB全等.
判定三角形全等的关键是找对应边和对应角,由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.
