初中数学人教版八上13.1.1轴对称 同步课件(共39张PPT)
文档属性
| 名称 | 初中数学人教版八上13.1.1轴对称 同步课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 21:59:30 | ||
图片预览









文档简介
(共39张PPT)
第十三章 轴对称
13.1 轴对称
13.1.1 轴对称
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.通过观察实例,初步了解轴对称图形和两个图形成轴对称
的概念.(重点)
2.能够识别简单的轴对称图形及其对称轴.(重点)
3.理解轴对称图形和两个图形成轴对称这两个概念的区别与联系,探索轴对称现象共同特征.(重点、难点)
新课导入
情境引入
观察下列图形,说一说它们有什么共同的特点?
新课导入
情境引入
新知探究
将准备好的手工纸对折,剪出一个图案(折痕处不要完全剪断),再打开这张对折的纸,你得到了什么,它有什么特点?
知识点1 轴对称图形
示例
新知探究
知识点1 轴对称图形
新知探究
知识点1 轴对称图形
像窗花一样,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.这时,我们也说这个图形关于这条直线(成轴)对称.
新知探究
知识点1 轴对称图形
根据以上定义,你能举出生活中见过的一些轴对称图形的例子吗?
新知探究
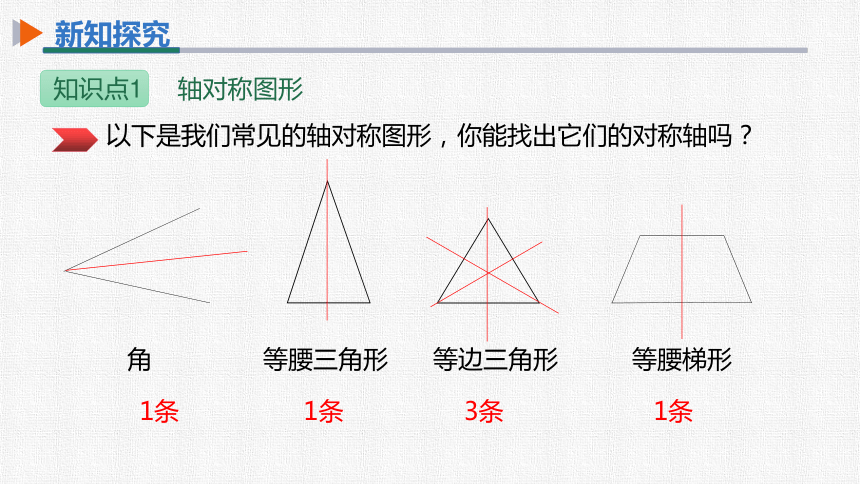
知识点1 轴对称图形
以下是我们常见的轴对称图形,你能找出它们的对称轴吗?
1条
1条
3条
1条
角 等腰三角形 等边三角形 等腰梯形
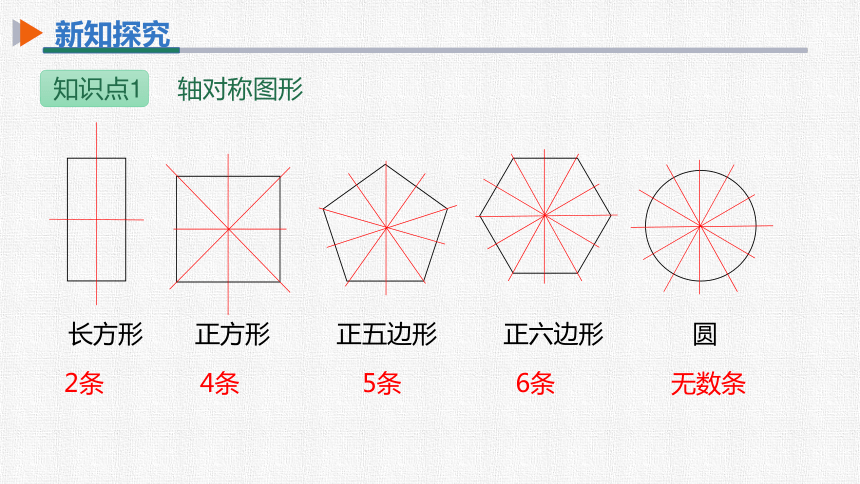
新知探究
知识点1 轴对称图形
2条
4条
5条
6条
无数条
长方形 正方形 正五边形 正六边形 圆
新知探究
知识点1 轴对称图形
(1)轴对称图形是对一个图形来讲的,它是一个图形自身的对称特征,它被对称轴分成的两部分能够互相重合.
(2)一个轴对称图形的对称轴可以有一条,也可以有多条,甚至无数条.
新知探究
下列图形中,是轴对称图形且对称轴条数最多的是
( )
A. B. C. D.
【解析】A.是轴对称图形,共有1条对称轴;B.不是轴对称图形,没有对称轴;C.不是轴对称图形,没有对称轴;D.是轴对称图形,共有2条对称轴.故选D.
D
跟踪训练
新知探究
将准备好的手工纸对折,并用小刀在纸的中央随意刻出一个图案,将纸打开后铺平,你得到了几个图形,它(们)有什么特点?
知识点2 两个图形成轴对称
示例
新知探究
知识点2 两个图形成轴对称
图中的每一对图形沿着虚线折叠,左边的图形能与右边的图形重合.
新知探究
知识点2 两个图形成轴对称
对称轴
像这样,把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后能够重合的点是对应点,叫做对称点.
B
A
C
A′
C′
请标出该图中点A,B,C的对称点A′,B′,C′.
B′
新知探究
理解两个图形成轴对称定义的三点:
1.有两个图形;
2.存在一条直线;
3.使得一个图形沿着这条直线折叠后与另外一个图形重合.
知识点2 两个图形成轴对称
新知探究
轴对称图形
两个图形成轴对称
仔细观察,下列两个图形有什么区别?
知识点2 两个图形成轴对称
新知探究
轴对称图形
把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴对称.
知识点2 两个图形成轴对称
新知探究
两个图形成轴对称
把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.
知识点2 两个图形成轴对称
新知探究
轴对称图形 两个图形成轴对称
区别
联系
一个图形
两个图形
一个图形被直线分成两部分
两个图形分别位于一条直线两旁
对称点在这个图形上
对称点分别在这两个图形上
对称轴有一条或多条或无数条
对称轴只有一条
1.都能沿着某条直线折叠后相互重合;
2.把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.把一个轴对称图形沿着对称轴分成两个图形,这两个图形关于这条轴对称.
知识点2 两个图形成轴对称
新知探究
知识点2 两个图形成轴对称
成轴对称的两个图形全等.如果把一个轴对称图形沿对称轴分成两个图形,这两个图形全等,并且也是成轴对称的.
思考 成轴对称的两个图形全等吗? 如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?这两个图形对称吗?
注意:但是全等的两个图形不一定成轴对称.
新知探究
全等,且成轴对称
E
E
E
E
知识点2 两个图形成轴对称
全等,但不成轴对称
新知探究
跟踪训练
下列三组图片中有哪几组图形成轴对称?是的请指出它的对称点.
A
B
C
D
A1
B1
C1
D1
A
B
C
D
A
B
C
D
A1
B1
C1
D1
不是
是
是
新知探究
知识点3 轴对称和轴对称图形的性质
解:∵△ABC和△A'B'C'关于直线MN对称,
∴将△ABC沿着MN折叠后,能和△A'B'C'完全重合.
∵点A和点A'是对称点.∴点A与点A'重合.
C'
B
B'
A'
M
N
A
C
思考 如图,△ABC和△A'B'C'关于直线MN对称,点A',B',C'分别是点A,B,C的对称点,线段AA',BB',CC'与直线MN有什么关系?
新知探究
知识点4 轴对称和轴对称图形的性质
C'
B
B'
A'
M
N
A
C
设AA'交对称轴MN于点P,E,F,
则有AP=A'P,∠MPA=∠MPA'=90°.
同理可得BE=B'E,∠MEB=∠MEB'=90°;
CF=C'F',∠MFC=∠MFC'=90°.
因此,对称轴经过对称点所连线段的中点,并且垂直于这条线段.
P
E
F
新知探究
知识点3 轴对称和轴对称图形的性质
如图,若 AO=BO,l⊥AB,
则直线l是线段AB的垂直平分线.
线段垂直平分线的定义:
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
A
B
l
O
┐
如图,若直线l是线段AB的垂直平分线,
则AO=BO,l⊥AB.
新知探究
知识点3 轴对称和轴对称图形的性质
C'
B
B'
A'
M
N
A
C
如图,△ABC和△A'B'C'关于直线MN对称,则直线MN是线段AA',BB',CC'的垂直平分线.
图形轴对称的性质:
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
新知探究
知识点3 轴对称和轴对称图形的性质
如图,l垂直平分AA',l垂直平分BB'.
A
B
A'
B'
l
轴对称图形的性质:
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
新知探究
如图,如果直线l是△ABC的对称轴,其中∠C=66°,那么∠BAC的度数为( )
A.66° B. 48° C.58° D.24°
【解析】根据轴对称的性质知,∠B=
∠C=66°.根据三角形内角和定理知,∠BAC=180°-∠B-∠C=48°.故选B.
B
跟踪训练
课堂小结
轴对称
轴对称图形
两个图形成轴对称
轴对称图形与两个图形成轴对称
定义
性质
定义
性质
区别
联系
课堂训练
1. “国士无双”是人民对“杂交水稻之父”袁隆平院士的赞誉.下列四个汉字中是轴对称图形的是( )
B
A. B. C. D.
C
2. 将一张矩形的纸对折,然后用笔尖在上面扎出
“B”,再把它铺平,你可见到( )
A. B. C. D.
课堂训练
3.如图,△ABC和△DEF关于直线MN对称,则以下结论中错误的是( )
A.AB//DF B.∠B=∠E
C.AB=DE D.AD的连线被直线MN垂直平分
A
课堂训练
4. 如图,在Rt△ACB中,∠BAC=90°,AD⊥BC,垂足为D,△ABD与△ADB'关于直线AD对称,点B的对称点是点B',若∠B'AC=14° ,则∠B的度数为( )
A.38° B. 48° C.50° D.52°
【解析】∵∠BAC=90°,∠BAD+∠B'AD+
∠B'AC=90°.∵△ABD与△ADB'关于直线AD对称,
∴∠BAD=∠B'AD,则2∠BAD+∠B'AC=90°,即2∠BAD+14°=90°.
解得∠BAD=38°.∵AD⊥BC,∴∠B=90°-38°=52°.故选D.
D
课堂训练
5.判断下列说法的对错:
(1)轴对称图形必有对称轴.( )
(2)轴对称图形至少有一条对称轴.( )
(3)关于某直线成轴对称的两个图形必能互相重合.( )
(4)两个完全互相重合的图形必是轴对称.( )
(5)成轴对称的两个图形是全等形.( )
(6)线段的对称轴是经过线段中点且垂直于线段的射线( )
(7)成轴对称的两个图形的对应角相等,对应边相等.( )
√
√
√
×
√
×
√
课堂训练
6.如图,小明从镜子中看到电子钟显示的时间是20 : 51 ,那么实际时间为 .
12:05
课堂训练
7.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 .
【解析】根据正方形的轴对称性得,阴影部分的面积等于正方形ABCD面积的一半,∵正方形ABCD的边长为4cm,∴S阴影=42÷2=8(cm2).
8cm2
课堂训练
8.找出下面每个轴对称图形的对称轴.
课堂训练
9.如图,在3×3的正方形网格中,有两个小正方形已被涂上阴影,请再将图中剩余小正方形中任意一个涂上阴影,使整个图案构成一个轴对称图形,你有几种涂法?
课堂训练
解:共有5种.
第十三章 轴对称
13.1 轴对称
13.1.1 轴对称
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.通过观察实例,初步了解轴对称图形和两个图形成轴对称
的概念.(重点)
2.能够识别简单的轴对称图形及其对称轴.(重点)
3.理解轴对称图形和两个图形成轴对称这两个概念的区别与联系,探索轴对称现象共同特征.(重点、难点)
新课导入
情境引入
观察下列图形,说一说它们有什么共同的特点?
新课导入
情境引入
新知探究
将准备好的手工纸对折,剪出一个图案(折痕处不要完全剪断),再打开这张对折的纸,你得到了什么,它有什么特点?
知识点1 轴对称图形
示例
新知探究
知识点1 轴对称图形
新知探究
知识点1 轴对称图形
像窗花一样,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.这时,我们也说这个图形关于这条直线(成轴)对称.
新知探究
知识点1 轴对称图形
根据以上定义,你能举出生活中见过的一些轴对称图形的例子吗?
新知探究
知识点1 轴对称图形
以下是我们常见的轴对称图形,你能找出它们的对称轴吗?
1条
1条
3条
1条
角 等腰三角形 等边三角形 等腰梯形
新知探究
知识点1 轴对称图形
2条
4条
5条
6条
无数条
长方形 正方形 正五边形 正六边形 圆
新知探究
知识点1 轴对称图形
(1)轴对称图形是对一个图形来讲的,它是一个图形自身的对称特征,它被对称轴分成的两部分能够互相重合.
(2)一个轴对称图形的对称轴可以有一条,也可以有多条,甚至无数条.
新知探究
下列图形中,是轴对称图形且对称轴条数最多的是
( )
A. B. C. D.
【解析】A.是轴对称图形,共有1条对称轴;B.不是轴对称图形,没有对称轴;C.不是轴对称图形,没有对称轴;D.是轴对称图形,共有2条对称轴.故选D.
D
跟踪训练
新知探究
将准备好的手工纸对折,并用小刀在纸的中央随意刻出一个图案,将纸打开后铺平,你得到了几个图形,它(们)有什么特点?
知识点2 两个图形成轴对称
示例
新知探究
知识点2 两个图形成轴对称
图中的每一对图形沿着虚线折叠,左边的图形能与右边的图形重合.
新知探究
知识点2 两个图形成轴对称
对称轴
像这样,把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后能够重合的点是对应点,叫做对称点.
B
A
C
A′
C′
请标出该图中点A,B,C的对称点A′,B′,C′.
B′
新知探究
理解两个图形成轴对称定义的三点:
1.有两个图形;
2.存在一条直线;
3.使得一个图形沿着这条直线折叠后与另外一个图形重合.
知识点2 两个图形成轴对称
新知探究
轴对称图形
两个图形成轴对称
仔细观察,下列两个图形有什么区别?
知识点2 两个图形成轴对称
新知探究
轴对称图形
把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴对称.
知识点2 两个图形成轴对称
新知探究
两个图形成轴对称
把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.
知识点2 两个图形成轴对称
新知探究
轴对称图形 两个图形成轴对称
区别
联系
一个图形
两个图形
一个图形被直线分成两部分
两个图形分别位于一条直线两旁
对称点在这个图形上
对称点分别在这两个图形上
对称轴有一条或多条或无数条
对称轴只有一条
1.都能沿着某条直线折叠后相互重合;
2.把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.把一个轴对称图形沿着对称轴分成两个图形,这两个图形关于这条轴对称.
知识点2 两个图形成轴对称
新知探究
知识点2 两个图形成轴对称
成轴对称的两个图形全等.如果把一个轴对称图形沿对称轴分成两个图形,这两个图形全等,并且也是成轴对称的.
思考 成轴对称的两个图形全等吗? 如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?这两个图形对称吗?
注意:但是全等的两个图形不一定成轴对称.
新知探究
全等,且成轴对称
E
E
E
E
知识点2 两个图形成轴对称
全等,但不成轴对称
新知探究
跟踪训练
下列三组图片中有哪几组图形成轴对称?是的请指出它的对称点.
A
B
C
D
A1
B1
C1
D1
A
B
C
D
A
B
C
D
A1
B1
C1
D1
不是
是
是
新知探究
知识点3 轴对称和轴对称图形的性质
解:∵△ABC和△A'B'C'关于直线MN对称,
∴将△ABC沿着MN折叠后,能和△A'B'C'完全重合.
∵点A和点A'是对称点.∴点A与点A'重合.
C'
B
B'
A'
M
N
A
C
思考 如图,△ABC和△A'B'C'关于直线MN对称,点A',B',C'分别是点A,B,C的对称点,线段AA',BB',CC'与直线MN有什么关系?
新知探究
知识点4 轴对称和轴对称图形的性质
C'
B
B'
A'
M
N
A
C
设AA'交对称轴MN于点P,E,F,
则有AP=A'P,∠MPA=∠MPA'=90°.
同理可得BE=B'E,∠MEB=∠MEB'=90°;
CF=C'F',∠MFC=∠MFC'=90°.
因此,对称轴经过对称点所连线段的中点,并且垂直于这条线段.
P
E
F
新知探究
知识点3 轴对称和轴对称图形的性质
如图,若 AO=BO,l⊥AB,
则直线l是线段AB的垂直平分线.
线段垂直平分线的定义:
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
A
B
l
O
┐
如图,若直线l是线段AB的垂直平分线,
则AO=BO,l⊥AB.
新知探究
知识点3 轴对称和轴对称图形的性质
C'
B
B'
A'
M
N
A
C
如图,△ABC和△A'B'C'关于直线MN对称,则直线MN是线段AA',BB',CC'的垂直平分线.
图形轴对称的性质:
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
新知探究
知识点3 轴对称和轴对称图形的性质
如图,l垂直平分AA',l垂直平分BB'.
A
B
A'
B'
l
轴对称图形的性质:
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
新知探究
如图,如果直线l是△ABC的对称轴,其中∠C=66°,那么∠BAC的度数为( )
A.66° B. 48° C.58° D.24°
【解析】根据轴对称的性质知,∠B=
∠C=66°.根据三角形内角和定理知,∠BAC=180°-∠B-∠C=48°.故选B.
B
跟踪训练
课堂小结
轴对称
轴对称图形
两个图形成轴对称
轴对称图形与两个图形成轴对称
定义
性质
定义
性质
区别
联系
课堂训练
1. “国士无双”是人民对“杂交水稻之父”袁隆平院士的赞誉.下列四个汉字中是轴对称图形的是( )
B
A. B. C. D.
C
2. 将一张矩形的纸对折,然后用笔尖在上面扎出
“B”,再把它铺平,你可见到( )
A. B. C. D.
课堂训练
3.如图,△ABC和△DEF关于直线MN对称,则以下结论中错误的是( )
A.AB//DF B.∠B=∠E
C.AB=DE D.AD的连线被直线MN垂直平分
A
课堂训练
4. 如图,在Rt△ACB中,∠BAC=90°,AD⊥BC,垂足为D,△ABD与△ADB'关于直线AD对称,点B的对称点是点B',若∠B'AC=14° ,则∠B的度数为( )
A.38° B. 48° C.50° D.52°
【解析】∵∠BAC=90°,∠BAD+∠B'AD+
∠B'AC=90°.∵△ABD与△ADB'关于直线AD对称,
∴∠BAD=∠B'AD,则2∠BAD+∠B'AC=90°,即2∠BAD+14°=90°.
解得∠BAD=38°.∵AD⊥BC,∴∠B=90°-38°=52°.故选D.
D
课堂训练
5.判断下列说法的对错:
(1)轴对称图形必有对称轴.( )
(2)轴对称图形至少有一条对称轴.( )
(3)关于某直线成轴对称的两个图形必能互相重合.( )
(4)两个完全互相重合的图形必是轴对称.( )
(5)成轴对称的两个图形是全等形.( )
(6)线段的对称轴是经过线段中点且垂直于线段的射线( )
(7)成轴对称的两个图形的对应角相等,对应边相等.( )
√
√
√
×
√
×
√
课堂训练
6.如图,小明从镜子中看到电子钟显示的时间是20 : 51 ,那么实际时间为 .
12:05
课堂训练
7.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 .
【解析】根据正方形的轴对称性得,阴影部分的面积等于正方形ABCD面积的一半,∵正方形ABCD的边长为4cm,∴S阴影=42÷2=8(cm2).
8cm2
课堂训练
8.找出下面每个轴对称图形的对称轴.
课堂训练
9.如图,在3×3的正方形网格中,有两个小正方形已被涂上阴影,请再将图中剩余小正方形中任意一个涂上阴影,使整个图案构成一个轴对称图形,你有几种涂法?
课堂训练
解:共有5种.
