初中数学人教版八上 13.3.2第2课时含30°角的直角三角形的性质 同步课件(28张PPT)
文档属性
| 名称 | 初中数学人教版八上 13.3.2第2课时含30°角的直角三角形的性质 同步课件(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 22:11:33 | ||
图片预览








文档简介
(共28张PPT)
第十三章 轴对称
13.3 等腰三角形
13.3.2 等边三角形
第2课时 含30°角的直角三角形的性质
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.掌握含有30°角的直角三角形的性质.(重点)
2.经历探索含有30°角的直角三角形性质的过程,并运用其进行有关的证明和计算.(难点)
新课导入
复习引入
图形 等腰三角形 等边三角形
性质 边
角
三线合一
对称性
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
3条对称轴
1条对称轴
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60
两条边相等
三条边都相等
新课导入
复习引入
图形 等腰三角形 等边三角形
判定 边(定义)
角
特殊法
三个角都相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形.
两个角相等的三角形是等腰三角形
两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
新知探究
动手操作 用直尺量一量含有30°角的直角三角板的最短直角边(也即是30°角所对的直角边)与斜边的长度,你有什么发现吗?
知识点 含30°角的直角三角形的性质
最短的直角边长 斜边长
学生甲
学生乙
学生丙
6.7cm
13.5cm
6.8cm
13.5cm
14.4cm
29cm
×2≈
×2≈
×2≈
新知探究
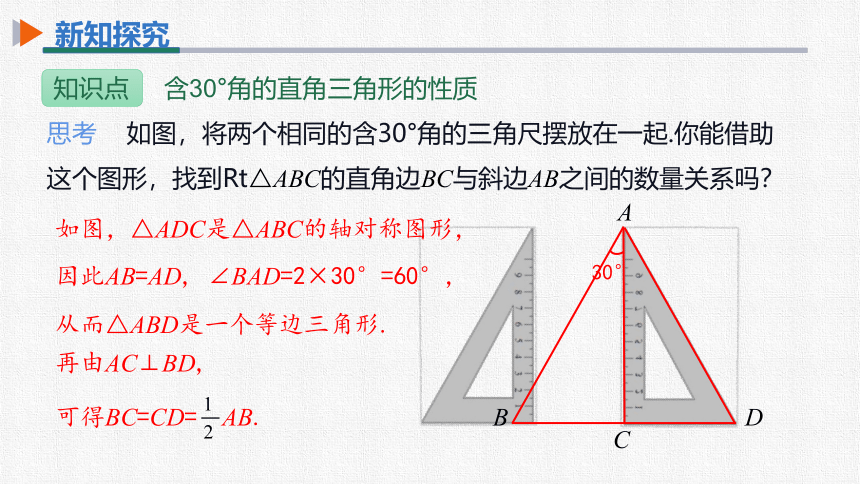
思考 如图,将两个相同的含30°角的三角尺摆放在一起.你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
知识点 含30°角的直角三角形的性质
A
B
D
C
30°
如图,△ADC是△ABC的轴对称图形,
因此AB=AD, ∠BAD=2×30°=60°,
从而△ABD是一个等边三角形.
再由AC⊥BD,
可得BC=CD= AB.
新知探究
猜想:30°角所对的直角边的长度是斜边长度的一半.
你能证明这个猜想的正确性吗?
知识点 含30°角的直角三角形的性质
新知探究
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
求证:BC= AB.
证明:在△ABC中,
∵∠C=90°,∠A=30°, ∴∠B=60°.
A
B
C
∴BC= AB.
∴BC = BD.
证法一:
如图,延长BC到点D,使BD=AB,连接AD,
则△ABD是等边三角形.
又∵AC⊥BD,
D
知识点 含30°角的直角三角形的性质
新知探究
证明:在BA上截取BE=BC,连接EC.
A
B
C
即BC= AB.
证法二:
E
∵∠B= 60°,BE=BC.∴△BCE是等边三角形,
∴∠BEC= 60°,BE=EC.
∵∠A= 30°,
∴∠ECA=∠BEC-∠A=60°-30° = 30°.
∴AE=EC,∴AE=BE=BC,
∴AB=AE+BE=2BC,
知识点 含30°角的直角三角形的性质
新知探究
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
该性质的几何语言:
在Rt△ABC 中,
∵∠C=90°,∠A=30°,
∴BC= AB.
A
B
C
该性质是“含有30°角的直角三角形”所特有的,一般的直角三角形没有这个性质.
知识点 含30°角的直角三角形的性质
新知探究
例1 如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC,DE要多长?
A
B
C
D
E
解:∵DE⊥AC,BC ⊥AC,∠A=30 °,
∴BC= AB,DE= AD.
∴BC= ×7.4=3.7(m).
又AD= AB,
∴DE= AD= ×3.7=1.85(m).
答:立柱BC的长是3.7m,DE的长是1.85m.
知识点 含30°角的直角三角形的性质
新知探究
例2 如图,在Rt△ABC中,CD是斜边AB上的高,∠B=30°.
(1)若CD=8cm,则BC的长度是多少?
解:(1)∵CD是斜边AB边上的高,
∴∠BDC=90°.
∵在Rt△BCD中,∠B=30°,CD=8cm,
∴BC=2CD=16cm.
B
C
A
└
D
知识点 含30°角的直角三角形的性质
新知探究
例2 如图,在Rt△ABC中,CD是斜边AB上的高,∠B=30°.
(2)若AD=3cm,则AB的长度是多少?
解:(2)在Rt△ABC中,∵∠B=30°,∴∠A=60°,∵CD是斜边AB边上的高,∴∠ADC=90°.∴∠ACD=30°.
∵在Rt△ACD中,∠ACD=30°,AD=3cm,
∴AC=2AD=6cm.∵在Rt△ABC中,∠B=30°,AC=6cm,
∴AB=2AC=12cm.
B
C
A
└
D
知识点 含30°角的直角三角形的性质
新知探究
注意:运用含30°角的直角三角形的性质求线段长时,要分清线段所在的直角三角形.
知识点 含30°角的直角三角形的性质
新知探究
例3 如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AE=6cm,则AC=( )
A.6cm B.5cm C.4cm D.3cm
D
【解析】DE垂直平分AB AE=BE
∠B=∠BAE=15°
外角性质
∠AEC=30°从而得到AC的长.
知识点 含30°角的直角三角形的性质
新知探究
含30°角的直角三角形的性质是求线段长度和证明线段之间倍分关系的重要工具,解题时,一般先是寻找30°角所在的直角三角形,得到斜边与直角边的关系,当30°角不在一个直角三角形中时,可考虑作辅助线构造含30°角的直角三角形,如:作垂线得到含30°角的直角三角形,或作等腰三角形构造顶角的邻补角为60°.当三角形中含有15°,30°,60°,120°角时,也可通过添加辅助线,构造含30°角的直角三角形求解.
知识点 含30°角的直角三角形的性质
新知探究
常见的模型有如下几种(图中所标的红色的角均为30°):
15°
15°
60°
60°
60°
120°
120°
知识点 含30°角的直角三角形的性质
课堂小结
含30°角的直角三角形的性质
内容
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
注意事项
1.在直角三角形中,且该直角三角形中有一内角为30°
2.分清所求线段在哪个直角三角形中
课堂训练
1.如图,在△ABC中, AD是边BC的垂直平分线,∠B=60°,BD=2 ,那么AC的长度是( )
A.1 B.2 C.3 D.4
D
课堂训练
2.如图,在△ABC中,∠C=60°, AD是BC边上的高,点E为AD的中点,连接BE并延长交AC于点F .若∠AFB=90°, EF=2,则BF长为( )
A.4 B.6 C.8 D.10
D
课堂训练
3.如图,在等边△ABC中, D是AB的中点,DE⊥AC于点E,EF⊥BC于点F ,已知AB=8,则BF的长为( )
A.3 B.4 C.5 D.6
C
课堂训练
4.如图,∠AOP=∠BOP=15°,PC∥OA交OB于点C,PD⊥OA于点D,若PC=3,则PD等于( )
A.3 B.2
C.1.5 D.1
E
C
【解析】如图,过点P作PE⊥OB于点E.∵PC∥OA,∴∠AOP=∠CPO=15°,∴∠PCE=∠BOP+∠CPO=15°+15°=30°.又∵PC=3,∴PE=1.5.∵∠AOP=∠BOP,PD⊥OA,∴PD=PE=1.5.故选C.
课堂训练
6.如图,在△ABC中,AB=BC ,∠ABC=120°,过点B作BD⊥BC,交AC于点D,若AD=1 ,则CD的长度为 .
2
5.在△ABC中,∠A: ∠B: ∠C=1:2:3,若AB=10,则BC= .
5
课堂训练
证明:∵AB=AC,∠BAC=120°, ∴∠B=∠C=30°.
∵D是BC的中点,∴AD⊥BC.
∴∠ADC=90°,∠BAD=∠DAC=60°.
∴AB=2AD.∵DE⊥AB,∴∠AED=90°,
∴∠ADE=30°,∴AD=2AE.
∴AB=4AE,∴BE=3AE.
7.在△ABC中,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AB于点E,求证:BE=3EA.
8.求证:有一个锐角是30°的直角三角形斜边上的高把斜边分成1:3的两条线段.
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°, CD⊥AB.
求证:BD:AD=1:3.
B
C
A
└
D
课堂训练
证明:在Rt△ABC中,∠C=90°,∠A=30°,
∴AB=2BC , ∠B=90-30°=60° ,
∵CD⊥AB ,∴∠CDB=90° ,
∴∠BCD=30° ,∴BC=2BD .
∴AB=4BD,∴BD:AD=1:3.
故有一个锐角是30°的直角三角形斜边上的高把斜边分成1:3的两条线段.
B
C
A
└
D
课堂训练
9.如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN//BC交AC于点N,且MN平分∠AMC,若AN=1,求BC的长.
解:∵CM平分∠ACB,MN平分∠AMC,
∴∠NCM=∠BCM,∠AMN=∠NMC.
∵MN//BC,∴∠AMN=∠B,∠NMC=∠BCM.
∴∠AMN=∠B=∠NMC=∠BCM=∠NCM. ∴NM=NC.
∵∠ACB=∠NCM+∠BCM,∴∠ACB=2∠B.
课堂训练
A
B
C
M
N
└
9.如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN//BC交AC于点N,且MN平分∠AMC,若AN=1,求BC的长.
∵∠A=90°,∴∠ACB+∠B=90°,∴∠B=30°.∴∠AMN=∠B=30°.
∵∠A=90°,∠AMN=30°,AN=1,∴MN=2.
∵AC=AN+NC=AN+MN=3,∴BC=2AC=6.
课堂训练
A
B
C
M
N
└
第十三章 轴对称
13.3 等腰三角形
13.3.2 等边三角形
第2课时 含30°角的直角三角形的性质
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.掌握含有30°角的直角三角形的性质.(重点)
2.经历探索含有30°角的直角三角形性质的过程,并运用其进行有关的证明和计算.(难点)
新课导入
复习引入
图形 等腰三角形 等边三角形
性质 边
角
三线合一
对称性
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
3条对称轴
1条对称轴
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60
两条边相等
三条边都相等
新课导入
复习引入
图形 等腰三角形 等边三角形
判定 边(定义)
角
特殊法
三个角都相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形.
两个角相等的三角形是等腰三角形
两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
新知探究
动手操作 用直尺量一量含有30°角的直角三角板的最短直角边(也即是30°角所对的直角边)与斜边的长度,你有什么发现吗?
知识点 含30°角的直角三角形的性质
最短的直角边长 斜边长
学生甲
学生乙
学生丙
6.7cm
13.5cm
6.8cm
13.5cm
14.4cm
29cm
×2≈
×2≈
×2≈
新知探究
思考 如图,将两个相同的含30°角的三角尺摆放在一起.你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
知识点 含30°角的直角三角形的性质
A
B
D
C
30°
如图,△ADC是△ABC的轴对称图形,
因此AB=AD, ∠BAD=2×30°=60°,
从而△ABD是一个等边三角形.
再由AC⊥BD,
可得BC=CD= AB.
新知探究
猜想:30°角所对的直角边的长度是斜边长度的一半.
你能证明这个猜想的正确性吗?
知识点 含30°角的直角三角形的性质
新知探究
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
求证:BC= AB.
证明:在△ABC中,
∵∠C=90°,∠A=30°, ∴∠B=60°.
A
B
C
∴BC= AB.
∴BC = BD.
证法一:
如图,延长BC到点D,使BD=AB,连接AD,
则△ABD是等边三角形.
又∵AC⊥BD,
D
知识点 含30°角的直角三角形的性质
新知探究
证明:在BA上截取BE=BC,连接EC.
A
B
C
即BC= AB.
证法二:
E
∵∠B= 60°,BE=BC.∴△BCE是等边三角形,
∴∠BEC= 60°,BE=EC.
∵∠A= 30°,
∴∠ECA=∠BEC-∠A=60°-30° = 30°.
∴AE=EC,∴AE=BE=BC,
∴AB=AE+BE=2BC,
知识点 含30°角的直角三角形的性质
新知探究
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
该性质的几何语言:
在Rt△ABC 中,
∵∠C=90°,∠A=30°,
∴BC= AB.
A
B
C
该性质是“含有30°角的直角三角形”所特有的,一般的直角三角形没有这个性质.
知识点 含30°角的直角三角形的性质
新知探究
例1 如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC,DE要多长?
A
B
C
D
E
解:∵DE⊥AC,BC ⊥AC,∠A=30 °,
∴BC= AB,DE= AD.
∴BC= ×7.4=3.7(m).
又AD= AB,
∴DE= AD= ×3.7=1.85(m).
答:立柱BC的长是3.7m,DE的长是1.85m.
知识点 含30°角的直角三角形的性质
新知探究
例2 如图,在Rt△ABC中,CD是斜边AB上的高,∠B=30°.
(1)若CD=8cm,则BC的长度是多少?
解:(1)∵CD是斜边AB边上的高,
∴∠BDC=90°.
∵在Rt△BCD中,∠B=30°,CD=8cm,
∴BC=2CD=16cm.
B
C
A
└
D
知识点 含30°角的直角三角形的性质
新知探究
例2 如图,在Rt△ABC中,CD是斜边AB上的高,∠B=30°.
(2)若AD=3cm,则AB的长度是多少?
解:(2)在Rt△ABC中,∵∠B=30°,∴∠A=60°,∵CD是斜边AB边上的高,∴∠ADC=90°.∴∠ACD=30°.
∵在Rt△ACD中,∠ACD=30°,AD=3cm,
∴AC=2AD=6cm.∵在Rt△ABC中,∠B=30°,AC=6cm,
∴AB=2AC=12cm.
B
C
A
└
D
知识点 含30°角的直角三角形的性质
新知探究
注意:运用含30°角的直角三角形的性质求线段长时,要分清线段所在的直角三角形.
知识点 含30°角的直角三角形的性质
新知探究
例3 如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AE=6cm,则AC=( )
A.6cm B.5cm C.4cm D.3cm
D
【解析】DE垂直平分AB AE=BE
∠B=∠BAE=15°
外角性质
∠AEC=30°从而得到AC的长.
知识点 含30°角的直角三角形的性质
新知探究
含30°角的直角三角形的性质是求线段长度和证明线段之间倍分关系的重要工具,解题时,一般先是寻找30°角所在的直角三角形,得到斜边与直角边的关系,当30°角不在一个直角三角形中时,可考虑作辅助线构造含30°角的直角三角形,如:作垂线得到含30°角的直角三角形,或作等腰三角形构造顶角的邻补角为60°.当三角形中含有15°,30°,60°,120°角时,也可通过添加辅助线,构造含30°角的直角三角形求解.
知识点 含30°角的直角三角形的性质
新知探究
常见的模型有如下几种(图中所标的红色的角均为30°):
15°
15°
60°
60°
60°
120°
120°
知识点 含30°角的直角三角形的性质
课堂小结
含30°角的直角三角形的性质
内容
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
注意事项
1.在直角三角形中,且该直角三角形中有一内角为30°
2.分清所求线段在哪个直角三角形中
课堂训练
1.如图,在△ABC中, AD是边BC的垂直平分线,∠B=60°,BD=2 ,那么AC的长度是( )
A.1 B.2 C.3 D.4
D
课堂训练
2.如图,在△ABC中,∠C=60°, AD是BC边上的高,点E为AD的中点,连接BE并延长交AC于点F .若∠AFB=90°, EF=2,则BF长为( )
A.4 B.6 C.8 D.10
D
课堂训练
3.如图,在等边△ABC中, D是AB的中点,DE⊥AC于点E,EF⊥BC于点F ,已知AB=8,则BF的长为( )
A.3 B.4 C.5 D.6
C
课堂训练
4.如图,∠AOP=∠BOP=15°,PC∥OA交OB于点C,PD⊥OA于点D,若PC=3,则PD等于( )
A.3 B.2
C.1.5 D.1
E
C
【解析】如图,过点P作PE⊥OB于点E.∵PC∥OA,∴∠AOP=∠CPO=15°,∴∠PCE=∠BOP+∠CPO=15°+15°=30°.又∵PC=3,∴PE=1.5.∵∠AOP=∠BOP,PD⊥OA,∴PD=PE=1.5.故选C.
课堂训练
6.如图,在△ABC中,AB=BC ,∠ABC=120°,过点B作BD⊥BC,交AC于点D,若AD=1 ,则CD的长度为 .
2
5.在△ABC中,∠A: ∠B: ∠C=1:2:3,若AB=10,则BC= .
5
课堂训练
证明:∵AB=AC,∠BAC=120°, ∴∠B=∠C=30°.
∵D是BC的中点,∴AD⊥BC.
∴∠ADC=90°,∠BAD=∠DAC=60°.
∴AB=2AD.∵DE⊥AB,∴∠AED=90°,
∴∠ADE=30°,∴AD=2AE.
∴AB=4AE,∴BE=3AE.
7.在△ABC中,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AB于点E,求证:BE=3EA.
8.求证:有一个锐角是30°的直角三角形斜边上的高把斜边分成1:3的两条线段.
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°, CD⊥AB.
求证:BD:AD=1:3.
B
C
A
└
D
课堂训练
证明:在Rt△ABC中,∠C=90°,∠A=30°,
∴AB=2BC , ∠B=90-30°=60° ,
∵CD⊥AB ,∴∠CDB=90° ,
∴∠BCD=30° ,∴BC=2BD .
∴AB=4BD,∴BD:AD=1:3.
故有一个锐角是30°的直角三角形斜边上的高把斜边分成1:3的两条线段.
B
C
A
└
D
课堂训练
9.如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN//BC交AC于点N,且MN平分∠AMC,若AN=1,求BC的长.
解:∵CM平分∠ACB,MN平分∠AMC,
∴∠NCM=∠BCM,∠AMN=∠NMC.
∵MN//BC,∴∠AMN=∠B,∠NMC=∠BCM.
∴∠AMN=∠B=∠NMC=∠BCM=∠NCM. ∴NM=NC.
∵∠ACB=∠NCM+∠BCM,∴∠ACB=2∠B.
课堂训练
A
B
C
M
N
└
9.如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN//BC交AC于点N,且MN平分∠AMC,若AN=1,求BC的长.
∵∠A=90°,∴∠ACB+∠B=90°,∴∠B=30°.∴∠AMN=∠B=30°.
∵∠A=90°,∠AMN=30°,AN=1,∴MN=2.
∵AC=AN+NC=AN+MN=3,∴BC=2AC=6.
课堂训练
A
B
C
M
N
└
