初中数学人教版八上 14.1.1同底数幂的乘法 同步课件(27张PPT)
文档属性
| 名称 | 初中数学人教版八上 14.1.1同底数幂的乘法 同步课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 976.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 22:12:37 | ||
图片预览








文档简介
(共27张PPT)
第十四章 整式的乘法与因式分解
14.1 整式的乘法
14.1.1 同底数幂的乘法
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.理解并掌握同底数幂的乘法法则.(重点)
2.能够运用同底数幂的乘法法则进行相关计算.(难点)
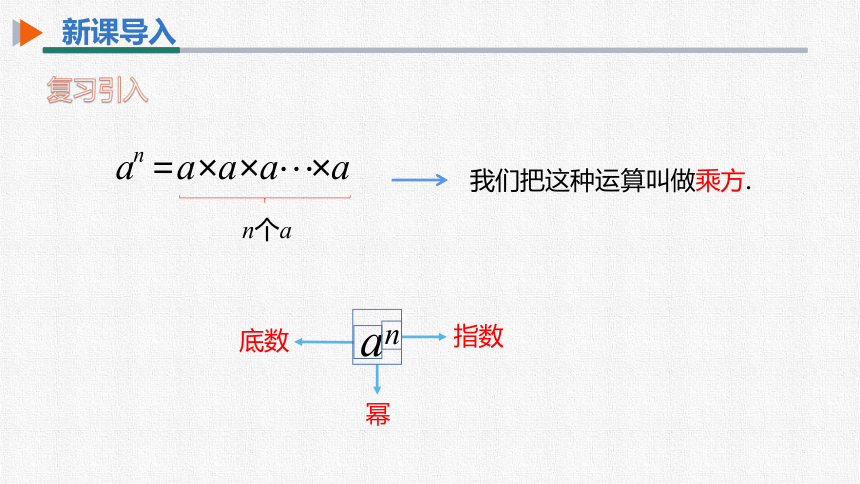
新课导入
复习引入
我们把这种运算叫做乘方.
n个a
an
底数
幂
指数
新课导入
复习引入
请按照乘方的定义填空.
(1)54 =( ) ;
(2)12×12×12×12×12×12=( ) ;
(3) (-3)10的底数是 ,指数是 ;
(4)(b-a)2的底数是 ,指数是 .
5×5×5×5
10
2
-3
(b-a)
126
练一练
新知探究
知识点 同底数幂的乘法
问题 一种电子计算机每秒可进行1千万亿(1015)次运算,它工作103s可进行多少次运算?
求计算机工作103s可进行运算的次数,可列式为 .
观察发现,1015 和103这两个乘数的底数都是10,是同底数幂的形式.
我们把形如1015 ×103的这种运算叫作同底数幂的乘法.
1015 ×103
观察这个算式,它有何特点?
1015×103
新知探究
知识点 同底数幂的乘法
想一想该如何计算这个算式呢?
=(10×10×10 ×…×10)
15个10
×(10×10×10)
=10×10×…×10
18个10
=1018
(乘法的结合律)
(乘方的意义)
新知探究
知识点 同底数幂的乘法
(1)25×22=2 ( )
根据乘方的意义填空,观察计算结果,你能发现什么规律?
(2)a3·a2=a( )
(3)5m×5n =5( )(m,n是正整数)
新知探究
知识点 同底数幂的乘法
(1)25×22=2 ( )
=(2×2×2×2×2)
×(2×2)
=2×2×2×2×2×2×2
=27
(2)a3·a2=a( )
=(a﹒a﹒a) (a﹒a)
=a﹒a﹒a﹒a﹒a
=a5
7
5
7个2
5个a
新知探究
知识点 同底数幂的乘法
(3)5m×5n =5( )(m,n是正整数)
=(5×5×5×…×5)
m个5
×(5×5×5 ×…×5)
n个5
=5×5×…×5
(m+n)个5
=5m+n
m+n
新知探究
知识点 同底数幂的乘法
(3)5m×5n =5m+n(m,n是正整数)
(1)25×22=27
(2)a3·a2=a5
5和2相加得到7
3和2相加得到5
观察:计算前后,(1)底数有何变化
m和n相加得到m+n
(2)指数有何变化
底数没有变
两因数中的指数相加得到结果中的指数
新知探究
知识点 同底数幂的乘法
am · an =am+n
猜想:同底数幂相乘,底数不改变,只需把指数相加,字母表示为:
你能总结出同底数幂相乘的运算法则吗
新知探究
知识点 同底数幂的乘法
am · an =am+n
猜想:同底数幂相乘,底数不改变,只需把指数相加,字母表示为:
你能总结出同底数幂相乘的运算法则吗
新知探究
知识点 同底数幂的乘法
am·an
=(a·a·…·a)
m个a
(a·a·…·a)
n个a
=a·a·…·a
(m+n)个a
=am+n .
验证:一般地,对于任意底数a与任意正整数m,n,
·
新知探究
同底数幂的乘法法则:am · an =am+n (m,n都是正整数).
即同底数幂相乘,底数不变,指数相加.
使用该法则运算的前提条件有两个: ①乘法运算;②底数相同.
知识点 同底数幂的乘法
新知探究
am an ap = (m,n,p都为正整数).
am 表示m个a相乘,an表示n个a相乘,ap表示p个a相乘.
那么根据乘法的结合律可知am an ap 表示(m+n+p)个a相乘,即am+n+p.所以am an ap = am+n+p(m,n,p都为正整数).
同底数幂的乘法的性质也适用于三个及三个以上的同底数幂相乘,即am an ap =am+n+p(m,n,p都为正整数).
拓展点
知识点 同底数幂的乘法
新知探究
知识点 同底数幂的乘法
例1 计算:(1) x2 x5 ; (2) a a5 ;
(3) (-2)×(-2)4×(-2)3 ; (4) xm x3m+1 .
解: (1) x2 x5 = x2+5 = x7 ;
(2) a a5 = a1+5 = a6 ;
(3) (-2)×(-2)4×(-2)3 = (-2)1+4+3= (-2)8 = 256 ;
(4) xm x3m+1 = xm+3m+1 = x4m+1 .
a=a1
(-2)=(-2)1
新知探究
知识点 同底数幂的乘法
解:(1) (a+b)5 · (a+b)6 = (a+b)5+6 =(a+b)11;
(2)-x2 (-x)8 =-x2 x8=- x2+8=-x10;
(3)(x-y)2·(y-x)5=(y-x)2·(y-x)5
=(y-x)2+5=(y-x)7.
例2 计算:
(1)(a+b)5 · (a+b)6 ;
(3)(x-y)2·(y-x)5.
(2) -x2 (-x)8 ;
底数为多项式时,将多项式看成整体
底数互为相反数,先将底数化相同
(x-y)2=(y-x)2
或(y-x)5=-(x-y)5
或(x-y)2·(y-x)5=(x-y)2·[-(x-y)5]=-(x-y)7=(y-x)7.
新知探究
知识点 同底数幂的乘法
同底数幂的乘法运算时,应注意:
(1)底数不一定只是一个数或一个字母,也可以是单项式或多项式.
(2)当底数互为相反数时,先把底数化成相同底数,再进行计算.
(3)单独一个字母或数字可以看成指数为1的幂,运算时不能忽略.
(4)运算中,经常用到以下变形:
新知探究
am+n可以写成am和an的积的形式.
am · an=am+n
am+n = am · an
同底数幂乘法法则的逆用
知识点 同底数幂的乘法
新知探究
填一填:若xm =3 ,xn =2,那么,
(1)xm+n = × = × = ;
(2)x2m = × = × = ;
(3)x2m+n = × = × = .
xm
xn
6
3
2
xm
xm
3
3
9
x2m
xn
9
2
18
知识点 同底数幂的乘法
思考:可写成哪两个因式的乘积的形式?
课堂小结
同底数幂的乘法
法则
逆用
常用变形
同底数幂相乘,底数不变,指数相加
am·an=am+n (m,n都是正整数)
am·an·ap=am+n+p(m,n,p都是正整数)
am+n =am·an (m,n都是正整数)
1.下列计算正确的有( )
①x x3 x2=x5;②b2+b2=b4;③cm c5=x5m;④y5 y5=2y5
A.3个 B.2个 C.1个 D.0个
【解析】A.x x3 x2=x6,错误;B.b2+b2=2b2,错误;C.cm c5=cm+5,错误;D.y5 y5=y10,错误.没有计算正确的.故选D.
D
课堂训练
课堂训练
3.计算(x-y)n (y-x)2n的结果为( )
A.(x-y)3n B.(y-x)3n C.-(x-y)3n D.±(y-x)3n
【解析】(x-y)n (y-x)2n=(x-y)n (x-y)2n=(x-y)3n.故选A.
A
2.下列各式的结果不等于23m+2的是( )
A.23m×22 B.2m×22m+2
C.23m+2 D.2m+2×22m
C
课堂训练
4.若3m+1=243,则3m+2的值为( )
A.243 B.245 C.729 D.2187
【解析】∵3m+1=243,
∴3m+2=3m+1×3=243×3=729.
故选C.
C
逆用同底数幂的乘法公式,将所求代数式转化为几个已知因式的乘积的形式,然后再求值.
课堂训练
5.电子文件的大小常用B,KB,MB,CB等作为单位,其中1GB=210MB,1MB=210KB,1KB=210B.某视频文件的大小约为2GB.则2GB等于( )
A.232B B.231B C.230B D.430B
【解析】由题意,得2GB=2×210×210×210(B)=21+10+10+10(B)=231(B),故选B.
B
课堂训练
(2)x·x2·x( )=x7;
(3)xm·( )=x3m;
(4)-b( )·(-b)2=-b7.
4
x2m
6.填空:
(1)(a-b)2·(a-b)( )=(a-b)5;
3
5
课堂训练
8.(1)若xm+n=18,xm=3,求xn的值.
解:∵xm+n=xm xn=18,xm=3,∴xn=18÷3=6.
(3)3×27×9=32x-4,求x的值.
解:3×27×9=3×33×32=36=32x-4,∴2x-4=6.解得x=5.
(2)若an-3 a2n+1=a10,求n的值.
解:∵an-3 a2n+1=a10,∴n-3+(2n+1)=10,解得n=4.
关键是将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
第十四章 整式的乘法与因式分解
14.1 整式的乘法
14.1.1 同底数幂的乘法
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.理解并掌握同底数幂的乘法法则.(重点)
2.能够运用同底数幂的乘法法则进行相关计算.(难点)
新课导入
复习引入
我们把这种运算叫做乘方.
n个a
an
底数
幂
指数
新课导入
复习引入
请按照乘方的定义填空.
(1)54 =( ) ;
(2)12×12×12×12×12×12=( ) ;
(3) (-3)10的底数是 ,指数是 ;
(4)(b-a)2的底数是 ,指数是 .
5×5×5×5
10
2
-3
(b-a)
126
练一练
新知探究
知识点 同底数幂的乘法
问题 一种电子计算机每秒可进行1千万亿(1015)次运算,它工作103s可进行多少次运算?
求计算机工作103s可进行运算的次数,可列式为 .
观察发现,1015 和103这两个乘数的底数都是10,是同底数幂的形式.
我们把形如1015 ×103的这种运算叫作同底数幂的乘法.
1015 ×103
观察这个算式,它有何特点?
1015×103
新知探究
知识点 同底数幂的乘法
想一想该如何计算这个算式呢?
=(10×10×10 ×…×10)
15个10
×(10×10×10)
=10×10×…×10
18个10
=1018
(乘法的结合律)
(乘方的意义)
新知探究
知识点 同底数幂的乘法
(1)25×22=2 ( )
根据乘方的意义填空,观察计算结果,你能发现什么规律?
(2)a3·a2=a( )
(3)5m×5n =5( )(m,n是正整数)
新知探究
知识点 同底数幂的乘法
(1)25×22=2 ( )
=(2×2×2×2×2)
×(2×2)
=2×2×2×2×2×2×2
=27
(2)a3·a2=a( )
=(a﹒a﹒a) (a﹒a)
=a﹒a﹒a﹒a﹒a
=a5
7
5
7个2
5个a
新知探究
知识点 同底数幂的乘法
(3)5m×5n =5( )(m,n是正整数)
=(5×5×5×…×5)
m个5
×(5×5×5 ×…×5)
n个5
=5×5×…×5
(m+n)个5
=5m+n
m+n
新知探究
知识点 同底数幂的乘法
(3)5m×5n =5m+n(m,n是正整数)
(1)25×22=27
(2)a3·a2=a5
5和2相加得到7
3和2相加得到5
观察:计算前后,(1)底数有何变化
m和n相加得到m+n
(2)指数有何变化
底数没有变
两因数中的指数相加得到结果中的指数
新知探究
知识点 同底数幂的乘法
am · an =am+n
猜想:同底数幂相乘,底数不改变,只需把指数相加,字母表示为:
你能总结出同底数幂相乘的运算法则吗
新知探究
知识点 同底数幂的乘法
am · an =am+n
猜想:同底数幂相乘,底数不改变,只需把指数相加,字母表示为:
你能总结出同底数幂相乘的运算法则吗
新知探究
知识点 同底数幂的乘法
am·an
=(a·a·…·a)
m个a
(a·a·…·a)
n个a
=a·a·…·a
(m+n)个a
=am+n .
验证:一般地,对于任意底数a与任意正整数m,n,
·
新知探究
同底数幂的乘法法则:am · an =am+n (m,n都是正整数).
即同底数幂相乘,底数不变,指数相加.
使用该法则运算的前提条件有两个: ①乘法运算;②底数相同.
知识点 同底数幂的乘法
新知探究
am an ap = (m,n,p都为正整数).
am 表示m个a相乘,an表示n个a相乘,ap表示p个a相乘.
那么根据乘法的结合律可知am an ap 表示(m+n+p)个a相乘,即am+n+p.所以am an ap = am+n+p(m,n,p都为正整数).
同底数幂的乘法的性质也适用于三个及三个以上的同底数幂相乘,即am an ap =am+n+p(m,n,p都为正整数).
拓展点
知识点 同底数幂的乘法
新知探究
知识点 同底数幂的乘法
例1 计算:(1) x2 x5 ; (2) a a5 ;
(3) (-2)×(-2)4×(-2)3 ; (4) xm x3m+1 .
解: (1) x2 x5 = x2+5 = x7 ;
(2) a a5 = a1+5 = a6 ;
(3) (-2)×(-2)4×(-2)3 = (-2)1+4+3= (-2)8 = 256 ;
(4) xm x3m+1 = xm+3m+1 = x4m+1 .
a=a1
(-2)=(-2)1
新知探究
知识点 同底数幂的乘法
解:(1) (a+b)5 · (a+b)6 = (a+b)5+6 =(a+b)11;
(2)-x2 (-x)8 =-x2 x8=- x2+8=-x10;
(3)(x-y)2·(y-x)5=(y-x)2·(y-x)5
=(y-x)2+5=(y-x)7.
例2 计算:
(1)(a+b)5 · (a+b)6 ;
(3)(x-y)2·(y-x)5.
(2) -x2 (-x)8 ;
底数为多项式时,将多项式看成整体
底数互为相反数,先将底数化相同
(x-y)2=(y-x)2
或(y-x)5=-(x-y)5
或(x-y)2·(y-x)5=(x-y)2·[-(x-y)5]=-(x-y)7=(y-x)7.
新知探究
知识点 同底数幂的乘法
同底数幂的乘法运算时,应注意:
(1)底数不一定只是一个数或一个字母,也可以是单项式或多项式.
(2)当底数互为相反数时,先把底数化成相同底数,再进行计算.
(3)单独一个字母或数字可以看成指数为1的幂,运算时不能忽略.
(4)运算中,经常用到以下变形:
新知探究
am+n可以写成am和an的积的形式.
am · an=am+n
am+n = am · an
同底数幂乘法法则的逆用
知识点 同底数幂的乘法
新知探究
填一填:若xm =3 ,xn =2,那么,
(1)xm+n = × = × = ;
(2)x2m = × = × = ;
(3)x2m+n = × = × = .
xm
xn
6
3
2
xm
xm
3
3
9
x2m
xn
9
2
18
知识点 同底数幂的乘法
思考:可写成哪两个因式的乘积的形式?
课堂小结
同底数幂的乘法
法则
逆用
常用变形
同底数幂相乘,底数不变,指数相加
am·an=am+n (m,n都是正整数)
am·an·ap=am+n+p(m,n,p都是正整数)
am+n =am·an (m,n都是正整数)
1.下列计算正确的有( )
①x x3 x2=x5;②b2+b2=b4;③cm c5=x5m;④y5 y5=2y5
A.3个 B.2个 C.1个 D.0个
【解析】A.x x3 x2=x6,错误;B.b2+b2=2b2,错误;C.cm c5=cm+5,错误;D.y5 y5=y10,错误.没有计算正确的.故选D.
D
课堂训练
课堂训练
3.计算(x-y)n (y-x)2n的结果为( )
A.(x-y)3n B.(y-x)3n C.-(x-y)3n D.±(y-x)3n
【解析】(x-y)n (y-x)2n=(x-y)n (x-y)2n=(x-y)3n.故选A.
A
2.下列各式的结果不等于23m+2的是( )
A.23m×22 B.2m×22m+2
C.23m+2 D.2m+2×22m
C
课堂训练
4.若3m+1=243,则3m+2的值为( )
A.243 B.245 C.729 D.2187
【解析】∵3m+1=243,
∴3m+2=3m+1×3=243×3=729.
故选C.
C
逆用同底数幂的乘法公式,将所求代数式转化为几个已知因式的乘积的形式,然后再求值.
课堂训练
5.电子文件的大小常用B,KB,MB,CB等作为单位,其中1GB=210MB,1MB=210KB,1KB=210B.某视频文件的大小约为2GB.则2GB等于( )
A.232B B.231B C.230B D.430B
【解析】由题意,得2GB=2×210×210×210(B)=21+10+10+10(B)=231(B),故选B.
B
课堂训练
(2)x·x2·x( )=x7;
(3)xm·( )=x3m;
(4)-b( )·(-b)2=-b7.
4
x2m
6.填空:
(1)(a-b)2·(a-b)( )=(a-b)5;
3
5
课堂训练
8.(1)若xm+n=18,xm=3,求xn的值.
解:∵xm+n=xm xn=18,xm=3,∴xn=18÷3=6.
(3)3×27×9=32x-4,求x的值.
解:3×27×9=3×33×32=36=32x-4,∴2x-4=6.解得x=5.
(2)若an-3 a2n+1=a10,求n的值.
解:∵an-3 a2n+1=a10,∴n-3+(2n+1)=10,解得n=4.
关键是将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
