初中数学人教版八上 14.1.3积的乘方 同步课件(25张PPT)
文档属性
| 名称 | 初中数学人教版八上 14.1.3积的乘方 同步课件(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 965.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 22:16:45 | ||
图片预览








文档简介
(共25张PPT)
第十四章 整式的乘法与因式分解
14.1 整式的乘法
14.1.3 积的乘方
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.理解并掌握积的乘方法则,会运用积的乘方法则进行积的
乘方的运算.(重点)
2.掌握积的乘方法则的推导过程.(难点)
新课导入
复习引入
即am an= (m,n都是正整数).
同底数幂的乘法法则:同底数幂相乘,底数 ,指数 .
同底数幂的乘法的性质也适用于三个及三个以上的同底数幂相乘.即
am an ap= (m,n,p都是正整数).
am+n+p
不变
相加
am+n
同底数幂的乘法的逆应用:am+n= (m,n都是正整数).
am an
新课导入
复习引入
即(am)n= (m,n都是正整数).
幂的乘方法则:幂的乘方,底数 ,指数 .
幂的乘方的性质也适用于三个及三个以上的幂的乘方.
即[(am)n]p= (m,n,p都是正整数).
amnp
不变
相乘
amn
幂的乘方的逆应用:amn= 或 (m,n都是正整数).
(am)n
(an)m
新课导入
复习引入
练一练
填空:
(1) m4 m4= ; (m4)4= ;
(2) y2 y4 y3 = ; [(y2)4]3 = ;
(3) 已知a3=9,则a6= ;
m8
y9
81
m16
y24
新知探究
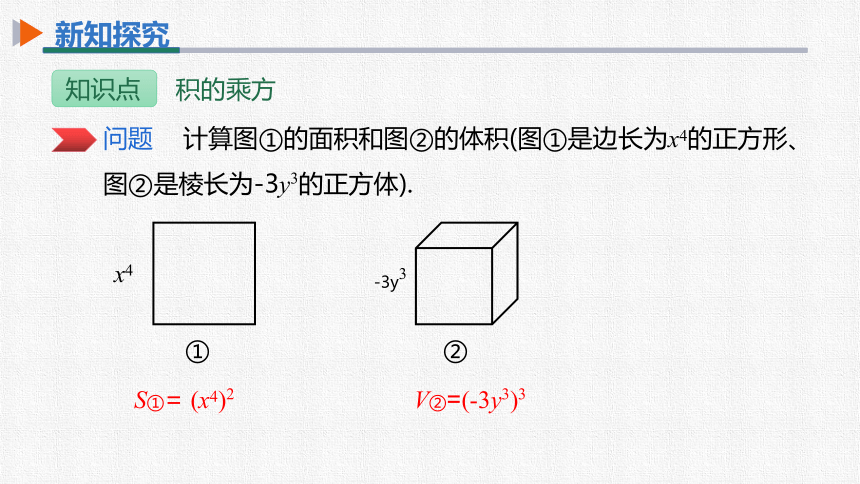
问题 计算图①的面积和图②的体积(图①是边长为x4的正方形、图②是棱长为-3y3的正方体).
①
②
x4
-3y3
S①= (x4)2
V②=(-3y3)3
知识点 积的乘方
新知探究
S①= (x4)2
V②=(-3y3)3
算式①的底数是幂的形式,是我们学过的幂的乘方;算式②的底数是两个因式的乘积的形式
我们把这样的算式叫做积的乘方
(1)比较这两个算式,它们有什么不同之处?
知识点 积的乘方
新知探究
知识点 积的乘方
V②=(-3y3)3
=(-3y3) (-3y3) (-3y3)
=(-3)×(-3)×(-3) y3 y3 y3
(同底数幂的乘法法则)
(乘方的意义)
=-27y9
=(-3)3 y9
(乘法交换律、结合律)
S①= (x4)2=x8
(幂的乘方)
(2)该如何计算这两个算式呢?
新知探究
填空,运算过程用到哪些运算律?运算结果又什么规律?
(1) (ab)2
= (ab) (ab)
=(a a) (b b)
=a( )b( ) ;
2
2
根据以上计算过程,类比同底数幂的乘法公式及幂的乘方公式,你能写出积的乘方公式吗 想一想:(ab)n=?
(2) (ab)3
=
=
=a( )b( ) .
(ab) (ab) (ab)
(a a a) (b b b)
3
3
(乘法交换律、结合律)
(同底数幂的乘法法则)
(乘方的意义)
知识点 积的乘方
新知探究
(ab)n
=(ab) (ab) … (ab)
n个ab
=a a … a b b … b
n个a
=anbn .
一般地,对于任意底数a,b与任意正整数n,
n个b
因此,我们有(ab)n=anbn (n为正整数).
知识点 积的乘方
新知探究
积的乘方法则:(ab)n=anbn (n为正整数).即积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
n
a
b
an
bn
知识点 积的乘方
积的乘方示例:
新知探究
例1 计算:
知识点 积的乘方
(1) (2a)3 ; (2) (-5b)3 ; (3) (xy2)2 ; (4) (-2x3)4 .
解:(1) (2a)3 =23·a3=8a3 ;
(2) (-5b)3 =(-5)3·b3=-125b3 ;
(3) (xy2)2 =x2·(y2)2=x2y4 ;
(4) (-2x3)4 =(-2)4·(x3)4=16x12 .
字母前的系数不要忘记乘方
新知探究
问题 (abc)n= (n为正整数).
积的乘方的性质也适用于三个及三个以上的因式的乘积的乘方,即(abc)n=an bncn(n为正整数).
拓展点
(abc)n
n个abc
n个b
=an bncn .
=(abc) (abc) … (abc)
知识点 积的乘方
=a a … a b b … b c c … c
n个a
n个c
新知探究
解:(1)(-3×102)3 = (-3)3×(102)3 = -27×106 =-2.7×107 ;
(2) (-x3y2z)6 = (-1)6·(x3)6 ·(y2)6·z6=x18y12z6 ;
将a+b看成整体
知识点 积的乘方
例2 计算:
(1)(-3×102)3 ; (2) (-x3y2z)6 ; (3) -[ (a+b)3 ]5 .
(3)-[ (a+b)3 ]5 = - ( )5·[(a+b)3]5=- (a+b)15 .
将“-”看成”-1”,作为一个因式去乘方
新知探究
运用积的乘方法则进行计算时,应注意:
(1)公式中的a、b可以是数字、字母、单项式或多项式;
(2)每个因式都要乘方,不能漏掉任何一个因式,尤其是字母前的系数,应连同它的符号一起乘方;
(3)当底数前为“-”时,应将其视为“-1”,作为一个因式去乘方;
(4)在积的乘方中,底数是乘积的形式,要避免出现(a+b)n=an+bn.
知识点 积的乘方
新知探究
an bn可以写成ab的n次方的形式
(ab)n=an bn(n为正整数)
an bn =(ab)n(n为正整数)
积的乘方法则的逆用
知识点 积的乘方
新知探究
知识点 积的乘方
例3 计算: .
解:
分析:由于 ,而这两个因式的指数分别为2021,2022,
故逆用积的乘方的性质可简化运算.
课堂小结
积的乘方
法则
逆用
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘
(ab)n=anbn (n为正整数)
(abc)n=an bncn(n为正整数)
an bn =(ab)n(n为正整数)
课堂训练
2. 计算(-5x3y)2正确的是( )
A.25x5y2 B.25x6y2 C.-5x3y2 D.-10x6y2
B
1. 下列运算正确的是( )
A.2a-a=2 B.(a2)3=a6 C.a2 a3=a6 D.(ab)2=ab2
B
课堂训练
(1)(2b2)3=2b6 ( )
×
×
×
(2) (3xy)3=9x3y3 ( )
×
(3) (-a2)2=-a4 ( )
(4) -(-ab2)2=a2b4 ( )
3.判断,并将错误的改正:
改正:8b6
改正:27x3y3
改正:a4
改正:-a2b4
(5) (-2x3y)3= -8x6y3 ( )
×
改正:-8x9y3
课堂训练
4.已学的“幂的运算”有:①同底数幂的乘法,②幂的乘方,③积的乘方.在“(a2 a3)2=(a2)2(a3)2=a4 a6=a10”的运算过程中,运用了上述幂的运算中的 (按运算顺序填序号).
③②①
课堂训练
【解析】∵am=2,bm=5,(ab)m=am bm,
∴(ab)m=2×5=10.故答案为10.
5.已知am=2,bm=5,则(ab)m= .
10
课堂训练
7.计算下列各题:
(3)(-2anb3n)2+(a2b6)n.
(2)(-3x3)2-(-x2)3+(-2x)2-(-x)3;
(1)a3 a4 a+(a2)4-(-2a4)2;
解:(1)原式=a3+4+1+a8-(-2)2×(a4)2=a8+a8-4a8=-2a8;
(2)原式=(-3)2×(x3)2-(-1)3×(x2)3+(-2)2×x2-(-x3)=9x6-(-x6)+4x2+x3=10x6+x3+4x2;
(3)原式=4a2nb6n+a2nb6n=5a2nb6n.
课堂训练
解:
方法一:(am an)2
=(am+n)2
=a2m+2n.
8.用两种方法计算(am an)2.
方法二:(am an)2
=a2m a2n
=a2m+2n.
课堂训练
9.若(4am+nbm)3=64a15b9成立,求m、n的值.
解:(4am+nbm)3 =43×(am+n)3×(bm)3
=64a3(m+n)b3m
=64a15b9 .
则3(m+n)=15,3m=9,解得m=3,n=2 .
第十四章 整式的乘法与因式分解
14.1 整式的乘法
14.1.3 积的乘方
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.理解并掌握积的乘方法则,会运用积的乘方法则进行积的
乘方的运算.(重点)
2.掌握积的乘方法则的推导过程.(难点)
新课导入
复习引入
即am an= (m,n都是正整数).
同底数幂的乘法法则:同底数幂相乘,底数 ,指数 .
同底数幂的乘法的性质也适用于三个及三个以上的同底数幂相乘.即
am an ap= (m,n,p都是正整数).
am+n+p
不变
相加
am+n
同底数幂的乘法的逆应用:am+n= (m,n都是正整数).
am an
新课导入
复习引入
即(am)n= (m,n都是正整数).
幂的乘方法则:幂的乘方,底数 ,指数 .
幂的乘方的性质也适用于三个及三个以上的幂的乘方.
即[(am)n]p= (m,n,p都是正整数).
amnp
不变
相乘
amn
幂的乘方的逆应用:amn= 或 (m,n都是正整数).
(am)n
(an)m
新课导入
复习引入
练一练
填空:
(1) m4 m4= ; (m4)4= ;
(2) y2 y4 y3 = ; [(y2)4]3 = ;
(3) 已知a3=9,则a6= ;
m8
y9
81
m16
y24
新知探究
问题 计算图①的面积和图②的体积(图①是边长为x4的正方形、图②是棱长为-3y3的正方体).
①
②
x4
-3y3
S①= (x4)2
V②=(-3y3)3
知识点 积的乘方
新知探究
S①= (x4)2
V②=(-3y3)3
算式①的底数是幂的形式,是我们学过的幂的乘方;算式②的底数是两个因式的乘积的形式
我们把这样的算式叫做积的乘方
(1)比较这两个算式,它们有什么不同之处?
知识点 积的乘方
新知探究
知识点 积的乘方
V②=(-3y3)3
=(-3y3) (-3y3) (-3y3)
=(-3)×(-3)×(-3) y3 y3 y3
(同底数幂的乘法法则)
(乘方的意义)
=-27y9
=(-3)3 y9
(乘法交换律、结合律)
S①= (x4)2=x8
(幂的乘方)
(2)该如何计算这两个算式呢?
新知探究
填空,运算过程用到哪些运算律?运算结果又什么规律?
(1) (ab)2
= (ab) (ab)
=(a a) (b b)
=a( )b( ) ;
2
2
根据以上计算过程,类比同底数幂的乘法公式及幂的乘方公式,你能写出积的乘方公式吗 想一想:(ab)n=?
(2) (ab)3
=
=
=a( )b( ) .
(ab) (ab) (ab)
(a a a) (b b b)
3
3
(乘法交换律、结合律)
(同底数幂的乘法法则)
(乘方的意义)
知识点 积的乘方
新知探究
(ab)n
=(ab) (ab) … (ab)
n个ab
=a a … a b b … b
n个a
=anbn .
一般地,对于任意底数a,b与任意正整数n,
n个b
因此,我们有(ab)n=anbn (n为正整数).
知识点 积的乘方
新知探究
积的乘方法则:(ab)n=anbn (n为正整数).即积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
n
a
b
an
bn
知识点 积的乘方
积的乘方示例:
新知探究
例1 计算:
知识点 积的乘方
(1) (2a)3 ; (2) (-5b)3 ; (3) (xy2)2 ; (4) (-2x3)4 .
解:(1) (2a)3 =23·a3=8a3 ;
(2) (-5b)3 =(-5)3·b3=-125b3 ;
(3) (xy2)2 =x2·(y2)2=x2y4 ;
(4) (-2x3)4 =(-2)4·(x3)4=16x12 .
字母前的系数不要忘记乘方
新知探究
问题 (abc)n= (n为正整数).
积的乘方的性质也适用于三个及三个以上的因式的乘积的乘方,即(abc)n=an bncn(n为正整数).
拓展点
(abc)n
n个abc
n个b
=an bncn .
=(abc) (abc) … (abc)
知识点 积的乘方
=a a … a b b … b c c … c
n个a
n个c
新知探究
解:(1)(-3×102)3 = (-3)3×(102)3 = -27×106 =-2.7×107 ;
(2) (-x3y2z)6 = (-1)6·(x3)6 ·(y2)6·z6=x18y12z6 ;
将a+b看成整体
知识点 积的乘方
例2 计算:
(1)(-3×102)3 ; (2) (-x3y2z)6 ; (3) -[ (a+b)3 ]5 .
(3)-[ (a+b)3 ]5 = - ( )5·[(a+b)3]5=- (a+b)15 .
将“-”看成”-1”,作为一个因式去乘方
新知探究
运用积的乘方法则进行计算时,应注意:
(1)公式中的a、b可以是数字、字母、单项式或多项式;
(2)每个因式都要乘方,不能漏掉任何一个因式,尤其是字母前的系数,应连同它的符号一起乘方;
(3)当底数前为“-”时,应将其视为“-1”,作为一个因式去乘方;
(4)在积的乘方中,底数是乘积的形式,要避免出现(a+b)n=an+bn.
知识点 积的乘方
新知探究
an bn可以写成ab的n次方的形式
(ab)n=an bn(n为正整数)
an bn =(ab)n(n为正整数)
积的乘方法则的逆用
知识点 积的乘方
新知探究
知识点 积的乘方
例3 计算: .
解:
分析:由于 ,而这两个因式的指数分别为2021,2022,
故逆用积的乘方的性质可简化运算.
课堂小结
积的乘方
法则
逆用
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘
(ab)n=anbn (n为正整数)
(abc)n=an bncn(n为正整数)
an bn =(ab)n(n为正整数)
课堂训练
2. 计算(-5x3y)2正确的是( )
A.25x5y2 B.25x6y2 C.-5x3y2 D.-10x6y2
B
1. 下列运算正确的是( )
A.2a-a=2 B.(a2)3=a6 C.a2 a3=a6 D.(ab)2=ab2
B
课堂训练
(1)(2b2)3=2b6 ( )
×
×
×
(2) (3xy)3=9x3y3 ( )
×
(3) (-a2)2=-a4 ( )
(4) -(-ab2)2=a2b4 ( )
3.判断,并将错误的改正:
改正:8b6
改正:27x3y3
改正:a4
改正:-a2b4
(5) (-2x3y)3= -8x6y3 ( )
×
改正:-8x9y3
课堂训练
4.已学的“幂的运算”有:①同底数幂的乘法,②幂的乘方,③积的乘方.在“(a2 a3)2=(a2)2(a3)2=a4 a6=a10”的运算过程中,运用了上述幂的运算中的 (按运算顺序填序号).
③②①
课堂训练
【解析】∵am=2,bm=5,(ab)m=am bm,
∴(ab)m=2×5=10.故答案为10.
5.已知am=2,bm=5,则(ab)m= .
10
课堂训练
7.计算下列各题:
(3)(-2anb3n)2+(a2b6)n.
(2)(-3x3)2-(-x2)3+(-2x)2-(-x)3;
(1)a3 a4 a+(a2)4-(-2a4)2;
解:(1)原式=a3+4+1+a8-(-2)2×(a4)2=a8+a8-4a8=-2a8;
(2)原式=(-3)2×(x3)2-(-1)3×(x2)3+(-2)2×x2-(-x3)=9x6-(-x6)+4x2+x3=10x6+x3+4x2;
(3)原式=4a2nb6n+a2nb6n=5a2nb6n.
课堂训练
解:
方法一:(am an)2
=(am+n)2
=a2m+2n.
8.用两种方法计算(am an)2.
方法二:(am an)2
=a2m a2n
=a2m+2n.
课堂训练
9.若(4am+nbm)3=64a15b9成立,求m、n的值.
解:(4am+nbm)3 =43×(am+n)3×(bm)3
=64a3(m+n)b3m
=64a15b9 .
则3(m+n)=15,3m=9,解得m=3,n=2 .
