初中数学人教版八上 14.2.2第1课时完全平方公式 同步课件(26张PPT)
文档属性
| 名称 | 初中数学人教版八上 14.2.2第1课时完全平方公式 同步课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 983.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 22:24:31 | ||
图片预览







文档简介
(共26张PPT)
第十四章 整式的乘法与因式分解
14.2 乘法公式
14.2.2 完全平方公式
第1课时 完全平方公式
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.了解并掌握完全平方公式及其结构特征.(重点)
2.理解完全平方公式的探索及推导过程,灵活应用完全平方公式进行计算和解决实际问题.(难点)
两个数的 与这两个数的 的积,等于这两个数的 .
新课导入
复习引入
和
差
平方差
(a+b)(a-b)= .
a2-b2
(1)什么是平方差公式?
(2)用语言怎么叙述?
新课导入
复习引入
练一练
填空:
(1)(x+y2)(x-y2)= ;
(2)(-1-b)(-1+b)= ;
(3)(a-2)(a+3)= .
1-b2
a2+a-6
x2-y4
(3)(p-1)2=(p-1)(p-1)= ;
(2)(m+2)2= ;
(1)(p+1)2=(p+1)(p+1)= ;
新知探究
知识点1 完全平方公式
p2+2p+1
m2+4m+4
p2-2p+1
(4)(m-2)2= .
m2-4m+4
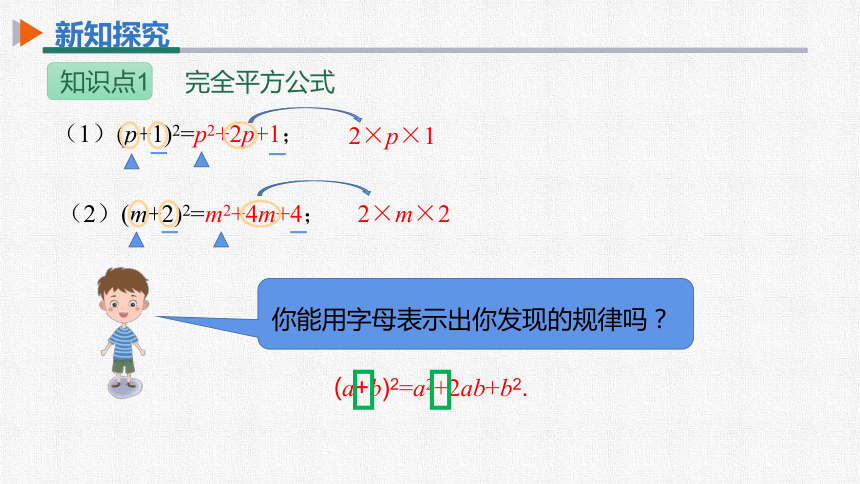
探究 计算下列多项式的积,你能发现什么规律?
(2)(m+2)2=m2+4m+4;
(1)(p+1)2=p2+2p+1;
新知探究
知识点1 完全平方公式
你能用字母表示出你发现的规律吗?
(a+b)2=a2+2ab+b2.
2×p×1
2×m×2
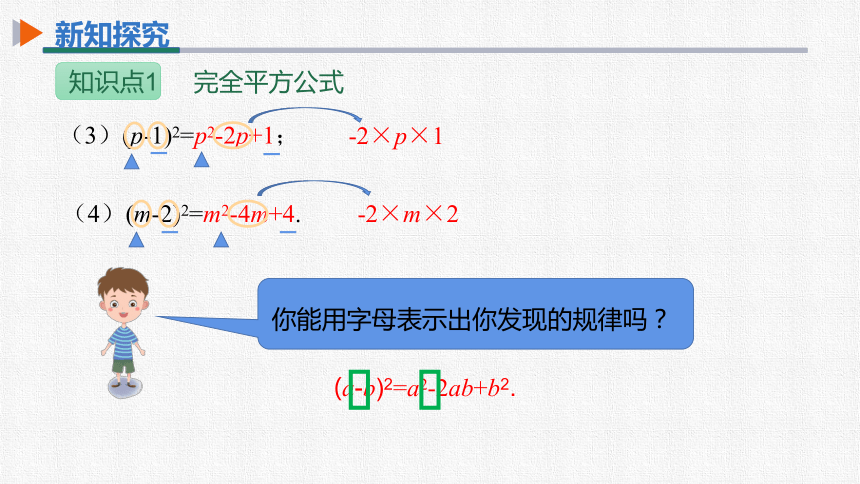
(4)(m-2)2=m2-4m+4.
(3)(p-1)2=p2-2p+1;
新知探究
知识点1 完全平方公式
你能用字母表示出你发现的规律吗?
(a-b)2=a2-2ab+b2.
-2×p×1
-2×m×2
新知探究
(a+b)2=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2.
推导方法一:用多项式乘多项式推导
(a-b)2=(a-b)(a-b)=a2-ab-ab+b2=a2-2ab+b2.
怎样验证这两个等式的正确性呢?
知识点1 完全平方公式
如图①,边长为(a+b) 的正方形的面积是 .
新知探究
所以(a+b)2=a2+2ab+b2.
推导方法二:借助几何图形推导
b
a
①
b
a
知识点1 完全平方公式
(a+b)2
a2
b2
ab
ab
它的面积还可以视为两个小正方形的面积与两个小长方形的面积的和,即
.
a2+ab+ab+b2=a2+2ab+b2
它的面积还可以视为大正方形的面积
减去两个小长方形与一个小正方形的面积和,即
.
所以(a-b)2=a2-2ab+b2.
新知探究
如图② ,边长为(a-b) 的正方形的面积是 .
a2
b
a
②
a
b
知识点1 完全平方公式
(a-b)2
(a-b)2
b(a-b)
b(a-b)
b2
a2-b(a-b)-b(a-b)-b2=a2-2ab+b2
新知探究
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
也就是说,两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
这两个公式叫做(乘法的)完全平方公式.
简记为:“首平方,尾平方,积的2倍放中央,符号确定看前方”
知识点1 完全平方公式
新知探究
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
完全平方公式的特点:
(1)两个公式的等号左边都是一个二项式的完全平方,两者仅有一个“符号”不同;
(2)两个公式的等号右边都是二次三项式,其中首尾两项是等号左边二项式中每一项的平方,中间一项是左边二项式中两项乘积的2倍,两者也仅有一个“符号”不同.
知识点1 完全平方公式
新知探究
完全平方公式计算的示例:
相加
a
b
2ab
a2
b2
a2
b2
2ab
b
a
相减
知识点1 完全平方公式
新知探究
解:(1)(4m+n)2=(4m)2+2·(4m)·n+n2=16m2+8mn+n2 ;
例1 运用完全平方公式计算:
(1) (4m+n)2 ; (2) (y- )2.
(2) (y- )2=y2-2·y· +( )2=y2-y+ .
知识点1 完全平方公式
选用“和”的完全平方公式.
选用“差”的完全平方公式.
新知探究
(1) 1022;
(2) 992.
例2 运用完全平方公式计算:
解:(1) 1022
= (100+2)2
=10000+400+4
=10404.
(2) 992
= (100–1)2
=10000-200+1
=9801.
=1002 +2×100×2+22
=1002–2×100×1+12
通过合理变形,利用完全平方公式,可以简化运算.
知识点1 完全平方公式
新知探究
跟踪训练
判断下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)(x+y)2=x2+y2
(2)(x-y)2=x2-y2
(3) (-x+y)2=x2+2xy+y2
(4) (2x+y)2=4x2+2xy+y2
×
×
×
×
(x+y)2 =x2+2xy+y2
(x-y)2 =x2 -2xy+y2
(-x+y)2 =x2 -2xy+y2
(2x+y)2 =4x2+4xy+y2
新知探究
运用完全平方公式进行计算时,应注意:
(1)公式中的字母a,b可以是单项式,也可以是多项式,只要符合这个公式的结构特征就可以运用这个公式;
(2)公式等号右边2ab的符号取决于等号左边二项式中两项的符号,若这两项同号,则2ab取“+”;若这两项异号,则2ab取“-”;
(3)(a±b)2 ≠ a2±b2 .
新知探究
例3 已知x-y=6,xy=-8.求:
(1)x2+y2的值;
(2)(x+y)2的值.
=36-16=20;
解:(1)∵x-y=6,xy=-8,(x-y)2=x2+y2-2xy,
∴x2+y2=(x-y)2+2xy=62+2×(-8)
(2)∵x2+y2=20,xy=-8,
∴(x+y)2=x2+y2+2xy=20-16=4.
你还有其他的解法吗?
方法二:
(x+y)2=(x-y)2+4xy
=62+4×(-8)
=36-32=4.
知识点2 完全平方公式的常见变形
课堂小结
平方差公式
符号表示
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
内容
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
注意事项
常见变形
课堂训练
2.下列计算结果为2ab-a2-b2的是( )
A.(a-b)2 B.(-a-b)2
C.-(a+b)2 D.-(a-b)2
D
1.下列各式中,与(x-1)2相等的是( )
A.x2-2x+1 B.x2-2x-1 C.x2-1 D.x2
A
3. 若多项式9x2+mx+1是一个完全平方式,则m的值是( )
A.±3 B.±6 C.3 D.±9
课堂训练
B
【解析】∵多项式9x2+mx+1是一个完全平方式,
∴9x2+mx+1=(3x+1)2或9x2+mx+1=(3x-1)2,
即9x2+mx+1=9x2+6x+1或9x2+mx+1=9x2-6x+1,
∴m=6或m=-6.故选B.
课堂训练
4.利用乘法公式判断,下列等式何者成立?( )
A.2482+248×52+522=3002
B.2482-248×48-482=2002
C.2482+2×248×52+522=3002
D.2482-2×248×48-482=2002
C
5. 若(2x+4y)2=4x2-2(m-1)xy+16y2,则m的值为 .
课堂训练
-7
【解析】(2x+4y)2=4x2+16xy+16y2,∴-2(m-1)=16,解得m=-7.故答案为-7.
6.利用完全平方公式计算:
解:(1)原式=(3m+4n)2
=9m2+24mn+16n2;
(1)(-3m-4n)2; (2)(-3a+b)2.
(2)原式=(b-3a)2
=b2-6ab+9a2.
课堂训练
7. 先化简,再求值:(x-3)2+(x+3)(x-3)+2x(2-x),其中x= .
解:原式=x2-6x+9+x2-9+4x-2x2
=-2x.
当x= 时,原式=-2×( )=1.
课堂训练
8.利用乘法公式计算:982-101×99.
解:原式=(100-2)2-(100+1)(100-1)
=1002-400+4-1002+1
=-395.
课堂训练
解:∵a+b=3,a-b=-1,
∴a2+2ab+b2=9①,a2-2ab+b2=1②,
①-②,得4ab=9-1=8,∴ab=2.
(2)已知a+b=3,且a-b=-1,求ab的值.
9.(1)已知x+y=8,xy=12,求x2-xy+y2的值.
解:∵x+y=8,xy=12,x2-xy+y2=(x+y)2-3xy
∴x2-xy+y2=82-3×12=64-36=28.
第十四章 整式的乘法与因式分解
14.2 乘法公式
14.2.2 完全平方公式
第1课时 完全平方公式
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.了解并掌握完全平方公式及其结构特征.(重点)
2.理解完全平方公式的探索及推导过程,灵活应用完全平方公式进行计算和解决实际问题.(难点)
两个数的 与这两个数的 的积,等于这两个数的 .
新课导入
复习引入
和
差
平方差
(a+b)(a-b)= .
a2-b2
(1)什么是平方差公式?
(2)用语言怎么叙述?
新课导入
复习引入
练一练
填空:
(1)(x+y2)(x-y2)= ;
(2)(-1-b)(-1+b)= ;
(3)(a-2)(a+3)= .
1-b2
a2+a-6
x2-y4
(3)(p-1)2=(p-1)(p-1)= ;
(2)(m+2)2= ;
(1)(p+1)2=(p+1)(p+1)= ;
新知探究
知识点1 完全平方公式
p2+2p+1
m2+4m+4
p2-2p+1
(4)(m-2)2= .
m2-4m+4
探究 计算下列多项式的积,你能发现什么规律?
(2)(m+2)2=m2+4m+4;
(1)(p+1)2=p2+2p+1;
新知探究
知识点1 完全平方公式
你能用字母表示出你发现的规律吗?
(a+b)2=a2+2ab+b2.
2×p×1
2×m×2
(4)(m-2)2=m2-4m+4.
(3)(p-1)2=p2-2p+1;
新知探究
知识点1 完全平方公式
你能用字母表示出你发现的规律吗?
(a-b)2=a2-2ab+b2.
-2×p×1
-2×m×2
新知探究
(a+b)2=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2.
推导方法一:用多项式乘多项式推导
(a-b)2=(a-b)(a-b)=a2-ab-ab+b2=a2-2ab+b2.
怎样验证这两个等式的正确性呢?
知识点1 完全平方公式
如图①,边长为(a+b) 的正方形的面积是 .
新知探究
所以(a+b)2=a2+2ab+b2.
推导方法二:借助几何图形推导
b
a
①
b
a
知识点1 完全平方公式
(a+b)2
a2
b2
ab
ab
它的面积还可以视为两个小正方形的面积与两个小长方形的面积的和,即
.
a2+ab+ab+b2=a2+2ab+b2
它的面积还可以视为大正方形的面积
减去两个小长方形与一个小正方形的面积和,即
.
所以(a-b)2=a2-2ab+b2.
新知探究
如图② ,边长为(a-b) 的正方形的面积是 .
a2
b
a
②
a
b
知识点1 完全平方公式
(a-b)2
(a-b)2
b(a-b)
b(a-b)
b2
a2-b(a-b)-b(a-b)-b2=a2-2ab+b2
新知探究
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
也就是说,两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
这两个公式叫做(乘法的)完全平方公式.
简记为:“首平方,尾平方,积的2倍放中央,符号确定看前方”
知识点1 完全平方公式
新知探究
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
完全平方公式的特点:
(1)两个公式的等号左边都是一个二项式的完全平方,两者仅有一个“符号”不同;
(2)两个公式的等号右边都是二次三项式,其中首尾两项是等号左边二项式中每一项的平方,中间一项是左边二项式中两项乘积的2倍,两者也仅有一个“符号”不同.
知识点1 完全平方公式
新知探究
完全平方公式计算的示例:
相加
a
b
2ab
a2
b2
a2
b2
2ab
b
a
相减
知识点1 完全平方公式
新知探究
解:(1)(4m+n)2=(4m)2+2·(4m)·n+n2=16m2+8mn+n2 ;
例1 运用完全平方公式计算:
(1) (4m+n)2 ; (2) (y- )2.
(2) (y- )2=y2-2·y· +( )2=y2-y+ .
知识点1 完全平方公式
选用“和”的完全平方公式.
选用“差”的完全平方公式.
新知探究
(1) 1022;
(2) 992.
例2 运用完全平方公式计算:
解:(1) 1022
= (100+2)2
=10000+400+4
=10404.
(2) 992
= (100–1)2
=10000-200+1
=9801.
=1002 +2×100×2+22
=1002–2×100×1+12
通过合理变形,利用完全平方公式,可以简化运算.
知识点1 完全平方公式
新知探究
跟踪训练
判断下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)(x+y)2=x2+y2
(2)(x-y)2=x2-y2
(3) (-x+y)2=x2+2xy+y2
(4) (2x+y)2=4x2+2xy+y2
×
×
×
×
(x+y)2 =x2+2xy+y2
(x-y)2 =x2 -2xy+y2
(-x+y)2 =x2 -2xy+y2
(2x+y)2 =4x2+4xy+y2
新知探究
运用完全平方公式进行计算时,应注意:
(1)公式中的字母a,b可以是单项式,也可以是多项式,只要符合这个公式的结构特征就可以运用这个公式;
(2)公式等号右边2ab的符号取决于等号左边二项式中两项的符号,若这两项同号,则2ab取“+”;若这两项异号,则2ab取“-”;
(3)(a±b)2 ≠ a2±b2 .
新知探究
例3 已知x-y=6,xy=-8.求:
(1)x2+y2的值;
(2)(x+y)2的值.
=36-16=20;
解:(1)∵x-y=6,xy=-8,(x-y)2=x2+y2-2xy,
∴x2+y2=(x-y)2+2xy=62+2×(-8)
(2)∵x2+y2=20,xy=-8,
∴(x+y)2=x2+y2+2xy=20-16=4.
你还有其他的解法吗?
方法二:
(x+y)2=(x-y)2+4xy
=62+4×(-8)
=36-32=4.
知识点2 完全平方公式的常见变形
课堂小结
平方差公式
符号表示
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
内容
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
注意事项
常见变形
课堂训练
2.下列计算结果为2ab-a2-b2的是( )
A.(a-b)2 B.(-a-b)2
C.-(a+b)2 D.-(a-b)2
D
1.下列各式中,与(x-1)2相等的是( )
A.x2-2x+1 B.x2-2x-1 C.x2-1 D.x2
A
3. 若多项式9x2+mx+1是一个完全平方式,则m的值是( )
A.±3 B.±6 C.3 D.±9
课堂训练
B
【解析】∵多项式9x2+mx+1是一个完全平方式,
∴9x2+mx+1=(3x+1)2或9x2+mx+1=(3x-1)2,
即9x2+mx+1=9x2+6x+1或9x2+mx+1=9x2-6x+1,
∴m=6或m=-6.故选B.
课堂训练
4.利用乘法公式判断,下列等式何者成立?( )
A.2482+248×52+522=3002
B.2482-248×48-482=2002
C.2482+2×248×52+522=3002
D.2482-2×248×48-482=2002
C
5. 若(2x+4y)2=4x2-2(m-1)xy+16y2,则m的值为 .
课堂训练
-7
【解析】(2x+4y)2=4x2+16xy+16y2,∴-2(m-1)=16,解得m=-7.故答案为-7.
6.利用完全平方公式计算:
解:(1)原式=(3m+4n)2
=9m2+24mn+16n2;
(1)(-3m-4n)2; (2)(-3a+b)2.
(2)原式=(b-3a)2
=b2-6ab+9a2.
课堂训练
7. 先化简,再求值:(x-3)2+(x+3)(x-3)+2x(2-x),其中x= .
解:原式=x2-6x+9+x2-9+4x-2x2
=-2x.
当x= 时,原式=-2×( )=1.
课堂训练
8.利用乘法公式计算:982-101×99.
解:原式=(100-2)2-(100+1)(100-1)
=1002-400+4-1002+1
=-395.
课堂训练
解:∵a+b=3,a-b=-1,
∴a2+2ab+b2=9①,a2-2ab+b2=1②,
①-②,得4ab=9-1=8,∴ab=2.
(2)已知a+b=3,且a-b=-1,求ab的值.
9.(1)已知x+y=8,xy=12,求x2-xy+y2的值.
解:∵x+y=8,xy=12,x2-xy+y2=(x+y)2-3xy
∴x2-xy+y2=82-3×12=64-36=28.
