浙江省温州市瓯海中学2013-2014学年高二下数学(文)会考练习
文档属性
| 名称 | 浙江省温州市瓯海中学2013-2014学年高二下数学(文)会考练习 |  | |
| 格式 | zip | ||
| 文件大小 | 217.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-27 08:23:53 | ||
图片预览


文档简介
浙江省温州市瓯海中学2013-2014学年高二下数学(文)会考练习
第I卷(选择题)
一.选择题
1.若集合, , ( )
A. B. C. D.
2.函数的定义域是( )
A. B. C. D.
3.过点P和Q的直线斜率为1,那么的值为( )
A.1 B.4 C.1或3 D.1或4
4.直线与圆相交所得线段的长度为 ( )
A. B. C. D.
5.已知角θ的终边上有一点 P(-4,3) , 则/的值是 ( )
A./ B./ C. D.
6.已知函数,,若,则( )
A.1 B. 2 C. 3 D. -1
7.椭圆/的离心率为( )
A./ B. C. D.
8.在等差数列{an}中,a1+a9=10,则a5的值为( ).
A.5 B.6 C.8 D.10
9.函数y=cos 2x在下列哪个区间上是减函数( )
A. B./ C./ D./
10.下列函数中,既是偶函数又在区间上存在零点的是( )
A./ B./ C./ D./
11.已知是两条不同直线, 是三个不同平面,则下列正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
12.已知a、b为单位向量,其夹角为60,则(2a-b)·b =( )
A. -1 B. 0 C. 1 D.2
13.设/,则“/”是“/”的( )
(A)充分条件 (B)必要条件
(C)充分必要条件 (D)既非充分又非必要条件
14.已知角/为第二象限角,/则/ ( )
A. B. C. D.
15.为了得到/的图象,只需将/的图象 ( )
A.向右平移/个长度单位 B.向右平移/个长度单位
C.向左平移/个长度单位 D.向左平移/个长度单位
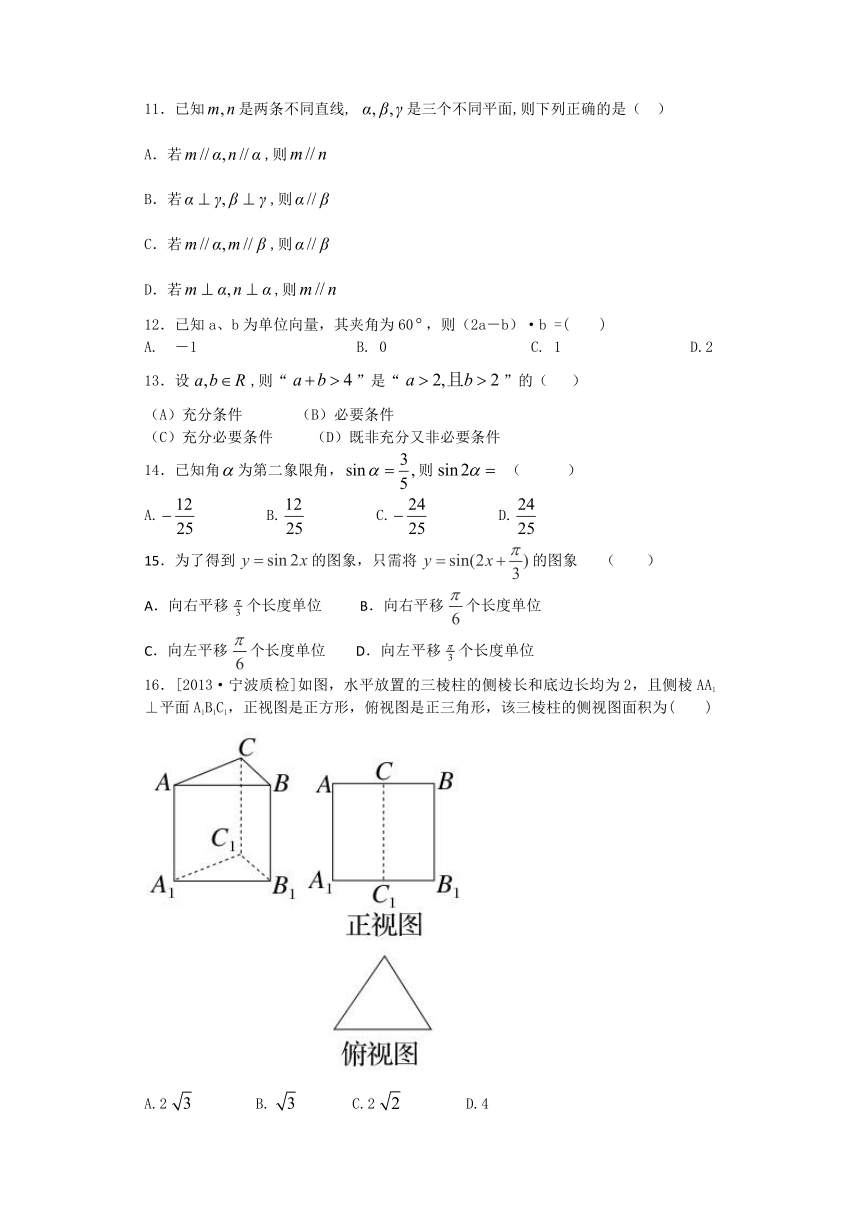
16.[2013·宁波质检]如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥平面A1B1C1,正视图是正方形,俯视图是正三角形,该三棱柱的侧视图面积为( )
/
A.2/ B./ C.2/ D.4
17.若变量/、/满足约束条件/,则/的最大值是( )
A.2 B.4 C.7 D.8
18.已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值是( )
A.3 B.4 C. D.
19. 双曲线:/的渐近线方程是( )
A./ B./ C./ D./
20.2log510+log50.25=( )
A.0 B.1 C.2 D.4
21.设等比数列/的前/项和为/,且/,/,则( )
A.60 B.70 C.90 D.40
22.如图所示,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是 ( ).
/
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
23.如图,半径为2的⊙O中,∠AOB=90°,D为OB的中点,AD的延长线交⊙O于点E,则线段DE的长为( )
/
A./ B./ C./ D./
24.若双曲线:与抛物线的准线交于两点,且,则的值是( )
A. B. .C. D.
25.已知的面积为,/,则/的周长等于 ( )
A./ B./ C./ D./
第II卷(非选择题)
评卷人
得分
二、填空题
26.不等式的解集为____________.
27.已知,,则________.
28.设/是公差不为零的等差数列,/且/成等比数列,则/ .
29.在?ABCD中,=a,=b,=3,M为BC的中点,则=______(用a,b表示).
30.已知二面角α―ΑΒ―β为600,在平面β内有一点P,它到棱AB的距离为2,则点P到平面α的距离为
评卷人
得分
三、解答题
31.已知数列是等差数列,且,.
⑴ 求数列的通项公式;
⑵ 令,求数列的前项和.
32.如图,在△/中,已知/,D是BC边上一点,AD=10,AC=14,DC=6,求AB的长.
/
33.如图,在五面体中,已知平面,,,,.
/
(1)求证:;
(2)求三棱锥的体积.
34.已知曲线上任意一点到两个定点,的距离之和为4.
(1)求曲线的方程;
(2)设过(0,-2)的直线与曲线交于两点,且(为原点),求直线的方程.
参考答案
1.A
2.D
3./
4.D
5.B
6.A
7.B
8.A
9.C
10.C
11.
12.B
13.B
14.C
15.B
16.A
17.C
18.B
19.D
20.C
21.B
22.D
23.C
24.D
25.C
26.
27.
28.
29.-a+b
30.
31.(1)2n, (2)
32./
33.(1)BC//AD得BC//平面ADEF得BC//EF,(2)
34.(1) /
(2)直线/的方程是/或/.
第I卷(选择题)
一.选择题
1.若集合, , ( )
A. B. C. D.
2.函数的定义域是( )
A. B. C. D.
3.过点P和Q的直线斜率为1,那么的值为( )
A.1 B.4 C.1或3 D.1或4
4.直线与圆相交所得线段的长度为 ( )
A. B. C. D.
5.已知角θ的终边上有一点 P(-4,3) , 则/的值是 ( )
A./ B./ C. D.
6.已知函数,,若,则( )
A.1 B. 2 C. 3 D. -1
7.椭圆/的离心率为( )
A./ B. C. D.
8.在等差数列{an}中,a1+a9=10,则a5的值为( ).
A.5 B.6 C.8 D.10
9.函数y=cos 2x在下列哪个区间上是减函数( )
A. B./ C./ D./
10.下列函数中,既是偶函数又在区间上存在零点的是( )
A./ B./ C./ D./
11.已知是两条不同直线, 是三个不同平面,则下列正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
12.已知a、b为单位向量,其夹角为60,则(2a-b)·b =( )
A. -1 B. 0 C. 1 D.2
13.设/,则“/”是“/”的( )
(A)充分条件 (B)必要条件
(C)充分必要条件 (D)既非充分又非必要条件
14.已知角/为第二象限角,/则/ ( )
A. B. C. D.
15.为了得到/的图象,只需将/的图象 ( )
A.向右平移/个长度单位 B.向右平移/个长度单位
C.向左平移/个长度单位 D.向左平移/个长度单位
16.[2013·宁波质检]如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥平面A1B1C1,正视图是正方形,俯视图是正三角形,该三棱柱的侧视图面积为( )
/
A.2/ B./ C.2/ D.4
17.若变量/、/满足约束条件/,则/的最大值是( )
A.2 B.4 C.7 D.8
18.已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值是( )
A.3 B.4 C. D.
19. 双曲线:/的渐近线方程是( )
A./ B./ C./ D./
20.2log510+log50.25=( )
A.0 B.1 C.2 D.4
21.设等比数列/的前/项和为/,且/,/,则( )
A.60 B.70 C.90 D.40
22.如图所示,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是 ( ).
/
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
23.如图,半径为2的⊙O中,∠AOB=90°,D为OB的中点,AD的延长线交⊙O于点E,则线段DE的长为( )
/
A./ B./ C./ D./
24.若双曲线:与抛物线的准线交于两点,且,则的值是( )
A. B. .C. D.
25.已知的面积为,/,则/的周长等于 ( )
A./ B./ C./ D./
第II卷(非选择题)
评卷人
得分
二、填空题
26.不等式的解集为____________.
27.已知,,则________.
28.设/是公差不为零的等差数列,/且/成等比数列,则/ .
29.在?ABCD中,=a,=b,=3,M为BC的中点,则=______(用a,b表示).
30.已知二面角α―ΑΒ―β为600,在平面β内有一点P,它到棱AB的距离为2,则点P到平面α的距离为
评卷人
得分
三、解答题
31.已知数列是等差数列,且,.
⑴ 求数列的通项公式;
⑵ 令,求数列的前项和.
32.如图,在△/中,已知/,D是BC边上一点,AD=10,AC=14,DC=6,求AB的长.
/
33.如图,在五面体中,已知平面,,,,.
/
(1)求证:;
(2)求三棱锥的体积.
34.已知曲线上任意一点到两个定点,的距离之和为4.
(1)求曲线的方程;
(2)设过(0,-2)的直线与曲线交于两点,且(为原点),求直线的方程.
参考答案
1.A
2.D
3./
4.D
5.B
6.A
7.B
8.A
9.C
10.C
11.
12.B
13.B
14.C
15.B
16.A
17.C
18.B
19.D
20.C
21.B
22.D
23.C
24.D
25.C
26.
27.
28.
29.-a+b
30.
31.(1)2n, (2)
32./
33.(1)BC//AD得BC//平面ADEF得BC//EF,(2)
34.(1) /
(2)直线/的方程是/或/.
同课章节目录
