冀教版七年级下册数学第九章第2节《三角形内角和外角(1)》参考课件(共10张PPT)
文档属性
| 名称 | 冀教版七年级下册数学第九章第2节《三角形内角和外角(1)》参考课件(共10张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 827.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-26 08:56:42 | ||
图片预览




文档简介
课件10张PPT。9.2三角形内角和外角(一)三角形的内角和定理
三角形的三个内角等于180°.已知:如图△ABC.
求证:∠A +∠B+∠C=180°12AB3C已知:如图,△ABC.
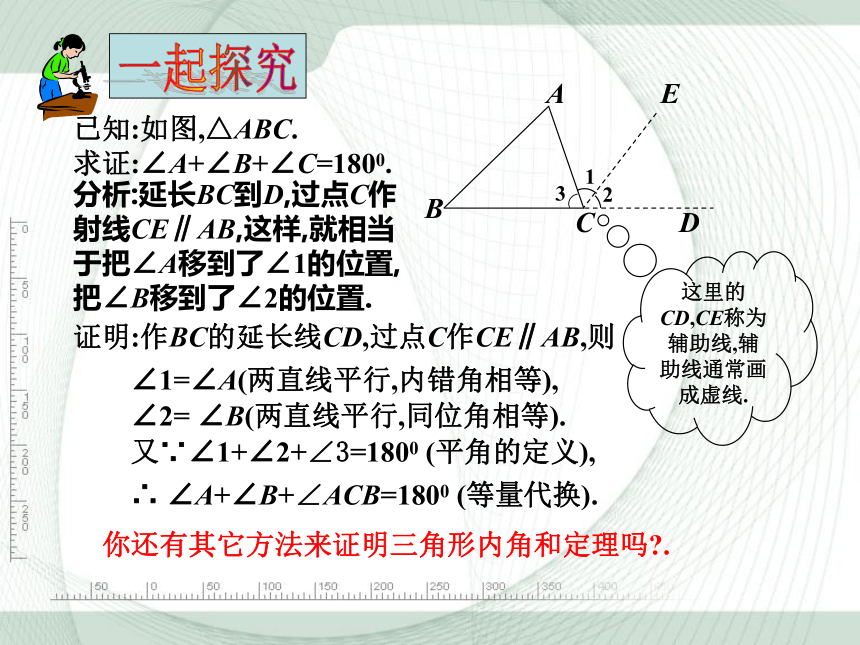
求证:∠A+∠B+∠C=1800.证明:作BC的延长线CD,过点C作CE∥AB,则 你还有其它方法来证明三角形内角和定理吗?. ∠1=∠A(两直线平行,内错角相等), ∠2= ∠B(两直线平行,同位角相等). 又∵∠1+∠2+∠3=1800 (平角的定义), ∴ ∠A+∠B+∠ACB=1800 (等量代换).分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.这里的CD,CE称为辅助线,辅助线通常画成虚线.ABC在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可以吗?请你帮小明把想法化为实际行动.小明的想法已经变为现实,由此你受到什么启发?你有新的证法吗?证明:过点A作PQ∥BC,则ABC ∠1=∠B(两直线平行,内错角相等), ∠2=∠C(两直线平行,内错角相等), 又∵∠1+∠2+∠3=1800 (平角的定义), ∴ ∠BAC+∠B+∠C=1800 (等量代换).所作的辅助线是证明的一个重要组成部分,要在证明时首先叙述出来.2根据下面的图形,写出相应的证明. 你还能想出其它证法吗?三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.已知:如图在△ABC中,DE∥BC,∠A=600, ∠C=700.
求证: ∠ADE=500.DCBAE如图,已知∠AMN+∠MNF+∠NFC=360°,
求证:AB∥CD.再见
三角形的三个内角等于180°.已知:如图△ABC.
求证:∠A +∠B+∠C=180°12AB3C已知:如图,△ABC.
求证:∠A+∠B+∠C=1800.证明:作BC的延长线CD,过点C作CE∥AB,则 你还有其它方法来证明三角形内角和定理吗?. ∠1=∠A(两直线平行,内错角相等), ∠2= ∠B(两直线平行,同位角相等). 又∵∠1+∠2+∠3=1800 (平角的定义), ∴ ∠A+∠B+∠ACB=1800 (等量代换).分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.这里的CD,CE称为辅助线,辅助线通常画成虚线.ABC在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可以吗?请你帮小明把想法化为实际行动.小明的想法已经变为现实,由此你受到什么启发?你有新的证法吗?证明:过点A作PQ∥BC,则ABC ∠1=∠B(两直线平行,内错角相等), ∠2=∠C(两直线平行,内错角相等), 又∵∠1+∠2+∠3=1800 (平角的定义), ∴ ∠BAC+∠B+∠C=1800 (等量代换).所作的辅助线是证明的一个重要组成部分,要在证明时首先叙述出来.2根据下面的图形,写出相应的证明. 你还能想出其它证法吗?三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.已知:如图在△ABC中,DE∥BC,∠A=600, ∠C=700.
求证: ∠ADE=500.DCBAE如图,已知∠AMN+∠MNF+∠NFC=360°,
求证:AB∥CD.再见
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
