分式方程的应用(河北省唐山市)

课件25张PPT。思考：知识拓展1、关于x的方程 有
增根，则增根是 （ ）
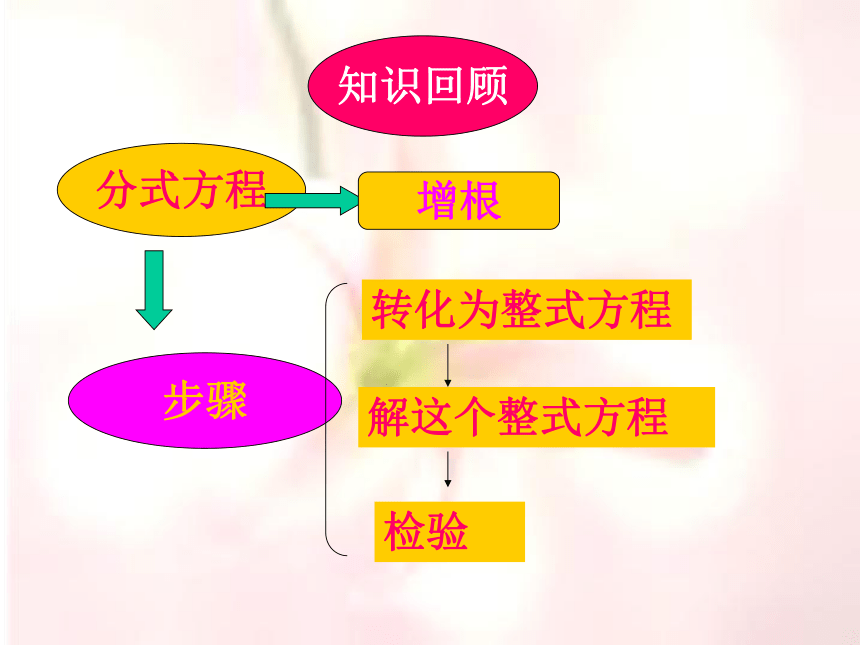
知识回顾分式方程步骤转化为整式方程解这个整式方程检验增根 数学世界应该是一个让你感到幸福和快乐的世界，希望你能体会到数学的好，数学给你带来得美！祝同学们学习进步！学有所得！23.2分式方程的应用引入问题：
轮船在顺水中航行80千米所需的时间和逆水航行60千米所需的时间相同.已知水流的速度是3千米/时，求轮船在静水中的速度.分析：
设轮船在静水中的速度为x千米/时，根据题意，得这个方程有何特点？ 面对日益严重的土地沙化问题，某县决定分期分批固沙造林，一期工程计划在一定期限内固沙造林2400公顷，实际每月固沙造林的面积比原计划多30公顷，结果提前4个月完成原计划任务.原计划每月固沙造林多少公顷？解：设原计划每月固沙造林x公顷,
根据题意得：练习：某工程队需要在规定日期内完成。若甲队单独做
正好按时完成；若乙队单独做，超过规定日期三天
才能完成。现由甲、乙合作两天，余下工程由乙队
单独做，恰好按期完成，问规定日期是多少天？解；设规定日期是x天，根据题意，得：方程两边同乘以x（x+3），得：2（x＋3）＋x2=x（x＋3）解得： x=6检验：x＝6时x（x+3）≠0，x＝6是原方程的解。答：规定日期是6天。例1:某工程队承建一所学校,在施工过程中,由于改进了工作方法.工作效率提高了20%,因此,比原定工期提前一个月完工,问这个工程队原计划用几个月建成这所希望学校?列方程解应用题的一般步骤是什么？1）、审清题意；
2）、设未知数；
3）、列式子，找出等量关系，建立方程；
4）、解方程；
5）、检查方程的解是否符合题意；
6）、作答。这些解题方法与步骤，对于学习分式方程应用题也适用吗? 这节课，我们将学习列分式方程解应用题。 1、为了帮助遭受自然灾害的地区重建家园，我校初中团总支号召同学们爱心捐款。已知第一次捐款总额为4800元，第二次款总额为5000元，第二次捐款人数比第一次多20人，而且两次人均捐款额恰好相等。你会求第一次捐款人数为多少人吗聪明的你，是否发现数学就在你身边？ 问题：某校招生录取时，为了防止数据输入出错，2640名学生的成绩数据分别由两位程序操作员各向计算机输入一遍，然后让计算机比较两人的输入是否一致.已知甲的输入速度是乙的2倍，结果甲比乙少用2小时输完.问这两个操作员每分钟各能输入多少名学生的成绩？例题讲解1列方程解应用题的步骤是怎样的呢？ 例题讲解1：某校招生录取时，为了防止数据输入出错，2640名学生的成绩数据分别由两位程序操作员各向计算机输入一遍，然后让计算机比较两人的输入是否一致.已知甲的输入速度是乙的2倍，结果甲比乙少用2小时输完.问这两个操作员每分钟各能输入多少名学生的成绩？分式方程的应用探索问题引入的解决：解　设乙每分钟能输入x名学生的成绩，则甲每分能输入2x名学生的成绩，根据题意得解得　x＝11 经检验，x＝11是原方程的解.并且x＝11，2x＝2×11＝22，符合题意.答：甲每分钟能输入22名学生的成绩，乙每分钟能输入11名学生的成绩. 强调：既要检验所求的解是否是原分式方程的解，还要检验是否符合题意；时间要统一。训练1. 滨河中学初二年级的学生到距学校15千米的风景区秋游，
一部分人骑自行车先走，40分钟后，其余的人乘汽车出发，结果
他们同时到达，已知汽车的速度是自行车的3倍，求两车的速度．学校自行车先走了40分钟A风景区X153X15分析;设自行车的速度是x千米/时汽车所用时间 – 自行车所用时间 = 汽车才开始走训练1滨河中学初二年级的学生到距学校15千米的风景区秋游，
一部分人骑自行车先走，40分钟后，其余的人乘汽车出发，结果
他们同时到达，已知汽车的速度是自行车的3倍，求两车的速度．解:设自行车的速度为x千米/时，那么汽车的速度为3x千米/时．依题意，得
解得 x = 15经检验, 15是原方程的解. 答:自行车的速度为15 千米/时，汽车的速度为45 千米/时． 2.小民和小强到校办工厂实习，两人各要做某种零件15个，小民先做，过了40分钟，小强才开始做，由于小强技术熟练，结果他们同时做完。已知小强每小时做零件的个数是小民的3倍，求小强、小民每小时各做多少个？ 解:设甲每小时做x个,则乙每小时做3x个,
依题意得:分析：这是一个工作量的问题 甲、乙两人做某种机器零件，已知甲每小时比乙多做6个，甲做90个零件所用的时间和乙做60个零件所用时间相等，求甲、乙每小时各做多少个零件？解：设甲每小时做x个零件则乙每小时做（ x －6）个零件，
依题意得： 经检验X=15是原方程的根。答：甲每小时做18个，乙每小时12个请审题分析题意
设元我们所列的是一个分式方程，这是分式方程的应用由x＝18得x－6=12等量关系：甲用时间=乙用时间例1：农机厂到距工厂15千米的向阳村检修农机，一部分人骑自行车先走，过了40分钟，其余人乘汽车去，结果他们同时到达，已知汽车的速度是自行车的3倍，求两车的速度。请审题分析题意分析：设自行车的速度是x千米/时，汽车的速度是3x千米/时请根据题意填写速度、时间、路程之间的关系表x3x1515请找出可列方程的等量关系农机厂某地BC自行车先走 时同时到达行程问题基本关系：S=vt解：设自行车的速度为x千米/时，那么汽车的速度是3x千米/时，
依题意得：汽车所用的时间＝自行车所用时间－ 时设元时单位一定要准确即：15＝45－2x2x=30 x=15经检验，15是原方程的根由x＝15得3x=45答：自行车的速度是15千米/时，汽车的速度是45千米/时得到结果记住要检验。例1：农机厂到距工厂15千米的向阳村检修农机，一部分人骑自行车先走，过了40分钟，其余人乘汽车去，结果他们同时到达，已知汽车的速度是自行车的3倍，求两车的速度。总结：列分式方程解应用题的方法和步骤如下：问题：请分析列分式方程解应用题与以前学习的列方程解应用题有什么区别？1：审题分析题意
2：设未知数
3：根据题意找相等关系，列出方程；
4：解方程，并验根（对解分式方程尤为重要）
5：写答案区别：解方程后要检验。动动脑本题还有其它解法吗？等量关系间接设未知数如：设汽车走这段路需x小时，则自行车需 1、 甲、乙两人练习骑自行车，已知甲每小时比乙多走6千米，甲骑90千米所用的时间和乙起骑60千米所用时间相等，求甲、乙每小时各骑多少千米？ 2、甲、乙两种商品，已知甲的价格每件比乙多6元，买甲90件所用的钱和买乙60件所用钱相等，求甲、乙每件商品的价格各多少元？试一试议一议 甲、乙两人做某种机器零件，已知甲每小时比乙多做6个，甲做90个零件所用的时间和乙做60个零件所用时间相等，求甲、乙每小时各做多少个零件？ 1、 甲、乙两人练习骑自行车，已知甲每小时比乙多走6千米，甲骑90千米所用的时间和乙起骑60千米所用时间相等，求甲、乙每小时各骑多少千米？ 2、甲、乙两种商品，已知甲的价格每件比乙多6元，买甲90件所用的钱和买乙60件所用钱相等，求甲、乙每件商品的价格各多少元？有什么区别和联系？联系数量关系和所列方程相同即：两个量的积等于第三个量区别一是工作问题，二是行程问题，三是价格问题总结：1、列分式方程解应用题，应该注意解题的五个步骤。2、列方程的关键是要在准确设元（可直接设，也可间节设）的前提下找出等量关系。3、解题过程注意画图或列表帮助分析题意找等量关系。4、注意不要漏检验和写答案。请同学总结该节课学习的内容