镶嵌
图片预览






文档简介
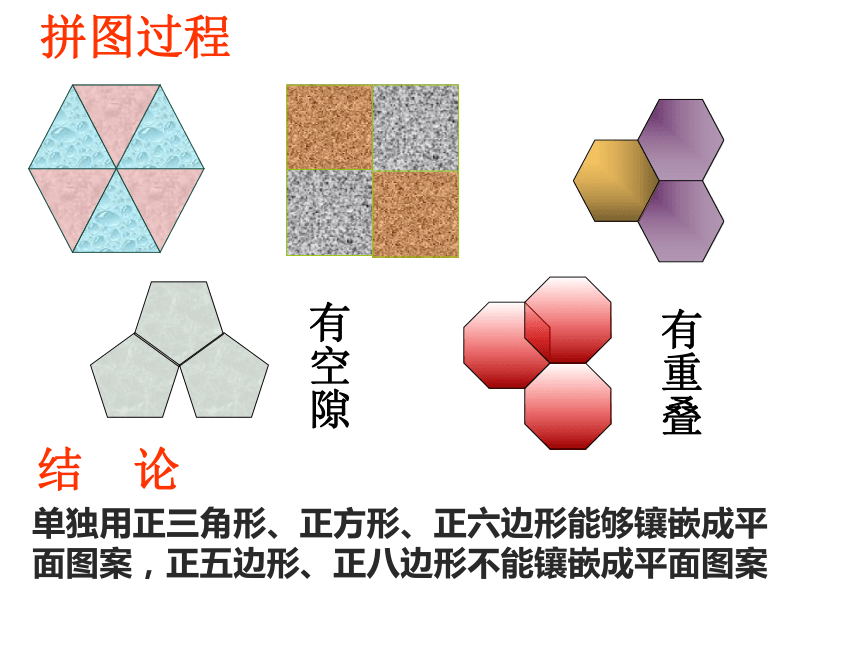
课件27张PPT。课题学习--- 镶嵌观察:地砖与地砖在拼接时有什么特点呢?用多边形把平面的一部分既无空隙又不重叠地全部覆盖,叫做平面镶嵌(或用多边形覆盖平面)。地砖与地砖之间无空隙。地砖与地砖之间不重叠。地砖把平面的一部分全部覆盖。正多边形镶嵌图案观察:1.镶嵌的正多边形的顶点、边长有什么特征?2、一个顶点处的各个正多边形的内角之和360°。正多边形镶嵌的条件:2.在一个顶点处的各内角和有什么关系?1、顶点公用,边长相等。探究1:仅用一种正多边形镶嵌,哪些能单独镶嵌成平面图案?第一组:用正三角形拼图
第二组:用正方形拼图
第三组:用正五边形拼图
第四组:用正六边形拼图
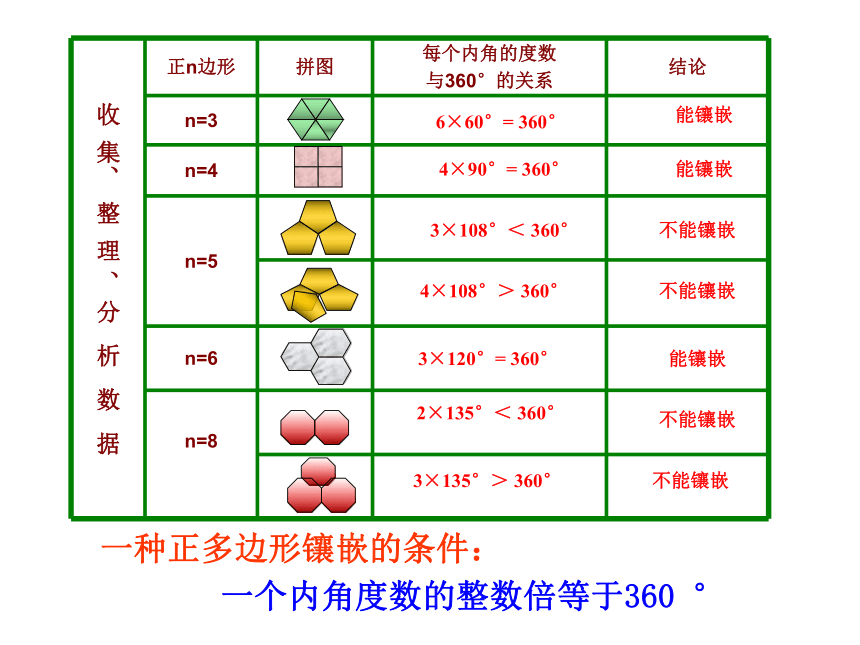
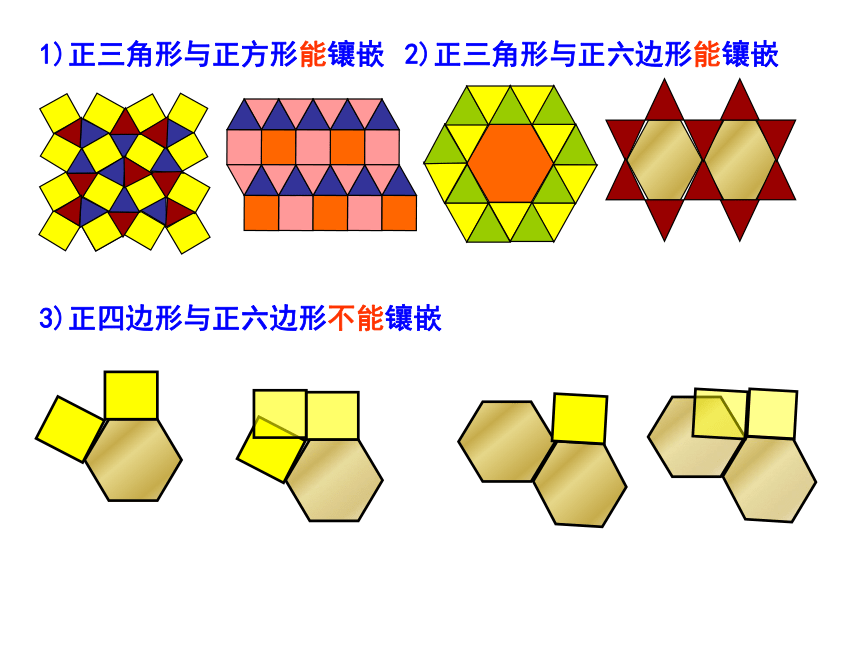
第五组:用正八边形拼图分组探究有空隙有重叠拼图过程能镶嵌不能镶嵌不能镶嵌能镶嵌6×60°= 360°4×90°= 360°4×108°> 360°3×120°= 360°3×108°< 360°能镶嵌2×135°< 360°不能镶嵌不能镶嵌3×135°> 360° 思考题:请用镶嵌条件 判断正七边形、正九边形能否镶嵌?归纳:用一种正多边形进行镶嵌,只有正三角形、正方形、正六边形能镶嵌成平面图案。探究2:小新搬新家了,他的房间要自己设计,地板想用两种正多边形来镶嵌,在建材市场买了正三角形、正方形、正六边形几种地板砖,请帮忙设计一个方案问题:用两种正多边形镶嵌,哪些能镶嵌成平面图案?1)正三角形与正方形能镶嵌 2)正三角形与正六边形能镶嵌3)正四边形与正六边形不能镶嵌1)为什么正三角形与正方形、正三角形与正六边形能镶嵌?60°×3 + 90°×2=360°60°×4 + 120°=360°60°×2 + 120°×2=360°2)为什么正方形和正六边形不能镶嵌?思 考 两种正多边形镶嵌的条件:拼接在一个顶点处的各个正多边形的内角和等于360° 探究3:
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
试一试。∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
结论:形状、大小相同的任意三角形能镶嵌成平面图案。因为∠1+∠2+∠3+∠4=360°所以形状、大小相同的任意四边形能镶嵌成平面图案。思考:为什么任意三角形、四边形能镶嵌成平面图案呢?任意三角形、四边形内角和的整数倍等于360°,所以能镶嵌成平面图案。(2003年中考题)商店出售下列形状的地砖:①正方形;②长方形; ③正五边形;④正六边形。若只选择其中某一种地砖镶嵌地面,可供选择的地砖共有( )
A.1种 B.2种 C.3种 D.4种边长为a的正方形与下列边长为a的正多边形组合起来,不能镶嵌成平面的是( )
①正三角形;②正五边形;③正六边形;④正八边形
A. ① ② B. ② ③ C. ① ③ D. ① ④CB课堂练习: 谈一谈:通过本课的学习有哪些收获和体会?欣赏不同的组合方式:
第二组:用正方形拼图
第三组:用正五边形拼图
第四组:用正六边形拼图
第五组:用正八边形拼图分组探究有空隙有重叠拼图过程能镶嵌不能镶嵌不能镶嵌能镶嵌6×60°= 360°4×90°= 360°4×108°> 360°3×120°= 360°3×108°< 360°能镶嵌2×135°< 360°不能镶嵌不能镶嵌3×135°> 360° 思考题:请用镶嵌条件 判断正七边形、正九边形能否镶嵌?归纳:用一种正多边形进行镶嵌,只有正三角形、正方形、正六边形能镶嵌成平面图案。探究2:小新搬新家了,他的房间要自己设计,地板想用两种正多边形来镶嵌,在建材市场买了正三角形、正方形、正六边形几种地板砖,请帮忙设计一个方案问题:用两种正多边形镶嵌,哪些能镶嵌成平面图案?1)正三角形与正方形能镶嵌 2)正三角形与正六边形能镶嵌3)正四边形与正六边形不能镶嵌1)为什么正三角形与正方形、正三角形与正六边形能镶嵌?60°×3 + 90°×2=360°60°×4 + 120°=360°60°×2 + 120°×2=360°2)为什么正方形和正六边形不能镶嵌?思 考 两种正多边形镶嵌的条件:拼接在一个顶点处的各个正多边形的内角和等于360° 探究3:
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
试一试。∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
结论:形状、大小相同的任意三角形能镶嵌成平面图案。因为∠1+∠2+∠3+∠4=360°所以形状、大小相同的任意四边形能镶嵌成平面图案。思考:为什么任意三角形、四边形能镶嵌成平面图案呢?任意三角形、四边形内角和的整数倍等于360°,所以能镶嵌成平面图案。(2003年中考题)商店出售下列形状的地砖:①正方形;②长方形; ③正五边形;④正六边形。若只选择其中某一种地砖镶嵌地面,可供选择的地砖共有( )
A.1种 B.2种 C.3种 D.4种边长为a的正方形与下列边长为a的正多边形组合起来,不能镶嵌成平面的是( )
①正三角形;②正五边形;③正六边形;④正八边形
A. ① ② B. ② ③ C. ① ③ D. ① ④CB课堂练习: 谈一谈:通过本课的学习有哪些收获和体会?欣赏不同的组合方式:
