数学八年级上青岛版5.5三角形内角和定理课件1
文档属性
| 名称 | 数学八年级上青岛版5.5三角形内角和定理课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-26 00:00:00 | ||
图片预览





文档简介
课件28张PPT。
青岛版 《数学》八年级(上)5.5 三角形内角和定理预习检查1、三角形内角和定理及其推论1、2是什么?
2、什么叫做推论?推论能作为定理使用吗?
3、什么叫做辅助线?辅助线通常画成什么线?
三角形蓝和三角形红见面了,蓝炫耀的说:“我的体积比你大,所以我的内角和也比你大!”红不服气的说:“那可不好说噢,你自己量量看!”
蓝用量角器量了量自己的内角和,就不再说话了! 同学们,你们知道其中的道理吗?
问题1问题2.
内角三兄弟之争 在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起了……”“为什么?” 老二很纳闷。
同学们,你们知道其中的道理吗?学 习 目 标1、通过拼图验证三角形内角和。
2、能理解和掌握三角形内角和定理 的证明过程。
3、能灵活应用三角形内角和定理进行简单的计算和推理证明。
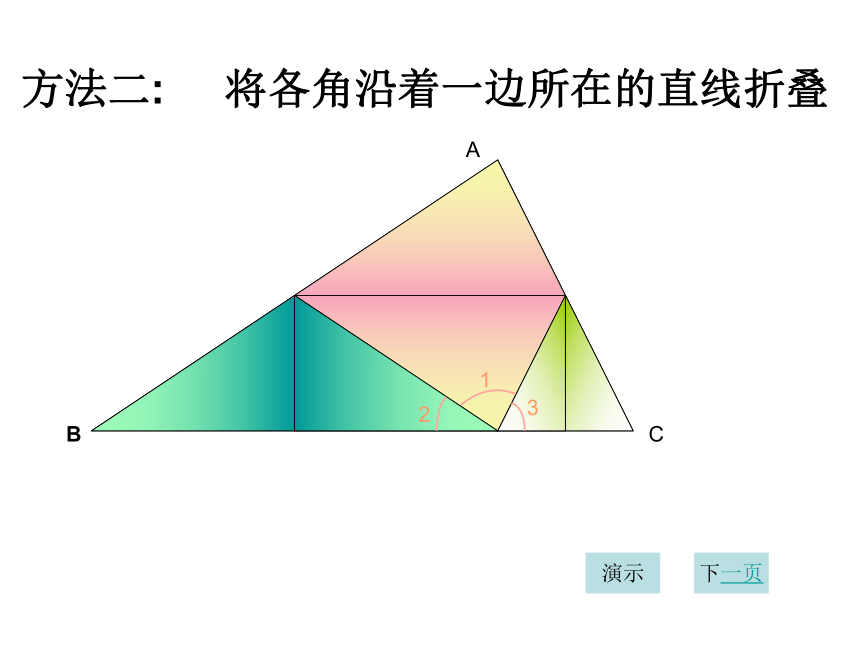
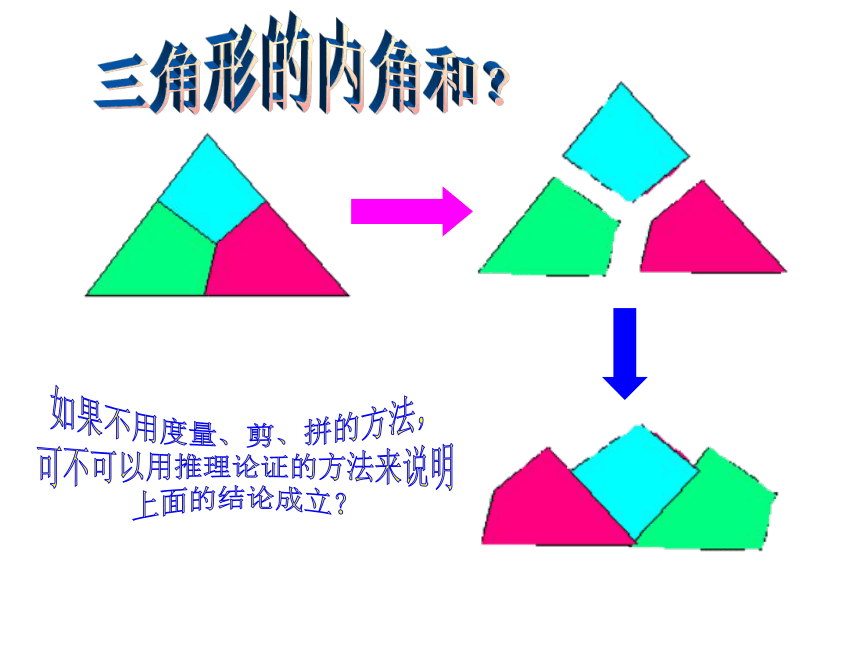
与三角形有关的角内角方法一: 度量演示下一页方法二: 将各角沿着一边所在的直线折叠三角形的内角和?如果不用度量、剪、拼的方法,
可不可以用推理论证的方法来说明
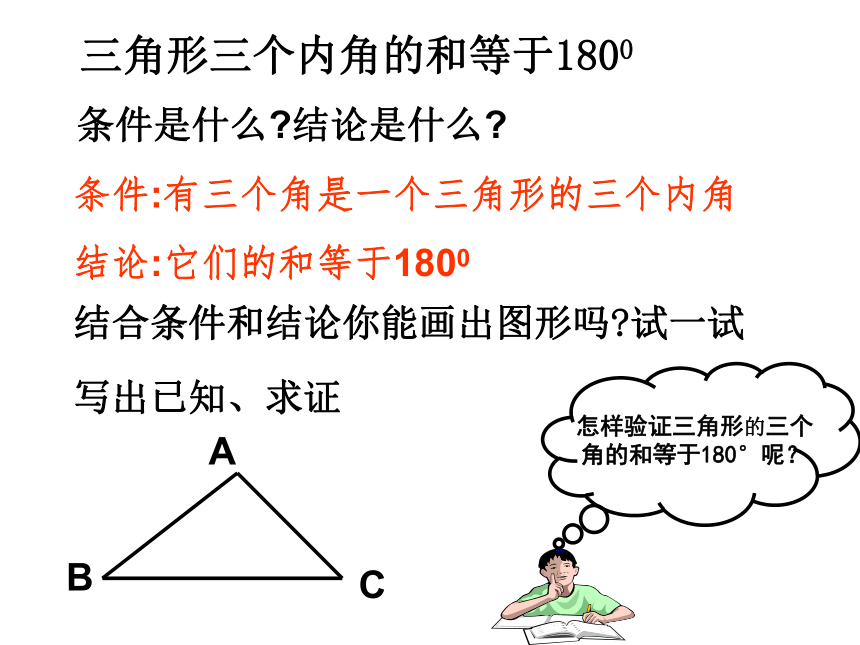
上面的结论成立?三角形三个内角的和等于1800条件:有三个角是一个三角形的三个内角
结论:它们的和等于1800结合条件和结论你能画出图形吗?试一试
写出已知、求证条件是什么?结论是什么?
想一想1.平角的度数是180°2.两直线平行,同旁内角的和是180° 从刚才拼角的过程你能想出证明的方法吗?3. 邻补角的和是180 °问题:有什么方法可以得到180°验证:三角形的三个内角和是180°图1图2ABCABC已知:如图,△ABC.
求证:∠A+∠B+∠C=1800.证明:作BC的延长线CD,过点C作∠A= ∠1,则 你还有其它方法来证明三角形内角
和定理吗?. CE∥AB( ) ∴ ∠2= ∠B( ). 又∵∠1+∠2+∠3=1800 ( ), ∴ ∠A+∠B+∠ACB=1800 ( ).分析:延长BC到D,过点C作∠A= ∠1,这样CE∥AB,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.这里的CD,CE称为辅助线,辅助线通常画成虚线.ABC已知:如图,△ABC.
求证:∠A+∠B+∠C=1800.证明:作BC的延长线CD,过点C作CE∥AB,则 ∠1=∠A( ) ∠2= ∠B( ). 又∵∠1+∠2+∠3=1800 ( ), ∴ ∠A+∠B+∠ACB=1800 ( ).分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.这里的CD,CE称为辅助线,辅助线通常画成虚线.ABCABCDE辅助线:在原来图形上添画的线叫辅助线.尝试一下:在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可以吗?小明的想法已经变为现实,由此你受到什么启发?你有新的证法吗?证明:过点A作PQ∥BC,则ABC ∠1=∠B( ), ∠2=∠C( ), 又∵∠1+∠2+∠3=1800 ( ), ∴ ∠BAC+∠B+∠C=1800 ( ).所作的辅助线是证明的一个重要组成部分,要在证明时首先叙述出来.2ABC证明:过A作AE∥BC,E提示:过D作DE∥AC, D F∥ABB三角形的内角和等于180°三角形的内角和定理:师生交流: 求出下列图中x的值: xx x x =600x x x =4502 x x┐x =300定理:三角形的三个内角和是180°一个三角形中能有两个直角吗?
一个三角形中能有两个钝角吗?
三个内角都能小于600吗?
讨论交流与发现由上图及三角形内角和定理,你还发现了什么?由此得出三角形内角和定理的两个推论:推论1:三角形的一个外角等于与它不相邻的两个内角的和。推论2:三角形的一个外角大于与它不相邻的任意一个内角。已知:如图,四边形ABCD是一个任意四边形。求证:∠A+∠B+ ∠C+ ∠D=36001.(1)在△ABC中,∠A=35°,∠ B=43°,
则∠ C= . (2)在△ABC中,∠C=90°,∠B=50°,
则∠A = ____。(3)在△ABC中, ∠A=40°,∠A=2∠B,
则∠C = ____。10204001200你真棒!当堂达标当堂达标2.已知△ABC中,∠B是∠A的2倍,
∠C比∠A大 ,求∠A .3.已知:三角形三个内角的度数之比为1:3:5,求这三个内角的度数。 解:设三个内角度数分别为:x、3x、5x,x+3x+5x=180°解得 x=20°所以三个内角度数分别为
20°,60°,100°。由三角形内角和为180°得当堂达标回顾与小结本节课里你学到了什么???1、知识点:
2、方法:⑴通过思考、去探究、去总结三角形内角和的 定理,并且发现要证明三角形三个内角的和等于180 °需通过作辅助线转化为:①平角;②两直线平行同旁内角和等于180°;③邻补角。(2)利用方程或方程组求角(3)把分散的角集中到三角形或多边形上。3、举一反三:
4、这一部分知识所在知识系统中的位置:
练习.如图,求?A1+?A2+?A3+?A4+?A5的度数。拓展延伸再见
青岛版 《数学》八年级(上)5.5 三角形内角和定理预习检查1、三角形内角和定理及其推论1、2是什么?
2、什么叫做推论?推论能作为定理使用吗?
3、什么叫做辅助线?辅助线通常画成什么线?
三角形蓝和三角形红见面了,蓝炫耀的说:“我的体积比你大,所以我的内角和也比你大!”红不服气的说:“那可不好说噢,你自己量量看!”
蓝用量角器量了量自己的内角和,就不再说话了! 同学们,你们知道其中的道理吗?
问题1问题2.
内角三兄弟之争 在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起了……”“为什么?” 老二很纳闷。
同学们,你们知道其中的道理吗?学 习 目 标1、通过拼图验证三角形内角和。
2、能理解和掌握三角形内角和定理 的证明过程。
3、能灵活应用三角形内角和定理进行简单的计算和推理证明。
与三角形有关的角内角方法一: 度量演示下一页方法二: 将各角沿着一边所在的直线折叠三角形的内角和?如果不用度量、剪、拼的方法,
可不可以用推理论证的方法来说明
上面的结论成立?三角形三个内角的和等于1800条件:有三个角是一个三角形的三个内角
结论:它们的和等于1800结合条件和结论你能画出图形吗?试一试
写出已知、求证条件是什么?结论是什么?
想一想1.平角的度数是180°2.两直线平行,同旁内角的和是180° 从刚才拼角的过程你能想出证明的方法吗?3. 邻补角的和是180 °问题:有什么方法可以得到180°验证:三角形的三个内角和是180°图1图2ABCABC已知:如图,△ABC.
求证:∠A+∠B+∠C=1800.证明:作BC的延长线CD,过点C作∠A= ∠1,则 你还有其它方法来证明三角形内角
和定理吗?. CE∥AB( ) ∴ ∠2= ∠B( ). 又∵∠1+∠2+∠3=1800 ( ), ∴ ∠A+∠B+∠ACB=1800 ( ).分析:延长BC到D,过点C作∠A= ∠1,这样CE∥AB,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.这里的CD,CE称为辅助线,辅助线通常画成虚线.ABC已知:如图,△ABC.
求证:∠A+∠B+∠C=1800.证明:作BC的延长线CD,过点C作CE∥AB,则 ∠1=∠A( ) ∠2= ∠B( ). 又∵∠1+∠2+∠3=1800 ( ), ∴ ∠A+∠B+∠ACB=1800 ( ).分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.这里的CD,CE称为辅助线,辅助线通常画成虚线.ABCABCDE辅助线:在原来图形上添画的线叫辅助线.尝试一下:在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可以吗?小明的想法已经变为现实,由此你受到什么启发?你有新的证法吗?证明:过点A作PQ∥BC,则ABC ∠1=∠B( ), ∠2=∠C( ), 又∵∠1+∠2+∠3=1800 ( ), ∴ ∠BAC+∠B+∠C=1800 ( ).所作的辅助线是证明的一个重要组成部分,要在证明时首先叙述出来.2ABC证明:过A作AE∥BC,E提示:过D作DE∥AC, D F∥ABB三角形的内角和等于180°三角形的内角和定理:师生交流: 求出下列图中x的值: xx x x =600x x x =4502 x x┐x =300定理:三角形的三个内角和是180°一个三角形中能有两个直角吗?
一个三角形中能有两个钝角吗?
三个内角都能小于600吗?
讨论交流与发现由上图及三角形内角和定理,你还发现了什么?由此得出三角形内角和定理的两个推论:推论1:三角形的一个外角等于与它不相邻的两个内角的和。推论2:三角形的一个外角大于与它不相邻的任意一个内角。已知:如图,四边形ABCD是一个任意四边形。求证:∠A+∠B+ ∠C+ ∠D=36001.(1)在△ABC中,∠A=35°,∠ B=43°,
则∠ C= . (2)在△ABC中,∠C=90°,∠B=50°,
则∠A = ____。(3)在△ABC中, ∠A=40°,∠A=2∠B,
则∠C = ____。10204001200你真棒!当堂达标当堂达标2.已知△ABC中,∠B是∠A的2倍,
∠C比∠A大 ,求∠A .3.已知:三角形三个内角的度数之比为1:3:5,求这三个内角的度数。 解:设三个内角度数分别为:x、3x、5x,x+3x+5x=180°解得 x=20°所以三个内角度数分别为
20°,60°,100°。由三角形内角和为180°得当堂达标回顾与小结本节课里你学到了什么???1、知识点:
2、方法:⑴通过思考、去探究、去总结三角形内角和的 定理,并且发现要证明三角形三个内角的和等于180 °需通过作辅助线转化为:①平角;②两直线平行同旁内角和等于180°;③邻补角。(2)利用方程或方程组求角(3)把分散的角集中到三角形或多边形上。3、举一反三:
4、这一部分知识所在知识系统中的位置:
练习.如图,求?A1+?A2+?A3+?A4+?A5的度数。拓展延伸再见
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
