数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系 课件(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系 课件(共23张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 779.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 19:38:08 | ||
图片预览






文档简介
(共23张PPT)
2.5.1 直线与圆的位置关系
第二章 直线和圆的方程
2.5 直线与圆、圆与圆的位置关系
高二数学备课组
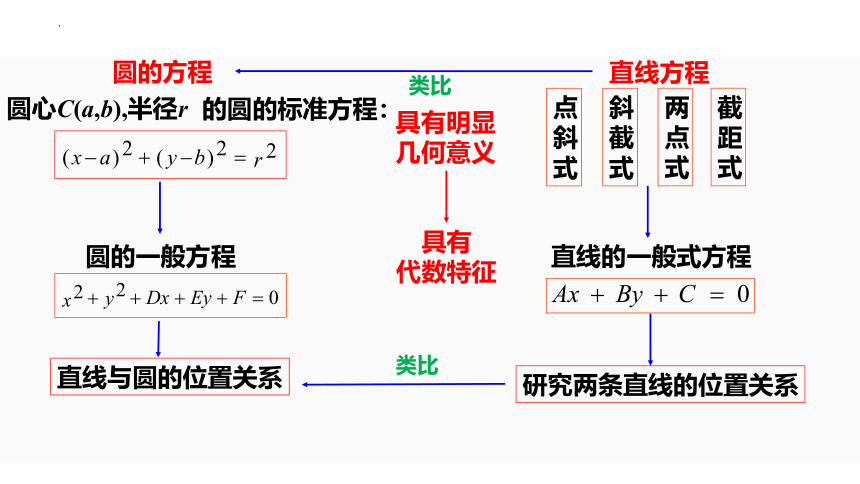
的圆的标准方程:
圆心C(a,b),半径r
圆的一般方程
具有
代数特征
直线方程
点斜式
斜
截
式
两
点式
截距式
具有明显几何意义
直线的一般式方程
圆的方程
研究两条直线的位置关系
类比
类比
直线与圆的位置关系
一、情景导入
“海上生明月,天涯共此时”,这是唐代诗人张九龄的诗句。
从这个景象中可以联想出哪些基本的几何图形呢?
它们有哪些位置关系呢?
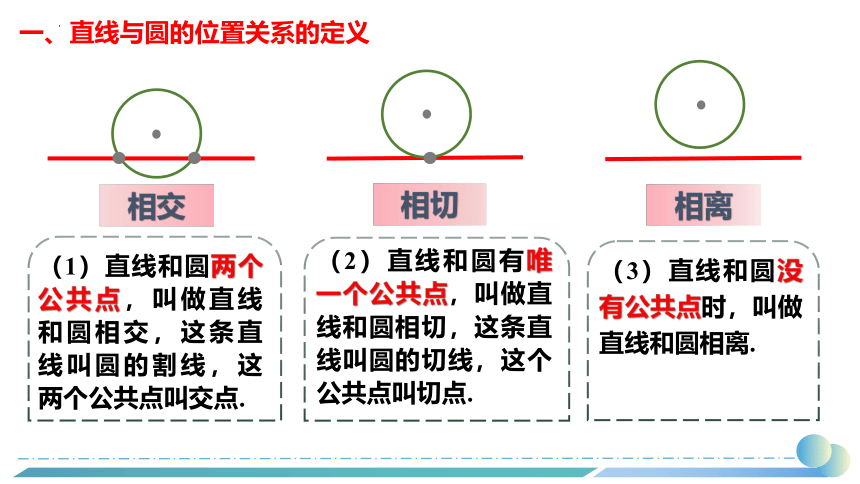
(1)直线和圆两个公共点,叫做直线和圆相交,这条直线叫圆的割线,这两个公共点叫交点.
相交
(2)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点.
相切
(3)直线和圆没有公共点时,叫做直线和圆相离.
相离
一、直线与圆的位置关系的定义
地平线
r
d
r
d
r
d
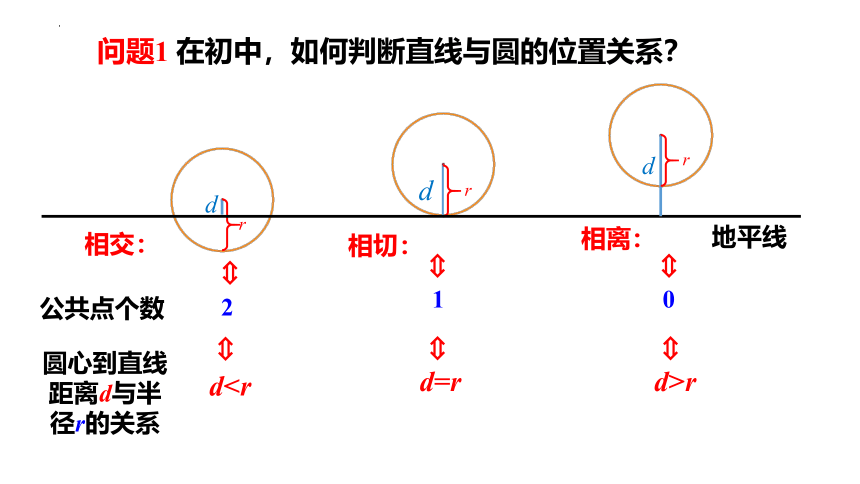
问题1 在初中,如何判断直线与圆的位置关系?
相交:
相切:
相离:
dd=r
d>r
公共点个数
圆心到直线距离d与半径r的关系
2
1
0
问题2 如何用直线的方程和圆的方程判断它们之间的位置关系?
例1 已知直线l: 3x+y-6=0和圆心为C的圆x2+y2-2y-4=0, (1)判断直线l与圆C的位置关系
例1 已知直线l: 3x+y-6=0和圆心为C的圆x2+y2-2y-4=0, 判断直线l与圆C的位置关系; 如果相交, 求直线l被圆C所截得的弦长.
解1:(代数法)
例1 已知直线l: 3x+y-6=0和圆心为C的圆x2+y2-2y-4=0, 判断直线l与圆C的位置关系; 如果相交, 求直线l被圆C所截得的弦长.
解2:(几何法)
x
O
y
6
2
1
B
A
d
l
C
二、直线与圆的位置关系的判定方法:
(1)(几何法)利用圆心到直线的距离d与半径r的大小关系判断:
直线l:Ax+By+C=0
圆C:(x-a)2+(y-b)2=r2(r>0)
d >r
相离
直线与圆
相交
(2) (代数法)利用直线与圆的公共点的个数进行判断:
n=0
n=1
n=2
相离
相切
相交
△<0
△=0
△>0
d=r
d相切
直线与圆
判定直线与圆的位置关系的方法:
(1)根据定义,可求出直线与圆的公共点的个数来判断;(代数法)
(2)根据性质,由圆心到直线的距离d与半径r的关系来判断。(几何法)
五、归纳总结
(3)直线x+2y-1=0和圆x2-2x+y2-y+1=0的位置关系为________
相交
1.(1)直线x+y-2=0与圆x2+y2=2的位置关系为________
相切
(2)直线x-y-2=0与圆(x-1)2+(y-1)2=1的位置关系为________
相离
2.直线 与圆x2+y2-2x-2=0相切,则实数m等于( )
C
3.若过点A(3,0)的直线l与圆(x-1)2+y2=1有公共点,则直线l的斜率可能是( )
BC
题型一 直线与圆的位置关系的判定
三、直线与圆相交时弦长的求法:
(1)几何法:用弦心距d,半径r及半弦构成直角三角形的三边.
垂径定理:垂直于弦的直径平分弦,且平分这条弦所对的两条弧.
由垂径定理,得
例1 已知直线l: 3x+y-6=0和圆心为C的圆x2+y2-2y-4=0, (1)判断直线l与圆C的位置关系
(2)如果相交, 求直线l被圆C所截得的弦长.
(2)代数法:计算出两交点
4. 已知直线l: y=x+1 和圆O: x2+y2=4 相交于A,B两点, 求弦长|AB|的值.
题型一 求直线与圆相交弦长
5. 已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0 所截得的弦长为8, 求直线l的方程.
解1:设圆心O(0,0)到直线的距离为d,则
x
y
O
A
B
d
r
4. 已知直线l: y=x+1 和圆O: x2+y2=4 相交于A,B两点,求弦长|AB|的值.
故弦长|AB|的值为 .
解2:
故弦长|AB|的值为 .
题型一 求直线与圆相交弦长
.
x
y
O
M
.
E
F
解:
由x2+y2+4y-21=0得,x2+(y+2)2=25,
则由
得
设所求直线方程:
即
解得 或
所求直线为
或
5. 已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0 所截得的弦长为8,求直线l的方程.
注意:首先要验证斜率不存在的情况.
4x+3y+21=0
x= -3
此时d=3,
∴不符合题意
当斜率不存在时,直线方程为x=-3,
∴圆心(0,-2),半径为5,
四、最长弦、最短弦问题
(1) 当l过圆心时,被圆截得的弦长最长,最长弦是直径,即为
(2) 当l与直径垂直时,被圆截得的弦长最短,即为
四、最长弦、最短弦问题
已知直线l过圆内一点
例3 (1)过点P(2, 1)作圆C: x2+y2=1的切线l, 求切线l的方程.
解:
-1
x
O
y
1
1
2
P(2,1)
r
分析:如图,点P(2,1)位于圆C:x2+y2=1外,经过圆外一点有两条直线与这个圆相切.我们设切线方程为y-1=k(x-2), k为斜率.由直线与圆相切可求出k的值.
例3(2)过圆x2+y2-2x-4y=0上一点P(3,3)的切线方程为
A.2x-y+9=0 B.2x+y-9=0
C.2x+y+9=0 D.2x-y-9=0
√
x2+y2-2x-4y=0的圆心为C(1,2),
∴切线方程为y-3=-2(x-3),即2x+y-9=0.
五、直线与圆相切问题:
先判断点P与圆C的位置关系
若点P在圆上,切线有一条
若点P在圆外,切线有两条
(1)点P在圆上时: 先求直线CP的斜率k,得切线的斜率为 ,由点斜式可得切线方程.如果斜率为零或不存在,则由图形可直接得切线方程 y=y0或 x=x0.
(2)点P在圆外时:
①斜率不存在时,x=x0,检验是否成立
②斜率存在时,设切线方程为y-y0=k(x-x0),由圆心到直线的距离等于半径,可求得k.
特别注意: 切线的斜率不存在的情况,不要漏解.
先定位,再定量
五、直线与圆相切问题:
例4由直线y=x+1上任一点向圆(x-3)2+y2=1引切线,则该切线长的最小值为( )
A.1 B. C. D.3
变式:已知P 是直线3x+4y+8=0上的动点,PA、PB 是圆(x-1)2+(y-1)2=1的两条切线,A、B 是切点,C 是圆心,则四边形PACB面积的最小值是( )
A. B.2 C. D.4
C
C
六、求切线长
如图,在圆C:(x-a)2+(y-b)2=r2外一点P(x0,y0)引圆的两条切线,切点分别为A,B,则
圆C:x2+y2+Dx+Ey+F=0
六、求切线长
判断直线和圆的位置关系的方法
弦长的求法
直线和圆的位置关系
定义
弦长公式法
几何法
代数法
几何法
代数法
直线与圆相切问题
相交
相切
相离
代数法
数形结合转化化归等
思想方法
2.5.1 直线与圆的位置关系
第二章 直线和圆的方程
2.5 直线与圆、圆与圆的位置关系
高二数学备课组
的圆的标准方程:
圆心C(a,b),半径r
圆的一般方程
具有
代数特征
直线方程
点斜式
斜
截
式
两
点式
截距式
具有明显几何意义
直线的一般式方程
圆的方程
研究两条直线的位置关系
类比
类比
直线与圆的位置关系
一、情景导入
“海上生明月,天涯共此时”,这是唐代诗人张九龄的诗句。
从这个景象中可以联想出哪些基本的几何图形呢?
它们有哪些位置关系呢?
(1)直线和圆两个公共点,叫做直线和圆相交,这条直线叫圆的割线,这两个公共点叫交点.
相交
(2)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点.
相切
(3)直线和圆没有公共点时,叫做直线和圆相离.
相离
一、直线与圆的位置关系的定义
地平线
r
d
r
d
r
d
问题1 在初中,如何判断直线与圆的位置关系?
相交:
相切:
相离:
d
d>r
公共点个数
圆心到直线距离d与半径r的关系
2
1
0
问题2 如何用直线的方程和圆的方程判断它们之间的位置关系?
例1 已知直线l: 3x+y-6=0和圆心为C的圆x2+y2-2y-4=0, (1)判断直线l与圆C的位置关系
例1 已知直线l: 3x+y-6=0和圆心为C的圆x2+y2-2y-4=0, 判断直线l与圆C的位置关系; 如果相交, 求直线l被圆C所截得的弦长.
解1:(代数法)
例1 已知直线l: 3x+y-6=0和圆心为C的圆x2+y2-2y-4=0, 判断直线l与圆C的位置关系; 如果相交, 求直线l被圆C所截得的弦长.
解2:(几何法)
x
O
y
6
2
1
B
A
d
l
C
二、直线与圆的位置关系的判定方法:
(1)(几何法)利用圆心到直线的距离d与半径r的大小关系判断:
直线l:Ax+By+C=0
圆C:(x-a)2+(y-b)2=r2(r>0)
d >r
相离
直线与圆
相交
(2) (代数法)利用直线与圆的公共点的个数进行判断:
n=0
n=1
n=2
相离
相切
相交
△<0
△=0
△>0
d=r
d
直线与圆
判定直线与圆的位置关系的方法:
(1)根据定义,可求出直线与圆的公共点的个数来判断;(代数法)
(2)根据性质,由圆心到直线的距离d与半径r的关系来判断。(几何法)
五、归纳总结
(3)直线x+2y-1=0和圆x2-2x+y2-y+1=0的位置关系为________
相交
1.(1)直线x+y-2=0与圆x2+y2=2的位置关系为________
相切
(2)直线x-y-2=0与圆(x-1)2+(y-1)2=1的位置关系为________
相离
2.直线 与圆x2+y2-2x-2=0相切,则实数m等于( )
C
3.若过点A(3,0)的直线l与圆(x-1)2+y2=1有公共点,则直线l的斜率可能是( )
BC
题型一 直线与圆的位置关系的判定
三、直线与圆相交时弦长的求法:
(1)几何法:用弦心距d,半径r及半弦构成直角三角形的三边.
垂径定理:垂直于弦的直径平分弦,且平分这条弦所对的两条弧.
由垂径定理,得
例1 已知直线l: 3x+y-6=0和圆心为C的圆x2+y2-2y-4=0, (1)判断直线l与圆C的位置关系
(2)如果相交, 求直线l被圆C所截得的弦长.
(2)代数法:计算出两交点
4. 已知直线l: y=x+1 和圆O: x2+y2=4 相交于A,B两点, 求弦长|AB|的值.
题型一 求直线与圆相交弦长
5. 已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0 所截得的弦长为8, 求直线l的方程.
解1:设圆心O(0,0)到直线的距离为d,则
x
y
O
A
B
d
r
4. 已知直线l: y=x+1 和圆O: x2+y2=4 相交于A,B两点,求弦长|AB|的值.
故弦长|AB|的值为 .
解2:
故弦长|AB|的值为 .
题型一 求直线与圆相交弦长
.
x
y
O
M
.
E
F
解:
由x2+y2+4y-21=0得,x2+(y+2)2=25,
则由
得
设所求直线方程:
即
解得 或
所求直线为
或
5. 已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0 所截得的弦长为8,求直线l的方程.
注意:首先要验证斜率不存在的情况.
4x+3y+21=0
x= -3
此时d=3,
∴不符合题意
当斜率不存在时,直线方程为x=-3,
∴圆心(0,-2),半径为5,
四、最长弦、最短弦问题
(1) 当l过圆心时,被圆截得的弦长最长,最长弦是直径,即为
(2) 当l与直径垂直时,被圆截得的弦长最短,即为
四、最长弦、最短弦问题
已知直线l过圆内一点
例3 (1)过点P(2, 1)作圆C: x2+y2=1的切线l, 求切线l的方程.
解:
-1
x
O
y
1
1
2
P(2,1)
r
分析:如图,点P(2,1)位于圆C:x2+y2=1外,经过圆外一点有两条直线与这个圆相切.我们设切线方程为y-1=k(x-2), k为斜率.由直线与圆相切可求出k的值.
例3(2)过圆x2+y2-2x-4y=0上一点P(3,3)的切线方程为
A.2x-y+9=0 B.2x+y-9=0
C.2x+y+9=0 D.2x-y-9=0
√
x2+y2-2x-4y=0的圆心为C(1,2),
∴切线方程为y-3=-2(x-3),即2x+y-9=0.
五、直线与圆相切问题:
先判断点P与圆C的位置关系
若点P在圆上,切线有一条
若点P在圆外,切线有两条
(1)点P在圆上时: 先求直线CP的斜率k,得切线的斜率为 ,由点斜式可得切线方程.如果斜率为零或不存在,则由图形可直接得切线方程 y=y0或 x=x0.
(2)点P在圆外时:
①斜率不存在时,x=x0,检验是否成立
②斜率存在时,设切线方程为y-y0=k(x-x0),由圆心到直线的距离等于半径,可求得k.
特别注意: 切线的斜率不存在的情况,不要漏解.
先定位,再定量
五、直线与圆相切问题:
例4由直线y=x+1上任一点向圆(x-3)2+y2=1引切线,则该切线长的最小值为( )
A.1 B. C. D.3
变式:已知P 是直线3x+4y+8=0上的动点,PA、PB 是圆(x-1)2+(y-1)2=1的两条切线,A、B 是切点,C 是圆心,则四边形PACB面积的最小值是( )
A. B.2 C. D.4
C
C
六、求切线长
如图,在圆C:(x-a)2+(y-b)2=r2外一点P(x0,y0)引圆的两条切线,切点分别为A,B,则
圆C:x2+y2+Dx+Ey+F=0
六、求切线长
判断直线和圆的位置关系的方法
弦长的求法
直线和圆的位置关系
定义
弦长公式法
几何法
代数法
几何法
代数法
直线与圆相切问题
相交
相切
相离
代数法
数形结合转化化归等
思想方法
