浙江省舟山市2023-2024学年金衢山五校联盟九年级第一学期10月质量监测数学试题卷(含答案)
文档属性
| 名称 | 浙江省舟山市2023-2024学年金衢山五校联盟九年级第一学期10月质量监测数学试题卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 09:12:03 | ||
图片预览




文档简介
浙江省舟山市2023-2024学年金衢山五校联盟九年级第一学期10月质量监测数学试题卷
注意事项:
1.全卷满分120分,考试时间120分钟.试题卷共8页,有三大题,共24小题,
2.本次考试为闭卷考试,全卷答案必须做在答题卷上,做在试题卷上无效.
第I卷(选择题)
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不给分)
1.下列事件为必然事件的是( )
A.明天会下雪 B.口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球
C.开电视机,央视第一套节目正在播放新闻 D.购买一张彩票中奖一百万元
2.若是二次函数,则m的值是( )
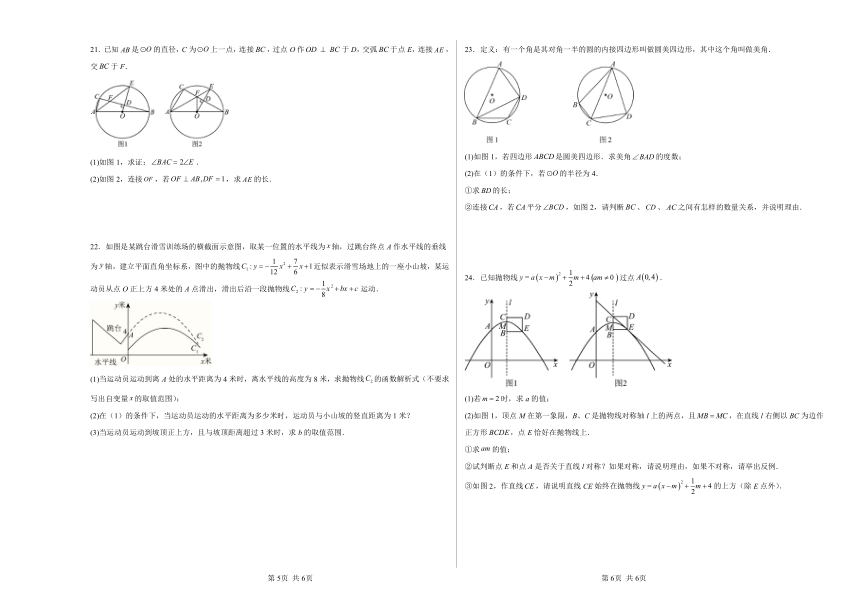
A.4 B.2 C. D. 或2
3.已知某二次函数上两点,,当时,;当时,,则该二次函数的解析式可以是( )
A. B. C. D.
4.如图,在平面直角坐标系中,,,,则外接圆的圆心坐标是( )
A. B. C. D.
5.在同一平面直角坐标系中,函数和函数(m是常数,且)的图象可能是( )
A. B. C. D.
6.如图所示,这个图案可以看作是以“基本图案”——原图案的四分之一通过变换形成的,但一定不能通过_________变换得到( )
A.旋转 B.轴对称 C.平移 D.轴对称和旋转
7.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x元后,每星期售出商品的总销售额为y元,则y与x的关系式为( )
A. B.
C. D.
8.如图1为某酒店的圆形旋转门,可看成如图2由外围的和3翼隔风玻璃组成,外围圆有通道和,且它们关于圆心中心对称,圆内的3翼隔风玻璃可绕圆心转动,且所成的夹角,3翼隔风玻璃在转动过程中,始终使大厅内外空气隔离,起到对大厅内保温作用.例如:当隔风玻璃转到如图2位置时,大厅内外空气被隔风玻璃,隔离.则通道所对圆心角的度数的最大值为( )
A.30° B.60° C.90° D.120°
9.如图,是圆O的直径,是弦,延长交的延长线于点A,连接,若,,则的度数是( )
A. B. C. D.
10.已知抛物线的顶点坐标为,若关于的一元二次方程(为实数)在范围内有两个不同的实数根,则实数的取值范围是( )
A. B. C. D.
第II卷(非选择题)
二 、填空题(本题有6小题,每小题4分,共24分)
11.如图,随机闭合开关,,中的两个,能够让灯泡发光的概率为 .
图11 图12
12.如图,点A,B,C,D,E都是上的点,,,则 .
13.已知二次函数,当时,函数值为;当时,函数值为,且,则时的函数值是
14.如图,已知,为线段上的一个动点,分别以,为边在的同侧作菱形和菱形,点,,在一条直线上,.,分别是对角线,的中点.当点在线段上移动时,点,之间的距离最短为 .
图14 图15
15.如图,边长为6的正方形的中心与半径为2的的圆心重合,过点O作,分别交、于点E、F,则图中阴影部分的面积为 .
16.已知点在二次函数,其中,,,,令,,,;为的个位数字为正整数,则下列说法:;;;的最小值为,此时;的个位数字为其中正确的是 填序号.
解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(1)解方程:. (2)计算:.
18.如图,是的弦,,,垂足分别为M、N,且.
(1)与相等吗?为什么?
(2)判断与是否相等,并说明理由.
19.在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 116 295 480 601
摸到白球的频率 a
(1)上表中的______;
(2)从袋中随机摸出一个球,“摸到白球”的概率的估计值是______(精确到);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的小球?
20.如图,二次函数的图象经过点且与轴交于点,点和点关于该二次函数图象的对称轴直线对称,一次函数的图象经过点及点.
(1)求二次函数与一次函数的解析式;
(2)根据图象,直接写出不等式的解集。
21.已知是的直径,C为上一点,连接,过点O作于D,交弧于点E,连接,交于F.
(1)如图1,求证:.
(2)如图2,连接,若,求的长.
22.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为轴,过跳台终点A作水平线的垂线为轴,建立平面直角坐标系,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿一段抛物线运动.
(1)当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线的函数解析式(不要求写出自变量的取值范围);
(2)在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?
(3)当运动员运动到坡顶正上方,且与坡顶距离超过3米时,求b的取值范围.
23.定义:有一个角是其对角一半的圆的内接四边形叫做圆美四边形,其中这个角叫做美角.
(1)如图1,若四边形是圆美四边形.求美角的度数;
(2)在(1)的条件下,若的半径为4.
①求的长;
②连接,若平分,如图2,请判断、、之间有怎样的数量关系,并说明理由.
24.已知抛物线过点.
(1)若时,求a的值;
(2)如图1,顶点M在第一象限,B、C是抛物线对称轴l上的两点,且,在直线l右侧以BC为边作正方形,点E恰好在抛物线上.
①求的值;
②试判断点E和点A是否关于直线l对称?如果对称,请说明理由,如果不对称,请举出反例.
③如图2,作直线,请说明直线CE始终在抛物线的上方(除E点外).
第1页 共4页 第2页 共4页
第1页 共4页 第2页 共4页
参考答案:
一、选择题(本题有10小题,每小题3分,共30分,请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B D A C A B D D
二、填空题(本题有6小题,共24分)
11. 12.116 13.5
14. 15. 16.
三、 解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
(1)(2)
18.【详解】(1)解:,理由如下:
∵,,
∴,
∵,
∴,即,
∴;
(2)解:,理由如下:
如图所示,连接,
在和中,
,
∴,
∴,
同理可证,
∴,
∴.
19.(1) (2) (3)8个
【详解】(1)解:;
(2)解:由表可知,当n很大时,摸到白球的频率将会接近,
∴“摸到白球”的概率的估计值是;
(3)解:个,
20.(1), (2)或
【详解】(1)二次函数的图象经过点,
,
二次函数图象的对称轴直线,
,
,,
二次函数的解析式为;
,
点和点关于该二次函数图象的对称轴直线对称,
,
设一次函数代解析式为,
,
,
一次函数的解析式为;
(2)由图象可得,不等式的解集或.
21.【详解】(1)证明:如图1中,
∵是直径,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴;
(2)解:如图2中,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
22.(1)抛物线的函数解析式为:
(2)运动员运动的水平距离为12米时,运动员与小山坡的竖直距离为1米
(3)
【详解】(1)由题意可知抛物线过点和,将其代入得:
,
解得,
∴抛物线的函数解析式为:;
(2)设运动员运动的水平距离为m米时,运动员与小山坡的竖直距离为1米,依题意得:
,
整理得:,
解得:,(舍去),
故运动员运动的水平距离为12米时,运动员与小山坡的竖直距离为1米;
(3),
当时,运动员到达坡顶,
即,
解得:.
23.【详解】(1)由题意得:,
,
,
.
(2)①如图1,连接并延长交于点,连接,
的半径为4,
,
,
.
②.
理由如下:如图2,延长到,使得,连接,
,
.
平分,
,.
,
,
,
,,
为等边三角形,
,
,
.
24.【详解】(1)解:∵,
∴二次函数表达式设为,
∵点在抛物线上,
∴,
∴;
(2)解:①∵抛物线过点,
∴,
∴,
∵,
∴,且,
∴;
②点E和点A关于直线l对称,理由如下:
∵抛物线的对称轴为,四边形为正方形,
∴,轴,
设,则,,
∴,
∴,,,
∵E恰好在抛物线上,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
又∵,对称轴为,
∴点E和点A关于直线l对称.
③,,
设直线的解析式为,
,
解得,,
∴直线的解析式为,
在x轴上取一点,过点G作直线轴,分别与直线,抛物线交于点K,H,
由题意知,,,,
则
.
当时,即时,,此时点E,H,K是同一个点;
当时,即时,,此时点K在点H的上方.
所以直线始终在抛物线上方(除E点外).
答案第1页,共2页
答案第1页,共2页
注意事项:
1.全卷满分120分,考试时间120分钟.试题卷共8页,有三大题,共24小题,
2.本次考试为闭卷考试,全卷答案必须做在答题卷上,做在试题卷上无效.
第I卷(选择题)
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不给分)
1.下列事件为必然事件的是( )
A.明天会下雪 B.口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球
C.开电视机,央视第一套节目正在播放新闻 D.购买一张彩票中奖一百万元
2.若是二次函数,则m的值是( )
A.4 B.2 C. D. 或2
3.已知某二次函数上两点,,当时,;当时,,则该二次函数的解析式可以是( )
A. B. C. D.
4.如图,在平面直角坐标系中,,,,则外接圆的圆心坐标是( )
A. B. C. D.
5.在同一平面直角坐标系中,函数和函数(m是常数,且)的图象可能是( )
A. B. C. D.
6.如图所示,这个图案可以看作是以“基本图案”——原图案的四分之一通过变换形成的,但一定不能通过_________变换得到( )
A.旋转 B.轴对称 C.平移 D.轴对称和旋转
7.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x元后,每星期售出商品的总销售额为y元,则y与x的关系式为( )
A. B.
C. D.
8.如图1为某酒店的圆形旋转门,可看成如图2由外围的和3翼隔风玻璃组成,外围圆有通道和,且它们关于圆心中心对称,圆内的3翼隔风玻璃可绕圆心转动,且所成的夹角,3翼隔风玻璃在转动过程中,始终使大厅内外空气隔离,起到对大厅内保温作用.例如:当隔风玻璃转到如图2位置时,大厅内外空气被隔风玻璃,隔离.则通道所对圆心角的度数的最大值为( )
A.30° B.60° C.90° D.120°
9.如图,是圆O的直径,是弦,延长交的延长线于点A,连接,若,,则的度数是( )
A. B. C. D.
10.已知抛物线的顶点坐标为,若关于的一元二次方程(为实数)在范围内有两个不同的实数根,则实数的取值范围是( )
A. B. C. D.
第II卷(非选择题)
二 、填空题(本题有6小题,每小题4分,共24分)
11.如图,随机闭合开关,,中的两个,能够让灯泡发光的概率为 .
图11 图12
12.如图,点A,B,C,D,E都是上的点,,,则 .
13.已知二次函数,当时,函数值为;当时,函数值为,且,则时的函数值是
14.如图,已知,为线段上的一个动点,分别以,为边在的同侧作菱形和菱形,点,,在一条直线上,.,分别是对角线,的中点.当点在线段上移动时,点,之间的距离最短为 .
图14 图15
15.如图,边长为6的正方形的中心与半径为2的的圆心重合,过点O作,分别交、于点E、F,则图中阴影部分的面积为 .
16.已知点在二次函数,其中,,,,令,,,;为的个位数字为正整数,则下列说法:;;;的最小值为,此时;的个位数字为其中正确的是 填序号.
解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(1)解方程:. (2)计算:.
18.如图,是的弦,,,垂足分别为M、N,且.
(1)与相等吗?为什么?
(2)判断与是否相等,并说明理由.
19.在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 116 295 480 601
摸到白球的频率 a
(1)上表中的______;
(2)从袋中随机摸出一个球,“摸到白球”的概率的估计值是______(精确到);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的小球?
20.如图,二次函数的图象经过点且与轴交于点,点和点关于该二次函数图象的对称轴直线对称,一次函数的图象经过点及点.
(1)求二次函数与一次函数的解析式;
(2)根据图象,直接写出不等式的解集。
21.已知是的直径,C为上一点,连接,过点O作于D,交弧于点E,连接,交于F.
(1)如图1,求证:.
(2)如图2,连接,若,求的长.
22.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为轴,过跳台终点A作水平线的垂线为轴,建立平面直角坐标系,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿一段抛物线运动.
(1)当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线的函数解析式(不要求写出自变量的取值范围);
(2)在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?
(3)当运动员运动到坡顶正上方,且与坡顶距离超过3米时,求b的取值范围.
23.定义:有一个角是其对角一半的圆的内接四边形叫做圆美四边形,其中这个角叫做美角.
(1)如图1,若四边形是圆美四边形.求美角的度数;
(2)在(1)的条件下,若的半径为4.
①求的长;
②连接,若平分,如图2,请判断、、之间有怎样的数量关系,并说明理由.
24.已知抛物线过点.
(1)若时,求a的值;
(2)如图1,顶点M在第一象限,B、C是抛物线对称轴l上的两点,且,在直线l右侧以BC为边作正方形,点E恰好在抛物线上.
①求的值;
②试判断点E和点A是否关于直线l对称?如果对称,请说明理由,如果不对称,请举出反例.
③如图2,作直线,请说明直线CE始终在抛物线的上方(除E点外).
第1页 共4页 第2页 共4页
第1页 共4页 第2页 共4页
参考答案:
一、选择题(本题有10小题,每小题3分,共30分,请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B D A C A B D D
二、填空题(本题有6小题,共24分)
11. 12.116 13.5
14. 15. 16.
三、 解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
(1)(2)
18.【详解】(1)解:,理由如下:
∵,,
∴,
∵,
∴,即,
∴;
(2)解:,理由如下:
如图所示,连接,
在和中,
,
∴,
∴,
同理可证,
∴,
∴.
19.(1) (2) (3)8个
【详解】(1)解:;
(2)解:由表可知,当n很大时,摸到白球的频率将会接近,
∴“摸到白球”的概率的估计值是;
(3)解:个,
20.(1), (2)或
【详解】(1)二次函数的图象经过点,
,
二次函数图象的对称轴直线,
,
,,
二次函数的解析式为;
,
点和点关于该二次函数图象的对称轴直线对称,
,
设一次函数代解析式为,
,
,
一次函数的解析式为;
(2)由图象可得,不等式的解集或.
21.【详解】(1)证明:如图1中,
∵是直径,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴;
(2)解:如图2中,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
22.(1)抛物线的函数解析式为:
(2)运动员运动的水平距离为12米时,运动员与小山坡的竖直距离为1米
(3)
【详解】(1)由题意可知抛物线过点和,将其代入得:
,
解得,
∴抛物线的函数解析式为:;
(2)设运动员运动的水平距离为m米时,运动员与小山坡的竖直距离为1米,依题意得:
,
整理得:,
解得:,(舍去),
故运动员运动的水平距离为12米时,运动员与小山坡的竖直距离为1米;
(3),
当时,运动员到达坡顶,
即,
解得:.
23.【详解】(1)由题意得:,
,
,
.
(2)①如图1,连接并延长交于点,连接,
的半径为4,
,
,
.
②.
理由如下:如图2,延长到,使得,连接,
,
.
平分,
,.
,
,
,
,,
为等边三角形,
,
,
.
24.【详解】(1)解:∵,
∴二次函数表达式设为,
∵点在抛物线上,
∴,
∴;
(2)解:①∵抛物线过点,
∴,
∴,
∵,
∴,且,
∴;
②点E和点A关于直线l对称,理由如下:
∵抛物线的对称轴为,四边形为正方形,
∴,轴,
设,则,,
∴,
∴,,,
∵E恰好在抛物线上,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
又∵,对称轴为,
∴点E和点A关于直线l对称.
③,,
设直线的解析式为,
,
解得,,
∴直线的解析式为,
在x轴上取一点,过点G作直线轴,分别与直线,抛物线交于点K,H,
由题意知,,,,
则
.
当时,即时,,此时点E,H,K是同一个点;
当时,即时,,此时点K在点H的上方.
所以直线始终在抛物线上方(除E点外).
答案第1页,共2页
答案第1页,共2页
同课章节目录
