数学八年级下青岛版6.2平行四边形的判定课件2
文档属性
| 名称 | 数学八年级下青岛版6.2平行四边形的判定课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 308.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-26 00:00:00 | ||
图片预览

文档简介
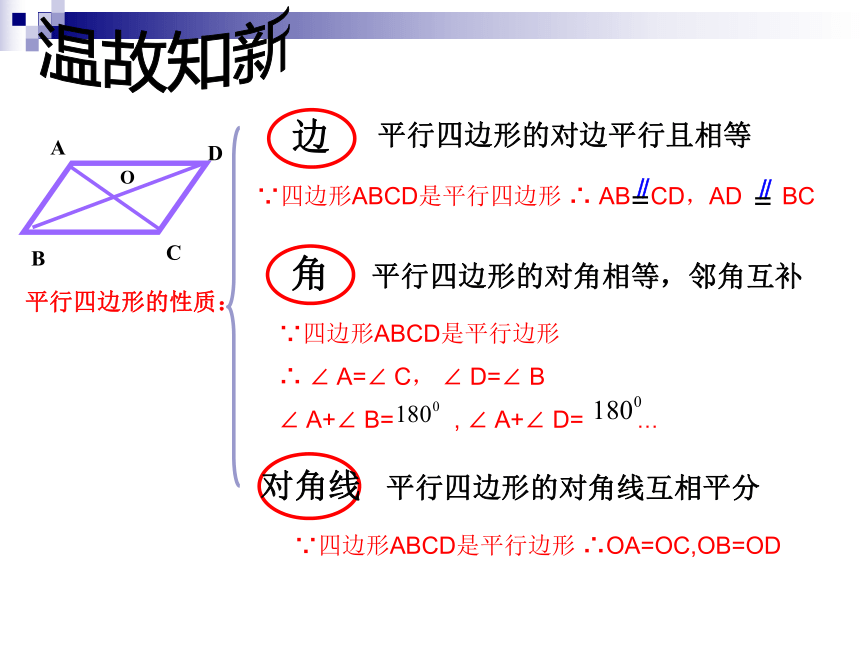
课件31张PPT。平行四边形的判定(一)平行四边形的对边平行且相等 平行四边形的对角线互相平分 温故知新平行四边形的性质:O平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
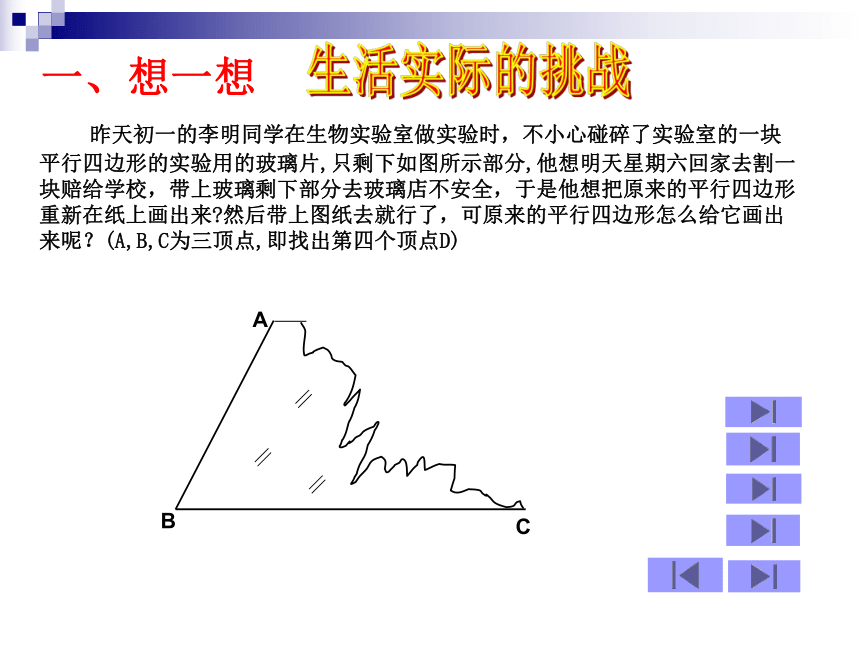
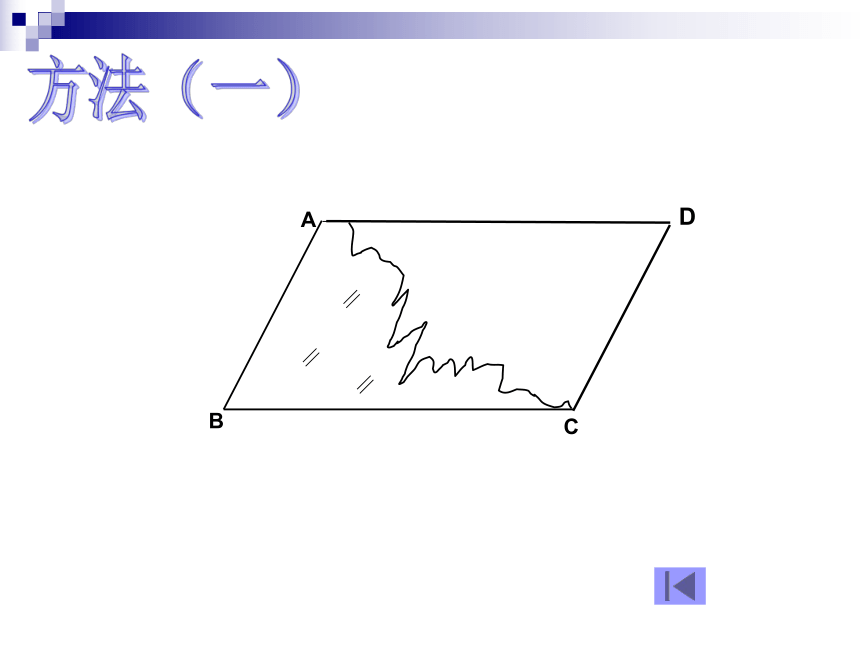
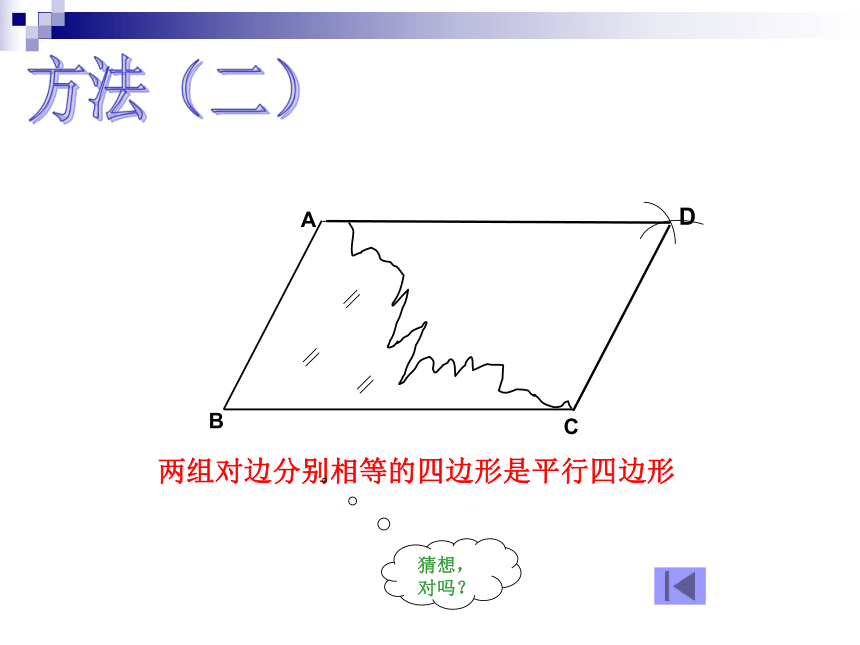
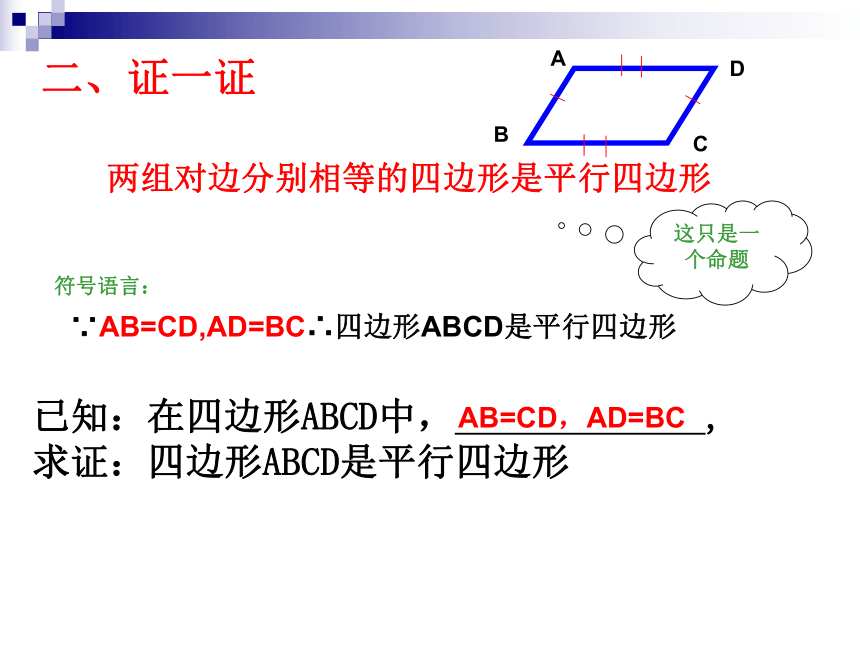
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD 昨天初一的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想明天星期六回家去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来?然后带上图纸去就行了,可原来的平行四边形怎么给它画出来呢?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战一、想一想方法(一)D方法(二)D两组对边分别相等的四边形是平行四边形猜想,对吗? 两组对边分别相等的四边形是平行四边形这只是一个命题∵AB=CD,AD=BC∴四边形ABCD是平行四边形已知:在四边形ABCD中, ,
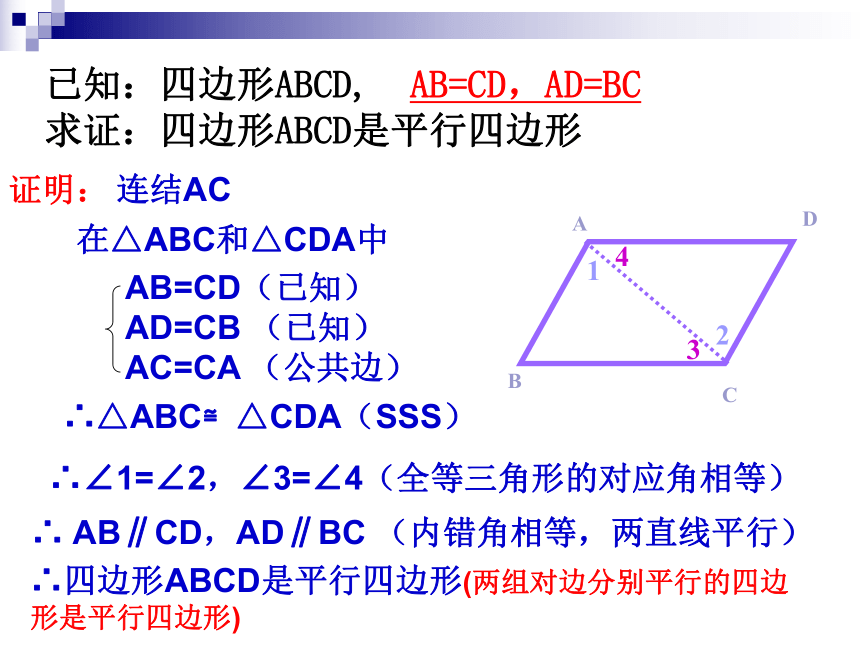
求证:四边形ABCD是平行四边形符号语言:AB=CD,AD=BC二、证一证已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC2134∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
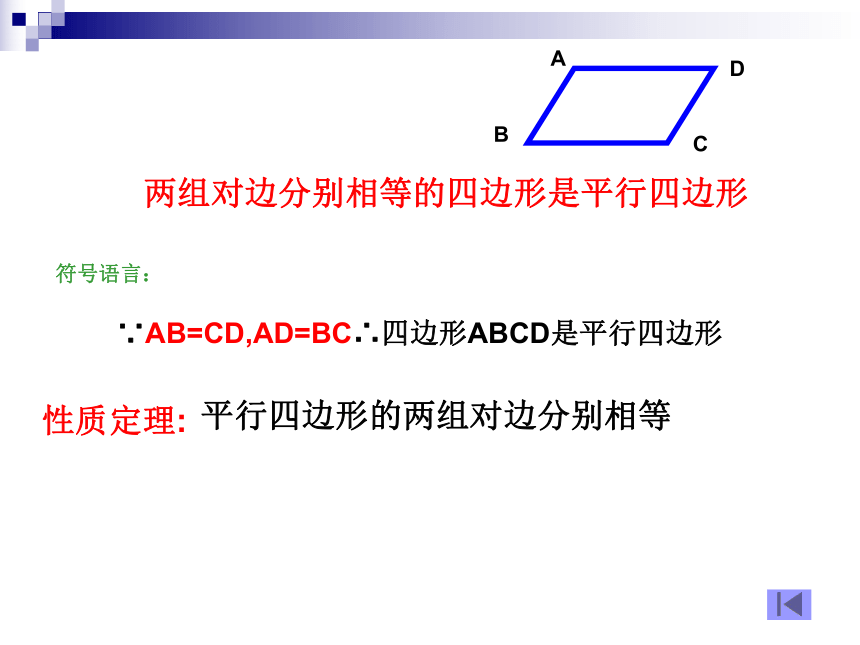
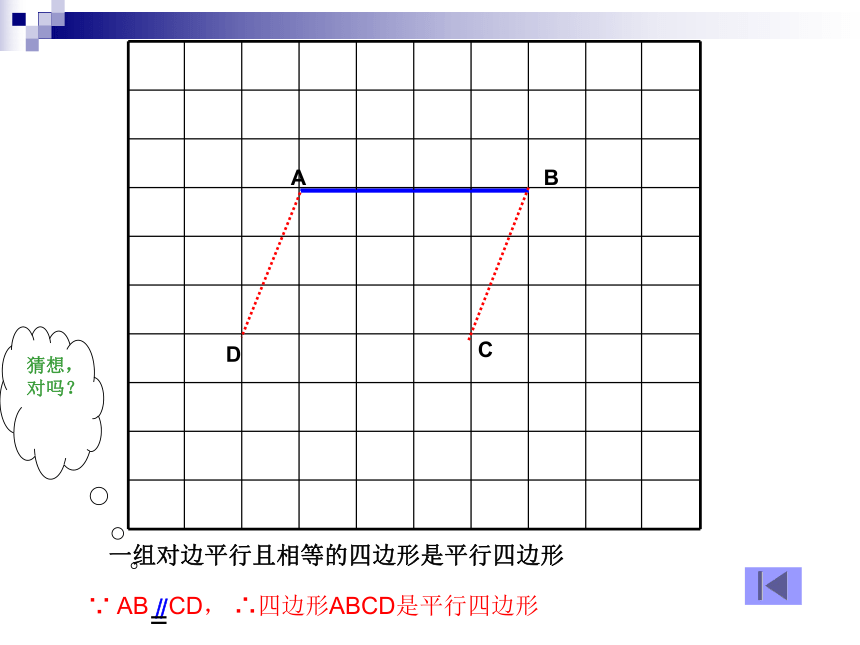
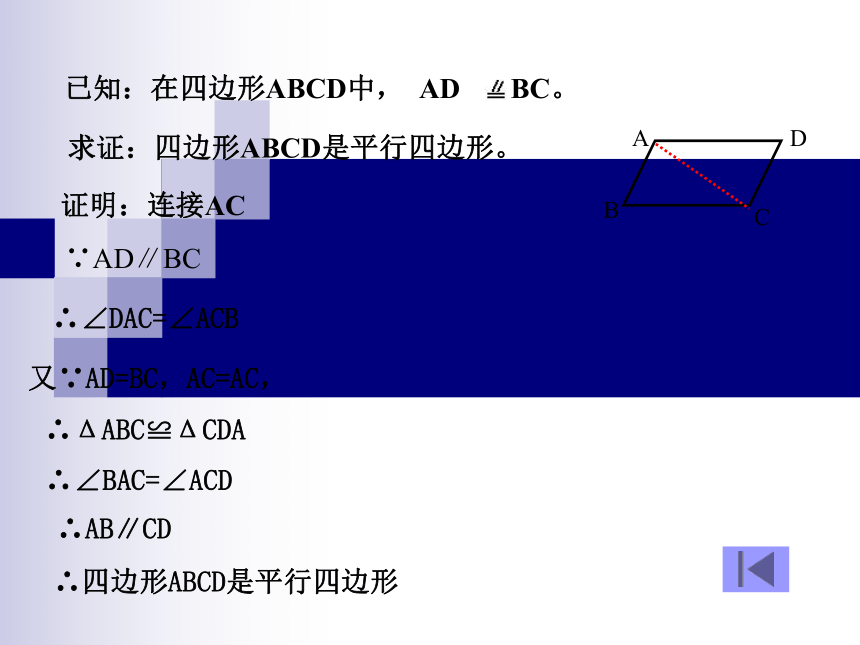
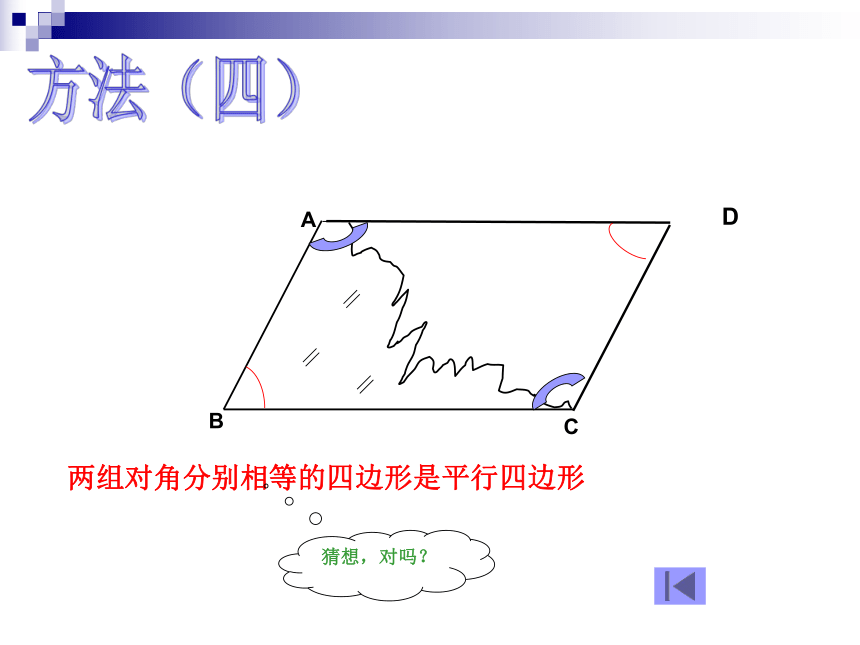
两组对边分别相等的四边形是平行四边形∵AB=CD,AD=BC∴四边形ABCD是平行四边形性质定理:符号语言: 平行四边形的两组对边分别相等方法(三)DCD一组对边平行且相等的四边形是平行四边形猜想,对吗?求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠DAC=∠ACB又∵AD=BC,AC=AC, ∴ΔABC≌ΔCDA∴∠BAC=∠ACD∴AB∥CD ∴四边形ABCD是平行四边形 已知:在四边形ABCD中, AD BC。方法(四)D两组对角分别相等的四边形是平行四边形猜想,对吗?方法(五)DO对角线互相平分的四边形是平行四边形猜想,对吗?O已知:四边形ABCD, 对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:在△AOD和△BOC中∴△ABC≌△CDA(SAS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
BAC2134三、猜一猜请写出下列性质定理的逆命题,并判断正确与否?你试一下吧!(4)平行四边形的两组对角分别相等逆命题:两组对角分别相等的四边形是平行四形(5)平行四边形的对角线互相平分逆命题:对角线互相平分四边形是平行四形符号语言:∵∠A=∠C,∠B=∠D ∴四边形ABCD是平行四边形符号语言:∵OA=OC,OB=OD ∴四边形ABCD是平行四边形(3)一组对边平行且相等的四边形是平行四边形符号语言:从边来判定1、两组对边分别平行的四边形是平行四边形(定义) 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形四、理一理平行四边形的判定方法 1、请你向同学们展示一下你的作品-----平行四边形,同时也向同学简要介绍一下你制作的过程,为什么你能确定你制作的四边形一定是平行四边形?理由是什么?五、试一试2、请你识别下列四边形哪些是平行四边形?为什么?⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝五、试一试 3、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)2、下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等,②一组对边相等且一条对角线平分另一条对角线,③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分,④一组对角相等,且这一组对角的顶点所连结的对角线平分这组对角。
A、①和② B、②和③
C、②和④ D、只有④D大显身手证明: 四边形ABCD是平行四边形AD ∥ BC且AD =BCEAD= FCBAE=CF
EAD= FCB
AD=BCAED ≌ CFB(SAS)DE=BF四边形BFDE是平行四边形在 AED和 CFB中同理可证:BE=DF4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形大显身手4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
5、如图,在 ?ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。画一画ADCBEFGHO六、说一说:
1.本节课你学会了几种平行四边形的判定方法2.本节课所学的解决问题的思路是: (2)碰到平行四边形的问题常转化为三角形来解决.(1)解决一个数学问题,常要通过”动手实践”-----”
猜想”-----”验证猜想(证明)”-----”得出结论”5.已知:如图,E,F分别是 的边AD,BC的中点。
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AB∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等),∵E,F分别是AD,BC的中点,∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。∴BE=DF(平行四边形的对边分别相等)。6.已知:如图,AB⊥AC,DC⊥AC,且AB=CD.
求证:AD∥CB.CBAD证明:∵AD⊥AC, BC⊥AC,∴AD∥BC, ∠BCA=∠DAC=90O,又∵AB=CD, AC=CA,∴Rt⊿ACB≌Rt⊿CAD.∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)。∴AB∥CD(平行四边形的定义)。1、如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?2、如图,E、F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.
求证:四边形ABCD是平行四边形.练习:4、如图, AC是□ABCD的一条对角线,
BM⊥AC, ND⊥AC,垂足分别是M、N .
求证:四边形BMDN是平行四边形.3、如图,O是□ABCD的对角线AC的中点,
过点O的直线EF分别交AB、CD于E、F两 点.
求证:四边形AECF是平行四边形.4.如图 四边形 ABCD和四边形BEDF都是平行四边形, 请你说明(1) AE=CF的理由
O变式:如图 已知 四边形 ABCD都是平行四边形, AE=CF,请你说明四边形BEDF是平行四边形
5、如图,在□ABCD中,延长AD到F,使
DF=AD,连结BF交CD于点E .
求证:点E平分CD与BF.
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD 昨天初一的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想明天星期六回家去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来?然后带上图纸去就行了,可原来的平行四边形怎么给它画出来呢?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战一、想一想方法(一)D方法(二)D两组对边分别相等的四边形是平行四边形猜想,对吗? 两组对边分别相等的四边形是平行四边形这只是一个命题∵AB=CD,AD=BC∴四边形ABCD是平行四边形已知:在四边形ABCD中, ,
求证:四边形ABCD是平行四边形符号语言:AB=CD,AD=BC二、证一证已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC2134∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
两组对边分别相等的四边形是平行四边形∵AB=CD,AD=BC∴四边形ABCD是平行四边形性质定理:符号语言: 平行四边形的两组对边分别相等方法(三)DCD一组对边平行且相等的四边形是平行四边形猜想,对吗?求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠DAC=∠ACB又∵AD=BC,AC=AC, ∴ΔABC≌ΔCDA∴∠BAC=∠ACD∴AB∥CD ∴四边形ABCD是平行四边形 已知:在四边形ABCD中, AD BC。方法(四)D两组对角分别相等的四边形是平行四边形猜想,对吗?方法(五)DO对角线互相平分的四边形是平行四边形猜想,对吗?O已知:四边形ABCD, 对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:在△AOD和△BOC中∴△ABC≌△CDA(SAS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
BAC2134三、猜一猜请写出下列性质定理的逆命题,并判断正确与否?你试一下吧!(4)平行四边形的两组对角分别相等逆命题:两组对角分别相等的四边形是平行四形(5)平行四边形的对角线互相平分逆命题:对角线互相平分四边形是平行四形符号语言:∵∠A=∠C,∠B=∠D ∴四边形ABCD是平行四边形符号语言:∵OA=OC,OB=OD ∴四边形ABCD是平行四边形(3)一组对边平行且相等的四边形是平行四边形符号语言:从边来判定1、两组对边分别平行的四边形是平行四边形(定义) 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形四、理一理平行四边形的判定方法 1、请你向同学们展示一下你的作品-----平行四边形,同时也向同学简要介绍一下你制作的过程,为什么你能确定你制作的四边形一定是平行四边形?理由是什么?五、试一试2、请你识别下列四边形哪些是平行四边形?为什么?⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝五、试一试 3、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)2、下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等,②一组对边相等且一条对角线平分另一条对角线,③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分,④一组对角相等,且这一组对角的顶点所连结的对角线平分这组对角。
A、①和② B、②和③
C、②和④ D、只有④D大显身手证明: 四边形ABCD是平行四边形AD ∥ BC且AD =BCEAD= FCBAE=CF
EAD= FCB
AD=BCAED ≌ CFB(SAS)DE=BF四边形BFDE是平行四边形在 AED和 CFB中同理可证:BE=DF4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形大显身手4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
5、如图,在 ?ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。画一画ADCBEFGHO六、说一说:
1.本节课你学会了几种平行四边形的判定方法2.本节课所学的解决问题的思路是: (2)碰到平行四边形的问题常转化为三角形来解决.(1)解决一个数学问题,常要通过”动手实践”-----”
猜想”-----”验证猜想(证明)”-----”得出结论”5.已知:如图,E,F分别是 的边AD,BC的中点。
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AB∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等),∵E,F分别是AD,BC的中点,∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。∴BE=DF(平行四边形的对边分别相等)。6.已知:如图,AB⊥AC,DC⊥AC,且AB=CD.
求证:AD∥CB.CBAD证明:∵AD⊥AC, BC⊥AC,∴AD∥BC, ∠BCA=∠DAC=90O,又∵AB=CD, AC=CA,∴Rt⊿ACB≌Rt⊿CAD.∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)。∴AB∥CD(平行四边形的定义)。1、如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?2、如图,E、F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.
求证:四边形ABCD是平行四边形.练习:4、如图, AC是□ABCD的一条对角线,
BM⊥AC, ND⊥AC,垂足分别是M、N .
求证:四边形BMDN是平行四边形.3、如图,O是□ABCD的对角线AC的中点,
过点O的直线EF分别交AB、CD于E、F两 点.
求证:四边形AECF是平行四边形.4.如图 四边形 ABCD和四边形BEDF都是平行四边形, 请你说明(1) AE=CF的理由
O变式:如图 已知 四边形 ABCD都是平行四边形, AE=CF,请你说明四边形BEDF是平行四边形
5、如图,在□ABCD中,延长AD到F,使
DF=AD,连结BF交CD于点E .
求证:点E平分CD与BF.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
