2023-2024学年北师大版七年级数学上册3.5 探究与表达规律 同步练习(无答案)
文档属性
| 名称 | 2023-2024学年北师大版七年级数学上册3.5 探究与表达规律 同步练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 491.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 08:25:51 | ||
图片预览



文档简介
3.5 探究与表达规律
核心知识盘点
等差数列
1,3,5,7,9,… ,2n-1
2,4,6,8,10,…,2n
1,4,7,10,13,… ,3n-2
平方数
1,4,9,16,25,…,
2,5,10,17,26,…,
0, 3, 8, 15,24,…,
4,9,16,25,…,
3,8,15,24,…,
立方数
1,8,27,64,125,…,
2,9,28,65,126,…,
8,27,64,125,216…,
7,26,63,124,215…,
等比数列
2,4,8,16,32,…,
1,3,7,15,31,…,
3,5,9,17,33,…,
裂项
2,6,12,20,30,…,n(n+1)
1,3,6,10,15,…,
4,12,24,40,60,...,2n(n+1)
斐波那契数列:
1,1,2,3,5,8,13,…,从第三个数开始每一个数等于与它相邻的前两个数的和.
正负交叉类
,,,,,,…,(为正整数).
,,,,,,…,(为正整数)
考点1:代数式中的变化规律
观察下列一组数:,则第n个数是
观察下列两行数:
0,2,4,6,8,10,12,14,16,…
0,3,6,9,12,15,18,21,24,…
探究发现:第1个相同的数是0,第2个相同的数是6,…,若第n个相同的数是102,则n等于
按一定规律排列的一列数依次为﹣1,2,﹣4,8,﹣16,32,…,第n个数是
一列数2,﹣5,10,﹣17,26,﹣37,…,按此规律排列下去,第n个数是
按规律排列的一组数,... ,则第2023个数是
观察下列一组数:,,,,,…,它们是按照一定规律排列的,那么这组数的第n个数是( )
A. B.(﹣1)n
C.(﹣1)n D.(﹣1)n﹣1
观察下列等式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,…,根据上述等式中的规律,则2+22+23+24+…+22023的末位数字是
考点2:数阵规律
将全体正整数排成一个三角形数阵:根据上述排列规律,数阵中第10行从左到右的第5个数是( )
A.48 B.49 C.50 D.51
观察如图中的数列排放顺序,根据其规律猜想:第10行第8个数应该是 .
将正整数按如图方式进行有规律的排列,第2行最后一个数是4,第3行最后一个数是7,第4行最后一个数是10,......,依此类推,请你判断2022所在的行数为( )
A.第672行 B.第673行 C.第674行 D.第675行
观察下面一列数:,,,,,,,将这列数排成下列形式:
按照上述规律排下去,那么第行从左边数第个数是 ;数是第 行从左边数第 个数.
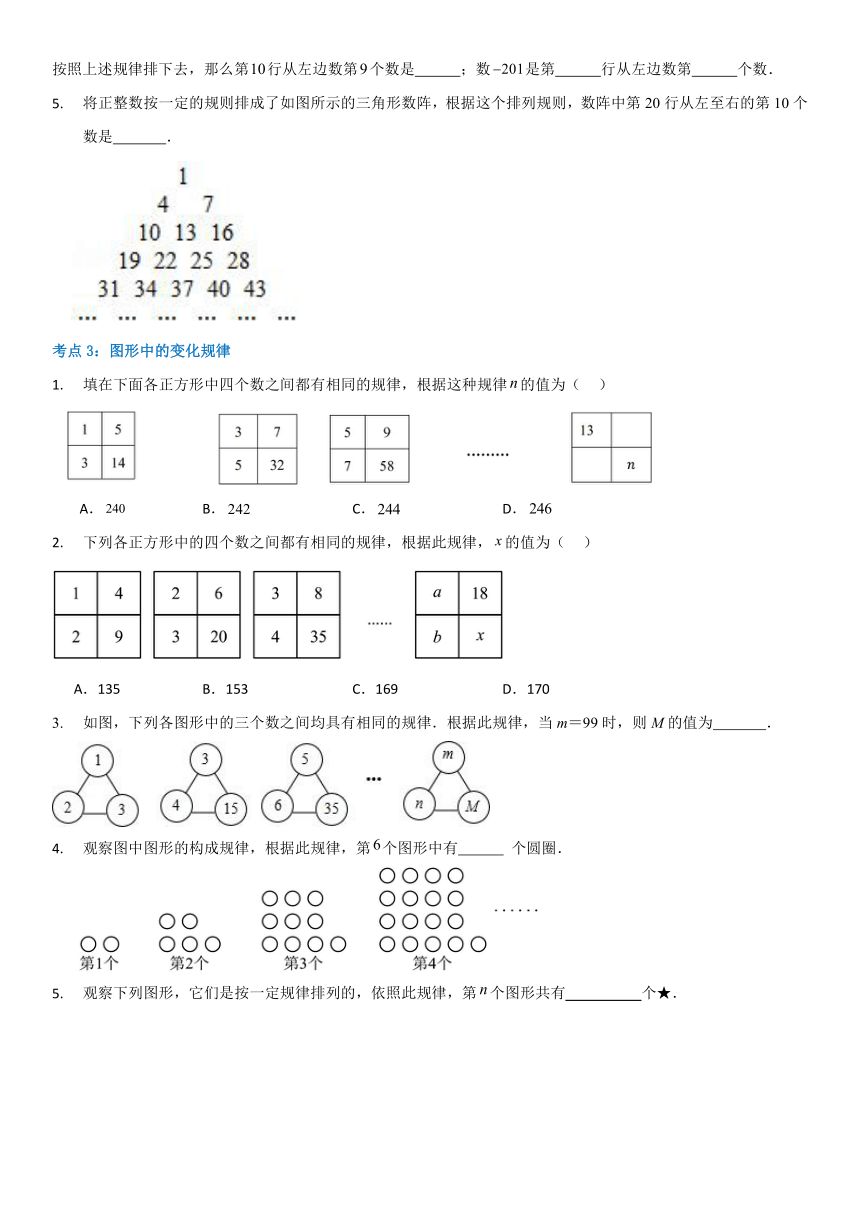
将正整数按一定的规则排成了如图所示的三角形数阵,根据这个排列规则,数阵中第20行从左至右的第10个数是 .
考点3:图形中的变化规律
填在下面各正方形中四个数之间都有相同的规律,根据这种规律的值为( )
A. B. C. D.
下列各正方形中的四个数之间都有相同的规律,根据此规律,的值为( )
A.135 B.153 C.169 D.170
如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,当m=99时,则M的值为 .
观察图中图形的构成规律,根据此规律,第个图形中有 个圆圈.
观察下列图形,它们是按一定规律排列的,依照此规律,第个图形共有 个★.
把黑色三角形按如图所示的规律拼图案,其中第1个图案中有1个黑色三角形,第2个图案中有3个黑色三角形,第3个图案中有6个黑色三角形,…,按此规律排列下去,则第7个图案中黑色三角形的个数为( )
A.20 B.25 C.28 D.30
我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为______.
下列小金鱼图案是用长度相同的小木棒按一定规律拼搭而成,第一条小金鱼图案需8根小木棒,第二条小金鱼图案需14根小木棒,…,按此规律,
(1)第n条小金鱼图案需要小木棒 根;
(2)如果有30000根小木棒,按照如图所示拼搭第1条,第2条……,直到第100条金鱼,请通过计算说明这些木棒是否够用.
如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,…,依此类推,则由正n边形“扩展”而来的多边形的边数为( ).
A.n(n-1) B.n(n+1) C.(n+1)(n-1) D.n2+2
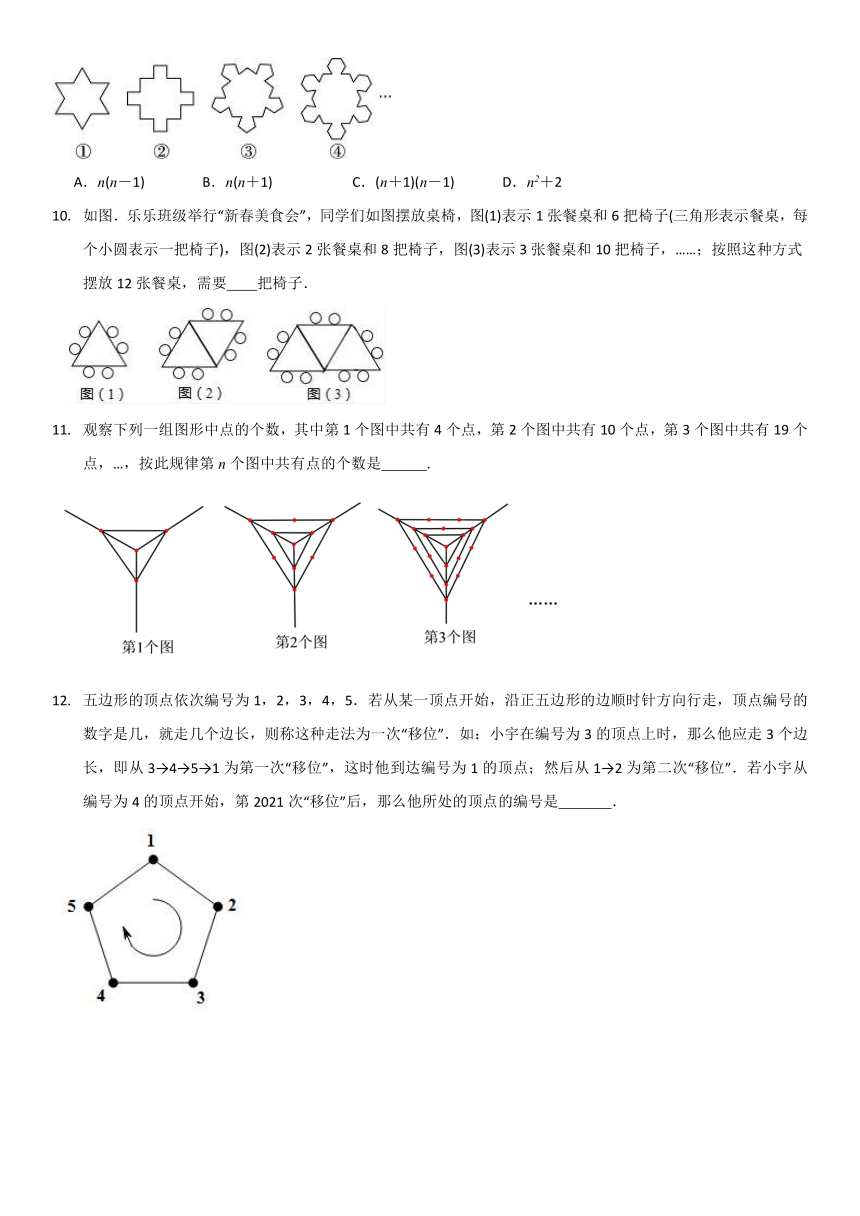
如图.乐乐班级举行“新春美食会”,同学们如图摆放桌椅,图(1)表示1张餐桌和6把椅子(三角形表示餐桌,每个小圆表示一把椅子),图(2)表示2张餐桌和8把椅子,图(3)表示3张餐桌和10把椅子,……;按照这种方式摆放12张餐桌,需要 把椅子.
观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第n个图中共有点的个数是 .
五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为4的顶点开始,第2021次“移位”后,那么他所处的顶点的编号是 .
如图所示,在一个电子青蛙游戏程序中,电子青蛙只能在标有五个数字点的圆周上跳动.游戏规则:若电子青蛙,停在奇数点上,则它下次沿顺时针方向跳两个点;若电子青蛙停在偶数点上,则它下次沿逆时针方向跳一个点.现在电子青蛙若从4这点开始跳,则经过次后它停的点对应的数为 .
考点4:日历中的变化规律
在日历表中,任意圈出一竖列上相邻的三个数,发现这三个数的和可能是( ).
A.18 B.40 C.60 D.75
小明计划和爸爸一起自驾游,图A是这月份的日历,用图B框住5个日期,他们的和是50,图B中x是出行日期,爸爸的车牌尾号是“9”,则出行日期是几号,这天能出行吗?( )(注:郑州市限行政策:周一到周五限行,周末和节假日不限行,每周一限行尾号为1和6,每周二限行尾号为2和7,以此类推)
图A:
周日 周一 周二 周三 周四 周五 周六
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
A.11,不能 B.11,能 C.10,能 D.10,不能
如图是由非负偶数排成的数阵:
(1)写出图中“H”形框中七个数的和与中间数的关系,
(2)在数阵中任意做一个这样的“H”形框,(1)中的关系仍然成立吗?并写出理由
(3)用这样的“H”形框能框出和为2023的七个数吗?如果能,求出七个数的中间数;如果不能,请写出理由.
如图,将连续的奇数1,3,5,7,按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数如图分别用a,b,c,d,x表示.
(1)计算:若十字框中间的数为17,则________;
(2)发现猜想:移动十字框,比较与中间的数x.则十字框中a、b、c、d的和是中间的数x的____倍;
(3)验证:用含x的式子分别表示出a、b、c、d,并利用整式运算验证(2)中猜想的正确性;
(4)应用:设,判断M的值能否等于2030,请说明理由.
如图,2021年3月的日历中有一个“M”形框,框中包含7个数.
(1)将“M”形框上下左右平移,但一定要框住2021年3月的日历中的7个数,若设“M”形框框住的7个数中,从小到大排第4个数为a,用含a的代数式表示“M”形框框住的7个数字之和;
(2)将“M”形框上下左右平移,“M”形框框住的7个数字之和能是133吗?如果能,请写出此时“M”形框中最小的数,如果不能,请说明理由.
实践与探索:将连续的奇数1,3,5,7…排列成如下的数表,用十字框框出5个数(如图).
(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a
的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于285吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于365吗?若能,分别写出十字框框住的5个数;若不能,请说明理由.
考点5:等式中的变化规律
观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
(4)求的值.
观察下列式子:
(1)请在理解上面计算方法的基础上,把下面两个数表示成两个分数的和的形式(分别写出表示的过程和结果)
=___________=___________;=___________=___________.
利用以上所得的规律进行计算:
阅读下列材料,完成相应任务:
神奇的等式
第1个等式:;
第2个等式:;
第3个等式:;第4个等式:;…
第100个等式:;…
任务:
(1)第6个等式为: ;
(2)猜想第n个等式: ;(用含n的代数式表示).
观察以下等式:
第1个等式:
第个等式:
第3个等式:
第个等式:
第5个等式:
······
按照以上规律.解决下列问题:
写出第个等式____________;
写出你猜想的第个等式:________________________(用含的等式表示).
观察下列式子:
1×3+1=22,2×4+1=32,3×5+1=42,4×6+1=52,…,
(1)请你依照上述规律,写出第6个式子: ;
(2)请写出第n个式子: ;
(3)计算:(1+)×(1+)×(1+)×…×(1+).
观察下列各式:
﹣1×=﹣1+
﹣×=﹣+
﹣×=﹣+
(1)你发现的规律是﹣×=_________.
(2)用规律计算:﹣1×+(﹣×)+(﹣× )+…+(﹣×)
阅读探究:;;;;…
(1)根据上述规律,求的值;
(2)你能用一个含有(为正整数)的算式表示这个规律吗?请直接写出这个算式(不计算);
(3)根据你发现的规律,计算下面算式的值:.
如图所示,将一个边长为1的正方形纸片分割成6个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,以此类推.
(1)图1的阴影部分的面积是 ;
(2)受此启发,得到++++的值是 ;
(3)若按这个方式继续分割下去,受前面问题的启发,可求得+++…+的值为 ;
(4)请你利用图2,再设计一个能求+++…+的值的几何图形.
【阅读】求值….
解:设S= …①
将等式①的两边同时乘以2得:2S= …②
由②﹣①得:
即:S= …
【运用】仿照此法计算:
(1)1+2+22+23+24+…+220
(2)1+5+52+53+54+…+5n(其中n为正整数).
【延伸】如图,将边长为1的正方形分成4个完全一样的小正方形,得到左上角一个小正方形为S1
,选取右下角的小正方形进行第二次操作,又得到左上角更小的正方形S2,依次操作2019次,依次得到小正方形S1、S2、S3、…、S2019.
完成下列问题:
(1)小正方形的面积S2019等于 ;
(2)求正方形S1、S2、S3、…、S2019的面积和.
为了求的值,可令,则,因此,所以.请仿照以上推理计算出的值是( )
A. B. C. D.
考点6:定义新运算
对于正整数n,定义f(n),例如:f(1),f(2),f(3),…,则f(1)+f(2)+f(3)+…+f(2022)+f(2023)的值为 .
定义一种对正整数n的“F运算”:①当n为奇数时,运算结果为3n+5;②当n为偶数时,结果为(其中k是使为奇数的正整数),并且运算重复进行,例如,取n=26,则
若n=898,则第2021次“F运算”的结果是( )
A.488 B.1 C.4 D.8
定义:a是不等于1的有理数,我们把称为a的差倒数.如3的差倒数是,﹣1的差倒数是,已知a2是a1的差倒数,a1=3,a3是a2的差倒数,a4是a3的差倒数,…以此类推,则a2020= .
考点7: 程序图
【例5】(温江区校级期末)如图所示的运算程序中,若开始输入的x值为24,我们发现第1次输出的结果为12,第2次输出的结果为6,…,则第2021次输出的结果为( )
A.6 B.3 C.24 D.12
【变式5-1】(晋安区期末)如图,是一个运算程序的示意图,若开始输入x的值为625,则第2020次输出的结果为( )
A.1 B.5 C.25 D.625
【变式5-2】(龙华区期末)如图是一个运算程序的示意图,若开始输入x的值为﹣2,则第2020次输出的结果为 .
【变式5-3】(新蔡县期末)按下面的程序计算:
若输入x=100,输出结果是501,若输入x=25,输出结果是631,若开始输入的x值为正整数,最后输出的结果为556,则开始输入的x值可能有( )
A.1种 B.2种 C.3种 D.4种
核心知识盘点
等差数列
1,3,5,7,9,… ,2n-1
2,4,6,8,10,…,2n
1,4,7,10,13,… ,3n-2
平方数
1,4,9,16,25,…,
2,5,10,17,26,…,
0, 3, 8, 15,24,…,
4,9,16,25,…,
3,8,15,24,…,
立方数
1,8,27,64,125,…,
2,9,28,65,126,…,
8,27,64,125,216…,
7,26,63,124,215…,
等比数列
2,4,8,16,32,…,
1,3,7,15,31,…,
3,5,9,17,33,…,
裂项
2,6,12,20,30,…,n(n+1)
1,3,6,10,15,…,
4,12,24,40,60,...,2n(n+1)
斐波那契数列:
1,1,2,3,5,8,13,…,从第三个数开始每一个数等于与它相邻的前两个数的和.
正负交叉类
,,,,,,…,(为正整数).
,,,,,,…,(为正整数)
考点1:代数式中的变化规律
观察下列一组数:,则第n个数是
观察下列两行数:
0,2,4,6,8,10,12,14,16,…
0,3,6,9,12,15,18,21,24,…
探究发现:第1个相同的数是0,第2个相同的数是6,…,若第n个相同的数是102,则n等于
按一定规律排列的一列数依次为﹣1,2,﹣4,8,﹣16,32,…,第n个数是
一列数2,﹣5,10,﹣17,26,﹣37,…,按此规律排列下去,第n个数是
按规律排列的一组数,... ,则第2023个数是
观察下列一组数:,,,,,…,它们是按照一定规律排列的,那么这组数的第n个数是( )
A. B.(﹣1)n
C.(﹣1)n D.(﹣1)n﹣1
观察下列等式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,…,根据上述等式中的规律,则2+22+23+24+…+22023的末位数字是
考点2:数阵规律
将全体正整数排成一个三角形数阵:根据上述排列规律,数阵中第10行从左到右的第5个数是( )
A.48 B.49 C.50 D.51
观察如图中的数列排放顺序,根据其规律猜想:第10行第8个数应该是 .
将正整数按如图方式进行有规律的排列,第2行最后一个数是4,第3行最后一个数是7,第4行最后一个数是10,......,依此类推,请你判断2022所在的行数为( )
A.第672行 B.第673行 C.第674行 D.第675行
观察下面一列数:,,,,,,,将这列数排成下列形式:
按照上述规律排下去,那么第行从左边数第个数是 ;数是第 行从左边数第 个数.
将正整数按一定的规则排成了如图所示的三角形数阵,根据这个排列规则,数阵中第20行从左至右的第10个数是 .
考点3:图形中的变化规律
填在下面各正方形中四个数之间都有相同的规律,根据这种规律的值为( )
A. B. C. D.
下列各正方形中的四个数之间都有相同的规律,根据此规律,的值为( )
A.135 B.153 C.169 D.170
如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,当m=99时,则M的值为 .
观察图中图形的构成规律,根据此规律,第个图形中有 个圆圈.
观察下列图形,它们是按一定规律排列的,依照此规律,第个图形共有 个★.
把黑色三角形按如图所示的规律拼图案,其中第1个图案中有1个黑色三角形,第2个图案中有3个黑色三角形,第3个图案中有6个黑色三角形,…,按此规律排列下去,则第7个图案中黑色三角形的个数为( )
A.20 B.25 C.28 D.30
我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为______.
下列小金鱼图案是用长度相同的小木棒按一定规律拼搭而成,第一条小金鱼图案需8根小木棒,第二条小金鱼图案需14根小木棒,…,按此规律,
(1)第n条小金鱼图案需要小木棒 根;
(2)如果有30000根小木棒,按照如图所示拼搭第1条,第2条……,直到第100条金鱼,请通过计算说明这些木棒是否够用.
如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,…,依此类推,则由正n边形“扩展”而来的多边形的边数为( ).
A.n(n-1) B.n(n+1) C.(n+1)(n-1) D.n2+2
如图.乐乐班级举行“新春美食会”,同学们如图摆放桌椅,图(1)表示1张餐桌和6把椅子(三角形表示餐桌,每个小圆表示一把椅子),图(2)表示2张餐桌和8把椅子,图(3)表示3张餐桌和10把椅子,……;按照这种方式摆放12张餐桌,需要 把椅子.
观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第n个图中共有点的个数是 .
五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为4的顶点开始,第2021次“移位”后,那么他所处的顶点的编号是 .
如图所示,在一个电子青蛙游戏程序中,电子青蛙只能在标有五个数字点的圆周上跳动.游戏规则:若电子青蛙,停在奇数点上,则它下次沿顺时针方向跳两个点;若电子青蛙停在偶数点上,则它下次沿逆时针方向跳一个点.现在电子青蛙若从4这点开始跳,则经过次后它停的点对应的数为 .
考点4:日历中的变化规律
在日历表中,任意圈出一竖列上相邻的三个数,发现这三个数的和可能是( ).
A.18 B.40 C.60 D.75
小明计划和爸爸一起自驾游,图A是这月份的日历,用图B框住5个日期,他们的和是50,图B中x是出行日期,爸爸的车牌尾号是“9”,则出行日期是几号,这天能出行吗?( )(注:郑州市限行政策:周一到周五限行,周末和节假日不限行,每周一限行尾号为1和6,每周二限行尾号为2和7,以此类推)
图A:
周日 周一 周二 周三 周四 周五 周六
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
A.11,不能 B.11,能 C.10,能 D.10,不能
如图是由非负偶数排成的数阵:
(1)写出图中“H”形框中七个数的和与中间数的关系,
(2)在数阵中任意做一个这样的“H”形框,(1)中的关系仍然成立吗?并写出理由
(3)用这样的“H”形框能框出和为2023的七个数吗?如果能,求出七个数的中间数;如果不能,请写出理由.
如图,将连续的奇数1,3,5,7,按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数如图分别用a,b,c,d,x表示.
(1)计算:若十字框中间的数为17,则________;
(2)发现猜想:移动十字框,比较与中间的数x.则十字框中a、b、c、d的和是中间的数x的____倍;
(3)验证:用含x的式子分别表示出a、b、c、d,并利用整式运算验证(2)中猜想的正确性;
(4)应用:设,判断M的值能否等于2030,请说明理由.
如图,2021年3月的日历中有一个“M”形框,框中包含7个数.
(1)将“M”形框上下左右平移,但一定要框住2021年3月的日历中的7个数,若设“M”形框框住的7个数中,从小到大排第4个数为a,用含a的代数式表示“M”形框框住的7个数字之和;
(2)将“M”形框上下左右平移,“M”形框框住的7个数字之和能是133吗?如果能,请写出此时“M”形框中最小的数,如果不能,请说明理由.
实践与探索:将连续的奇数1,3,5,7…排列成如下的数表,用十字框框出5个数(如图).
(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a
的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于285吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于365吗?若能,分别写出十字框框住的5个数;若不能,请说明理由.
考点5:等式中的变化规律
观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
(4)求的值.
观察下列式子:
(1)请在理解上面计算方法的基础上,把下面两个数表示成两个分数的和的形式(分别写出表示的过程和结果)
=___________=___________;=___________=___________.
利用以上所得的规律进行计算:
阅读下列材料,完成相应任务:
神奇的等式
第1个等式:;
第2个等式:;
第3个等式:;第4个等式:;…
第100个等式:;…
任务:
(1)第6个等式为: ;
(2)猜想第n个等式: ;(用含n的代数式表示).
观察以下等式:
第1个等式:
第个等式:
第3个等式:
第个等式:
第5个等式:
······
按照以上规律.解决下列问题:
写出第个等式____________;
写出你猜想的第个等式:________________________(用含的等式表示).
观察下列式子:
1×3+1=22,2×4+1=32,3×5+1=42,4×6+1=52,…,
(1)请你依照上述规律,写出第6个式子: ;
(2)请写出第n个式子: ;
(3)计算:(1+)×(1+)×(1+)×…×(1+).
观察下列各式:
﹣1×=﹣1+
﹣×=﹣+
﹣×=﹣+
(1)你发现的规律是﹣×=_________.
(2)用规律计算:﹣1×+(﹣×)+(﹣× )+…+(﹣×)
阅读探究:;;;;…
(1)根据上述规律,求的值;
(2)你能用一个含有(为正整数)的算式表示这个规律吗?请直接写出这个算式(不计算);
(3)根据你发现的规律,计算下面算式的值:.
如图所示,将一个边长为1的正方形纸片分割成6个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,以此类推.
(1)图1的阴影部分的面积是 ;
(2)受此启发,得到++++的值是 ;
(3)若按这个方式继续分割下去,受前面问题的启发,可求得+++…+的值为 ;
(4)请你利用图2,再设计一个能求+++…+的值的几何图形.
【阅读】求值….
解:设S= …①
将等式①的两边同时乘以2得:2S= …②
由②﹣①得:
即:S= …
【运用】仿照此法计算:
(1)1+2+22+23+24+…+220
(2)1+5+52+53+54+…+5n(其中n为正整数).
【延伸】如图,将边长为1的正方形分成4个完全一样的小正方形,得到左上角一个小正方形为S1
,选取右下角的小正方形进行第二次操作,又得到左上角更小的正方形S2,依次操作2019次,依次得到小正方形S1、S2、S3、…、S2019.
完成下列问题:
(1)小正方形的面积S2019等于 ;
(2)求正方形S1、S2、S3、…、S2019的面积和.
为了求的值,可令,则,因此,所以.请仿照以上推理计算出的值是( )
A. B. C. D.
考点6:定义新运算
对于正整数n,定义f(n),例如:f(1),f(2),f(3),…,则f(1)+f(2)+f(3)+…+f(2022)+f(2023)的值为 .
定义一种对正整数n的“F运算”:①当n为奇数时,运算结果为3n+5;②当n为偶数时,结果为(其中k是使为奇数的正整数),并且运算重复进行,例如,取n=26,则
若n=898,则第2021次“F运算”的结果是( )
A.488 B.1 C.4 D.8
定义:a是不等于1的有理数,我们把称为a的差倒数.如3的差倒数是,﹣1的差倒数是,已知a2是a1的差倒数,a1=3,a3是a2的差倒数,a4是a3的差倒数,…以此类推,则a2020= .
考点7: 程序图
【例5】(温江区校级期末)如图所示的运算程序中,若开始输入的x值为24,我们发现第1次输出的结果为12,第2次输出的结果为6,…,则第2021次输出的结果为( )
A.6 B.3 C.24 D.12
【变式5-1】(晋安区期末)如图,是一个运算程序的示意图,若开始输入x的值为625,则第2020次输出的结果为( )
A.1 B.5 C.25 D.625
【变式5-2】(龙华区期末)如图是一个运算程序的示意图,若开始输入x的值为﹣2,则第2020次输出的结果为 .
【变式5-3】(新蔡县期末)按下面的程序计算:
若输入x=100,输出结果是501,若输入x=25,输出结果是631,若开始输入的x值为正整数,最后输出的结果为556,则开始输入的x值可能有( )
A.1种 B.2种 C.3种 D.4种
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
