第二十三章 旋转 复习讲义(无答案) 2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十三章 旋转 复习讲义(无答案) 2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 275.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 11:26:51 | ||
图片预览


文档简介
旋转与中心对称
共同特点:如果把时针、风车风轮当成一个图形,那么这些图形都可以绕着 转动一定的角度.
像这样,把一个图形绕着某一点O转动一个角度的图形变换叫做 ,点O叫做 ,转动的角叫做 ;如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个 .
旋转的三个要素: , , .
◆对应点到旋转中心的距离 .
◆对应点与旋转中心所连线段的夹角等于 .
◆旋转前、后的图形 .
图形的旋转不改变图形的形状、大小,只改变图形的位置.
中心对称图形:
绕着中心点旋转180度后能与自身重合的图形叫做中心对称图形,这个中心点叫做对称中心.
当旋转角为180°时,旋转对称图形是一个中心对称图形,所以中心对称图形是旋转对称图形的特例.
中心对称:
把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
成中心对称的性质:
1.成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
2.成中心对称的两个图形,大小相等,形状相同,两个图形全等.
3.成中心对称的两个图形,对应线段平行(或在同一直线上)且相等.
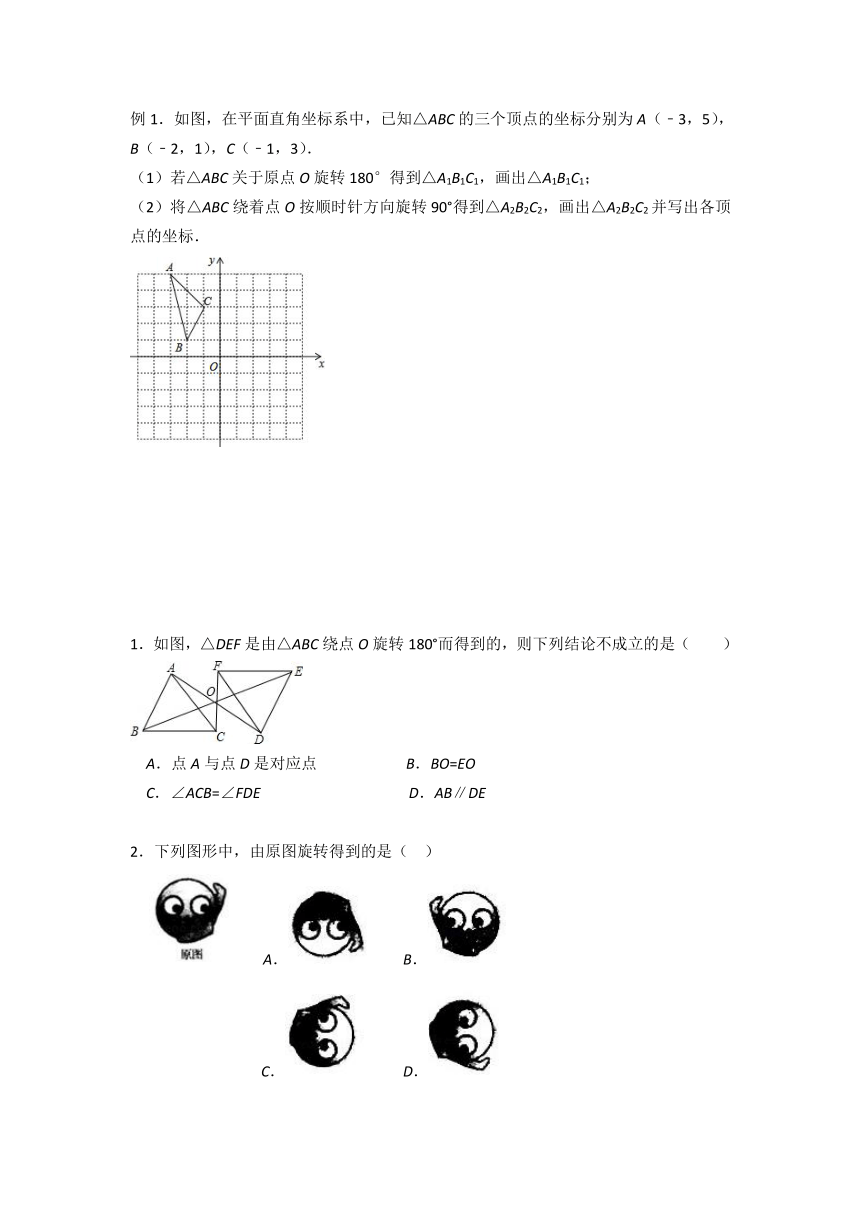
例1.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC关于原点O旋转180°得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕着点O按顺时针方向旋转90°得到△A2B2C2,画出△A2B2C2并写出各顶点的坐标.
1.如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )
A.点A与点D是对应点 B.BO=EO
C.∠ACB=∠FDE D.AB∥DE
2.下列图形中,由原图旋转得到的是( )
A. B.
C. D.
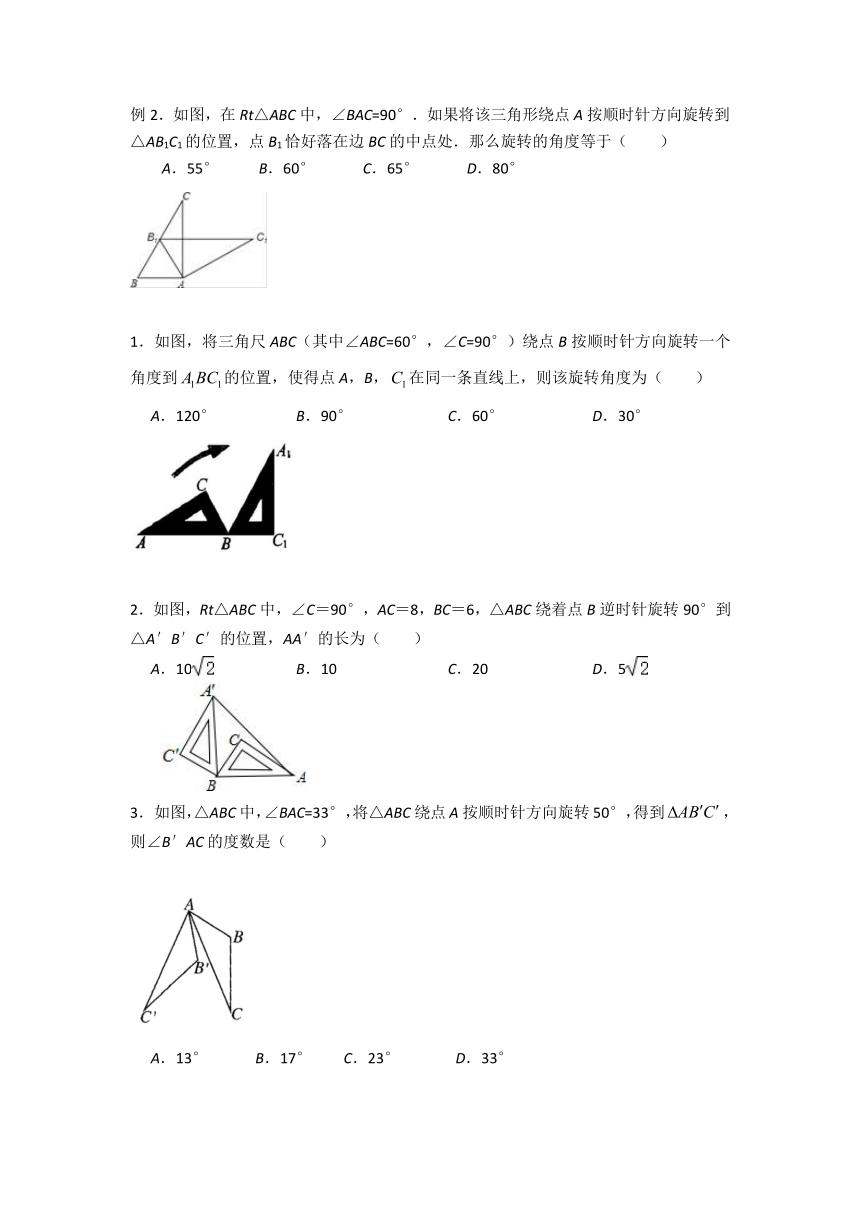
例2.如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于( )
A.55° B.60° C.65° D.80°
1.如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕点B按顺时针方向旋转一个角度到的位置,使得点A,B,在同一条直线上,则该旋转角度为( )
A.120° B.90° C.60° D.30°
2.如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
A.10 B.10 C.20 D.5
如图,△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,得到,则∠B′AC的度数是( )
A.13° B.17° C.23° D.33°
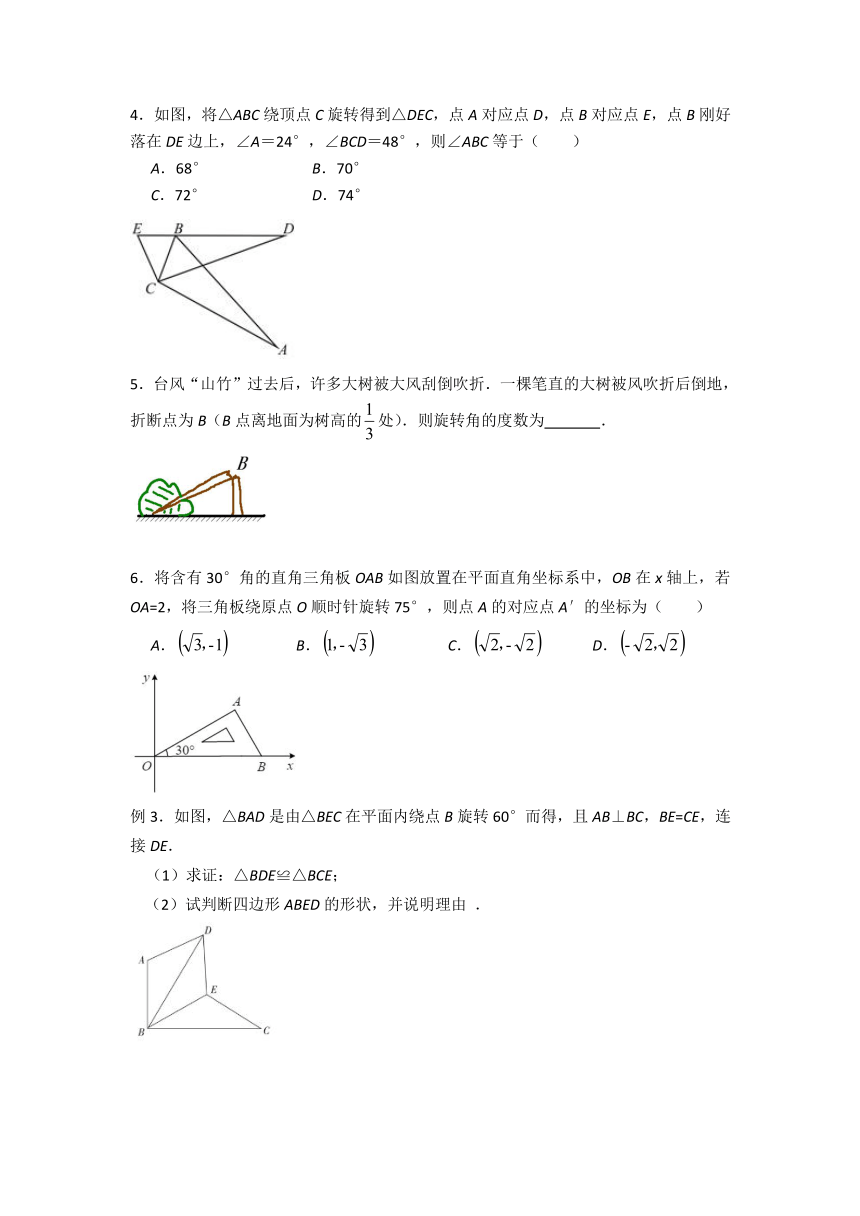
4.如图,将△ABC绕顶点C旋转得到△DEC,点A对应点D,点B对应点E,点B刚好落在DE边上,∠A=24°,∠BCD=48°,则∠ABC等于( )
A.68° B.70°
C.72° D.74°
5.台风“山竹”过去后,许多大树被大风刮倒吹折.一棵笔直的大树被风吹折后倒地,折断点为B(B点离地面为树高的处).则旋转角的度数为 .
6.将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
A. B. C. D.
例3.如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
求证:△BDE≌△BCE;
试判断四边形ABED的形状,并说明理由 .
1.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE.
(1)求证:∠A=∠EBC;
(2)若已知旋转角为40°,∠ACE=140°,求∠CED和∠BDE的度数.
例4.在线段,等腰梯形,平行四边形,矩形,正五角星,圆,正方形,等边三角形中,既是轴对称图形,又是中心对称图形的图形有( )
A.3个 B.4个 C.5个 D.6个
1.下列四个图案中,不是中心对称图形的是( )
A. B. C. D.
2.下列平面图形中,既是中心对称图形,又是轴对称图形的是( )
A.菱形 B.等边三角形 C.平行四边形 D.等腰梯形
3.(1)点P (a,b)关于原点对称的点的坐标( )
(2)点P (a,b)关于x轴对称的点的坐标( )
(3)点P (a,b)关于y轴对称的点的坐标( )
例5.如图,△BCM中,∠BMC=120°,以BC为边向三角形外作等边△ABC,把△ABM绕着点A按逆时针方向旋转60°到△CAN的位置.若BM=2,MC=3.
求:①∠AMB的度数;②求AM的长.
1.已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.
例6.如图,在正方形ABCD中,E是边AD上一点,将△ABE绕点A按逆时针方向旋转90°到△ADF的位置.已知AF=5,BE=13.
(1)求DE的长度;
(2)BE与DF是否垂直?说明你的理由.
1.如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是 .
2.如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D按逆时针方向旋转90°得到△DCM.
(1)求证:EF=MF;
(2)当AE=1时,求EF的长.
例7.如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.
(1)图中△EFD可以由 绕点 旋转 后得到;
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
1.如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想线段AE与BF的长短有何关系?说明理由;
(2)若△ABC的面积为3cm2,求四边形ABFE的面积;
(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由.
例8.如图,在平面直角坐标系中,等腰Rt△OA1B1的斜边OA1=2,且OA1在x轴的正半轴上,点B1落在第一象限内.将Rt△OA1B1绕原点O逆时针旋转45°,得到Rt△OA2B2,再将Rt△OA2B2绕原点O逆时针旋转45°,又得到Rt△OA3B3,……,依此规律继续旋转,得到Rt△OA2019B2019,则点B2019的坐标为 .
1.如图,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2019次得到正方形OA2019B2019C2019,那么点A2019的坐标是 .
2.如图,在平面直角坐标系中,点P1的坐标为(,),将线段OP1绕点O按顺时针方向旋转45°,再将其长度伸长为OP1的2倍,得到线段OP2;又将线段OP2绕点O按顺时针方向旋转45°,长度伸长为OP2的2倍,得到线段OP3;如此下去,得到线段OP4,OP5,…,OPn,OPn+1(n为正整数),则△OPnPn+1的面积为 .
3.如图,点D是等边△ABC内一点,将线段AD绕着点A逆时针旋转60°得到线段AE,连结CD并延长交AB于点F,连结BD,CE.
(1)求证:△ACE≌△ABD;
(2)当CF⊥AB时,∠ADB=140°,求∠ECD的度数.
4.如图,正方形ABCD中,AB=2,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF
(1)如图1,求证:AE=CF;
(2)如图2,若A,E,O三点共线,求点F到直线BC的距离.
共同特点:如果把时针、风车风轮当成一个图形,那么这些图形都可以绕着 转动一定的角度.
像这样,把一个图形绕着某一点O转动一个角度的图形变换叫做 ,点O叫做 ,转动的角叫做 ;如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个 .
旋转的三个要素: , , .
◆对应点到旋转中心的距离 .
◆对应点与旋转中心所连线段的夹角等于 .
◆旋转前、后的图形 .
图形的旋转不改变图形的形状、大小,只改变图形的位置.
中心对称图形:
绕着中心点旋转180度后能与自身重合的图形叫做中心对称图形,这个中心点叫做对称中心.
当旋转角为180°时,旋转对称图形是一个中心对称图形,所以中心对称图形是旋转对称图形的特例.
中心对称:
把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
成中心对称的性质:
1.成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
2.成中心对称的两个图形,大小相等,形状相同,两个图形全等.
3.成中心对称的两个图形,对应线段平行(或在同一直线上)且相等.
例1.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC关于原点O旋转180°得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕着点O按顺时针方向旋转90°得到△A2B2C2,画出△A2B2C2并写出各顶点的坐标.
1.如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )
A.点A与点D是对应点 B.BO=EO
C.∠ACB=∠FDE D.AB∥DE
2.下列图形中,由原图旋转得到的是( )
A. B.
C. D.
例2.如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于( )
A.55° B.60° C.65° D.80°
1.如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕点B按顺时针方向旋转一个角度到的位置,使得点A,B,在同一条直线上,则该旋转角度为( )
A.120° B.90° C.60° D.30°
2.如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
A.10 B.10 C.20 D.5
如图,△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,得到,则∠B′AC的度数是( )
A.13° B.17° C.23° D.33°
4.如图,将△ABC绕顶点C旋转得到△DEC,点A对应点D,点B对应点E,点B刚好落在DE边上,∠A=24°,∠BCD=48°,则∠ABC等于( )
A.68° B.70°
C.72° D.74°
5.台风“山竹”过去后,许多大树被大风刮倒吹折.一棵笔直的大树被风吹折后倒地,折断点为B(B点离地面为树高的处).则旋转角的度数为 .
6.将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
A. B. C. D.
例3.如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
求证:△BDE≌△BCE;
试判断四边形ABED的形状,并说明理由 .
1.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE.
(1)求证:∠A=∠EBC;
(2)若已知旋转角为40°,∠ACE=140°,求∠CED和∠BDE的度数.
例4.在线段,等腰梯形,平行四边形,矩形,正五角星,圆,正方形,等边三角形中,既是轴对称图形,又是中心对称图形的图形有( )
A.3个 B.4个 C.5个 D.6个
1.下列四个图案中,不是中心对称图形的是( )
A. B. C. D.
2.下列平面图形中,既是中心对称图形,又是轴对称图形的是( )
A.菱形 B.等边三角形 C.平行四边形 D.等腰梯形
3.(1)点P (a,b)关于原点对称的点的坐标( )
(2)点P (a,b)关于x轴对称的点的坐标( )
(3)点P (a,b)关于y轴对称的点的坐标( )
例5.如图,△BCM中,∠BMC=120°,以BC为边向三角形外作等边△ABC,把△ABM绕着点A按逆时针方向旋转60°到△CAN的位置.若BM=2,MC=3.
求:①∠AMB的度数;②求AM的长.
1.已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.
例6.如图,在正方形ABCD中,E是边AD上一点,将△ABE绕点A按逆时针方向旋转90°到△ADF的位置.已知AF=5,BE=13.
(1)求DE的长度;
(2)BE与DF是否垂直?说明你的理由.
1.如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是 .
2.如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D按逆时针方向旋转90°得到△DCM.
(1)求证:EF=MF;
(2)当AE=1时,求EF的长.
例7.如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.
(1)图中△EFD可以由 绕点 旋转 后得到;
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
1.如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想线段AE与BF的长短有何关系?说明理由;
(2)若△ABC的面积为3cm2,求四边形ABFE的面积;
(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由.
例8.如图,在平面直角坐标系中,等腰Rt△OA1B1的斜边OA1=2,且OA1在x轴的正半轴上,点B1落在第一象限内.将Rt△OA1B1绕原点O逆时针旋转45°,得到Rt△OA2B2,再将Rt△OA2B2绕原点O逆时针旋转45°,又得到Rt△OA3B3,……,依此规律继续旋转,得到Rt△OA2019B2019,则点B2019的坐标为 .
1.如图,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2019次得到正方形OA2019B2019C2019,那么点A2019的坐标是 .
2.如图,在平面直角坐标系中,点P1的坐标为(,),将线段OP1绕点O按顺时针方向旋转45°,再将其长度伸长为OP1的2倍,得到线段OP2;又将线段OP2绕点O按顺时针方向旋转45°,长度伸长为OP2的2倍,得到线段OP3;如此下去,得到线段OP4,OP5,…,OPn,OPn+1(n为正整数),则△OPnPn+1的面积为 .
3.如图,点D是等边△ABC内一点,将线段AD绕着点A逆时针旋转60°得到线段AE,连结CD并延长交AB于点F,连结BD,CE.
(1)求证:△ACE≌△ABD;
(2)当CF⊥AB时,∠ADB=140°,求∠ECD的度数.
4.如图,正方形ABCD中,AB=2,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF
(1)如图1,求证:AE=CF;
(2)如图2,若A,E,O三点共线,求点F到直线BC的距离.
同课章节目录
