数学八年级上青岛版1.3尺规作图课件7
文档属性
| 名称 | 数学八年级上青岛版1.3尺规作图课件7 |  | |
| 格式 | zip | ||
| 文件大小 | 843.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-27 08:49:28 | ||
图片预览





文档简介
课件19张PPT。1.3尺规作图
(1)求作一角等于已知角
(2)已知三边求作三角形
(3)已知两边及其夹角求作三角形复习怎样作一条线段等于已知线段 利用直尺和圆规可以作出很多几何图形,你想知道我们是如何用圆规和直尺作一条线段等于已知线段的吗?作法与示范:(1) 作射线A’C’ ;A’ C’(2) 以点A’为圆心,以AB的长为半径画弧, 交射线A’ C’于点B’, B’A’B’ 就是所求作的线段。例1:利用尺规,作一个等于 已知角.
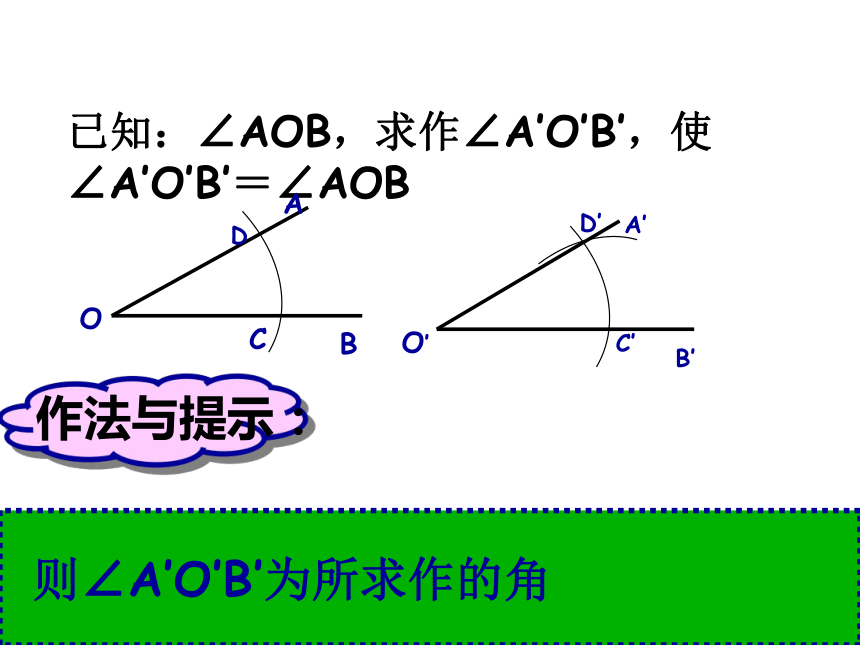
已知:∠AOB(如图).
求作:∠AˊOˊBˊ,使
∠ AˊOˊBˊ=∠AOB.
交流提纲:
⑴你是怎样思考的;
⑵讨论:按怎么样的顺序画比较方便;
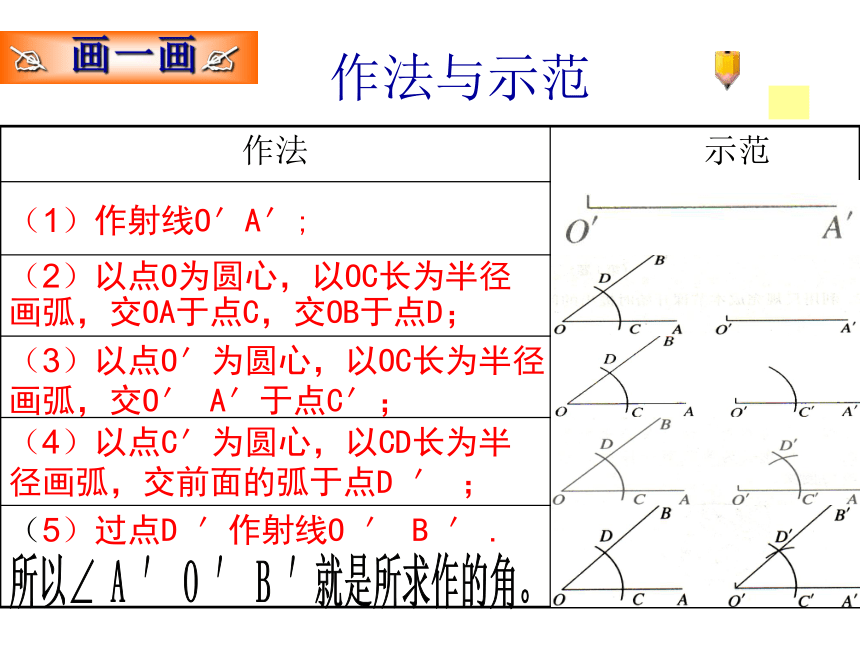
⑶画角时特别应注意什么? 思考、探究 作法与示范(1)作射线O′A′;(2)以点O为圆心,以OC长为半径画弧,交OA于点C,交OB于点D;(3)以点O′为圆心,以OC长为半径画弧,交O′ A′于点C′;(4)以点C′为圆心,以CD长为半径画弧,交前面的弧于点D ′ ;(5)过点D ′作射线O ′ B ′ .
? 画一画?所以∠ A ′ O ′ B ′就是所求作的角。已知:∠ AOB,求作:∠ AˊOˊBˊ =∠ AOB.OˊAˊCDC′D′Bˊ (1) 作射线O′A′;(2)以点O为圆心,以OC长为半径画弧,交OA于点C,交OB于点D;
(3)以点O′为圆心,以OC长为半径画弧,交O′ A′于点C′;∠ AˊOˊBˊ为所求作的角作法ABO(4)以点C′为圆心,以CD长为半径
画弧,交前面的弧于点D ′ ;(5)过点D ′作射线O ′ B ′ . 已知:∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOBCDO′B′A′D′C′这样作法正确吗?你应如何检验?连结CD,C’D’.
由作法可知O’C’=OC,O’D’=OD C’D’=CD,
所以△C’O’D’≌△COD.
则有∠C’O’D’=∠COD,即∠A’O’B’=∠AOB.
故 ∠A’O’B’即为所求作的角.做一做已知:∠α和∠β,且∠α>∠β
求作:∠α+∠β与∠α-∠β.练习:已知∠ AOB,利用尺规作
∠ A′O′B′,使∠ A′O′B′=2∠ AOB.
练习:如图,已知∠α,求作: ∠β,使∠β为 ∠α的补角。α已知三角形的三边求作三角形已知:线段a,b,c求作:△ABC,使BC=a,AC=b,AB=c(1)做线段BC=a (2)以C为圆心, b为半径画弧 (3)以B为圆心, C为半径画弧两弧相交于点A(4)连接AB,AC则△ABC为所求作的三角形已知三角形的三边求作三角形已知:线段a,b,c求作:△ABC,使BC=a,AC=b,AB=c(1)做线段BC=a, AC(2)以C为圆心, b为半径画弧 (3)以B为圆心, C为半径画弧两弧相交于点A(4)连接AB,AC则△ABC为所求作的三角形 如图,在ABC中,BC=5厘米,AC=3厘米, AB=3.5厘米, 画与△ABC全等的三角形(写出作法)分析:作三角形应先在草稿纸上画三角形的草图,
标上已知线段和角,并经过分析确定作图顺序。BMC(2)以C为圆心, 3厘米为半径画弧 (3)以B为圆心3.5厘米为半径画弧两弧相交于点A(4)连接AB,AC则△ABC为所求作的三角形(1)做线段BC=5厘米A已知三角形的两边及其夹角,求作三角形已知:线段a, c, ∠α ,求作:△ABC,使BC=a,
AB= c, ∠ABC =∠αBMDED′E′NCA (1)作∠MBN= ∠α(2)在射线B M上截取BC= a,
在射线B N上截取BA= c, (3)连接AC△ABC为所求作的三角形作法课本22页,练习:1题
2题【读一读】 :尺规作图他幼年时就表现出超人的数学天才。1795年进入格丁根大学学习。第二年他就发现正十七边形的尺规作图法。并给出可用尺规作出的正多边形的条件,解决了欧几里得以来悬而未决的问题。 通过这节课的学习活动你有哪些收获?感悟与反思
(1)求作一角等于已知角
(2)已知三边求作三角形
(3)已知两边及其夹角求作三角形复习怎样作一条线段等于已知线段 利用直尺和圆规可以作出很多几何图形,你想知道我们是如何用圆规和直尺作一条线段等于已知线段的吗?作法与示范:(1) 作射线A’C’ ;A’ C’(2) 以点A’为圆心,以AB的长为半径画弧, 交射线A’ C’于点B’, B’A’B’ 就是所求作的线段。例1:利用尺规,作一个等于 已知角.
已知:∠AOB(如图).
求作:∠AˊOˊBˊ,使
∠ AˊOˊBˊ=∠AOB.
交流提纲:
⑴你是怎样思考的;
⑵讨论:按怎么样的顺序画比较方便;
⑶画角时特别应注意什么? 思考、探究 作法与示范(1)作射线O′A′;(2)以点O为圆心,以OC长为半径画弧,交OA于点C,交OB于点D;(3)以点O′为圆心,以OC长为半径画弧,交O′ A′于点C′;(4)以点C′为圆心,以CD长为半径画弧,交前面的弧于点D ′ ;(5)过点D ′作射线O ′ B ′ .
? 画一画?所以∠ A ′ O ′ B ′就是所求作的角。已知:∠ AOB,求作:∠ AˊOˊBˊ =∠ AOB.OˊAˊCDC′D′Bˊ (1) 作射线O′A′;(2)以点O为圆心,以OC长为半径画弧,交OA于点C,交OB于点D;
(3)以点O′为圆心,以OC长为半径画弧,交O′ A′于点C′;∠ AˊOˊBˊ为所求作的角作法ABO(4)以点C′为圆心,以CD长为半径
画弧,交前面的弧于点D ′ ;(5)过点D ′作射线O ′ B ′ . 已知:∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOBCDO′B′A′D′C′这样作法正确吗?你应如何检验?连结CD,C’D’.
由作法可知O’C’=OC,O’D’=OD C’D’=CD,
所以△C’O’D’≌△COD.
则有∠C’O’D’=∠COD,即∠A’O’B’=∠AOB.
故 ∠A’O’B’即为所求作的角.做一做已知:∠α和∠β,且∠α>∠β
求作:∠α+∠β与∠α-∠β.练习:已知∠ AOB,利用尺规作
∠ A′O′B′,使∠ A′O′B′=2∠ AOB.
练习:如图,已知∠α,求作: ∠β,使∠β为 ∠α的补角。α已知三角形的三边求作三角形已知:线段a,b,c求作:△ABC,使BC=a,AC=b,AB=c(1)做线段BC=a (2)以C为圆心, b为半径画弧 (3)以B为圆心, C为半径画弧两弧相交于点A(4)连接AB,AC则△ABC为所求作的三角形已知三角形的三边求作三角形已知:线段a,b,c求作:△ABC,使BC=a,AC=b,AB=c(1)做线段BC=a, AC(2)以C为圆心, b为半径画弧 (3)以B为圆心, C为半径画弧两弧相交于点A(4)连接AB,AC则△ABC为所求作的三角形 如图,在ABC中,BC=5厘米,AC=3厘米, AB=3.5厘米, 画与△ABC全等的三角形(写出作法)分析:作三角形应先在草稿纸上画三角形的草图,
标上已知线段和角,并经过分析确定作图顺序。BMC(2)以C为圆心, 3厘米为半径画弧 (3)以B为圆心3.5厘米为半径画弧两弧相交于点A(4)连接AB,AC则△ABC为所求作的三角形(1)做线段BC=5厘米A已知三角形的两边及其夹角,求作三角形已知:线段a, c, ∠α ,求作:△ABC,使BC=a,
AB= c, ∠ABC =∠αBMDED′E′NCA (1)作∠MBN= ∠α(2)在射线B M上截取BC= a,
在射线B N上截取BA= c, (3)连接AC△ABC为所求作的三角形作法课本22页,练习:1题
2题【读一读】 :尺规作图他幼年时就表现出超人的数学天才。1795年进入格丁根大学学习。第二年他就发现正十七边形的尺规作图法。并给出可用尺规作出的正多边形的条件,解决了欧几里得以来悬而未决的问题。 通过这节课的学习活动你有哪些收获?感悟与反思
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
