数学人教A版(2019)必修第一册4.1.1n次方根与分数指数幂(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.1.1n次方根与分数指数幂(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 21:30:33 | ||
图片预览








文档简介
(共21张PPT)
第四章 指数函数与对数函数
4.1 指数
4.1.1 n次方根与分数指数幂
1.理解n次方根、根式的概念.
2.能正确运用根式的性质化简或求值,能进行根式与分数指数幂之间的相互转化.
学习目标
复习引入
幂函数
在学习幂函数时,我们把正方形场地边长c关于面积S 的函数 ,像 这样分数为指数的幂,其意义是什么呢?
如果 ,那么___叫做___的n次方根
类似地, 由于 ,______就叫做___的4次方根
由于 , _______就叫做____的5次方根
探究问题
定义:若xn=a,则x叫做a的n次方根
其中
n次方根的性质
【1】 当n是奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数.
这时,a的n次方根用符号 表示.例如
负数没有偶次方根.
【3】 0的任何次方根都是0.记作:
【2】 当n是偶数时,正数的n次方根有两个,这两个数互为相反数.正的n次方
根用 表示,负的n次方根用 表示.两者也可以合并成 .
例如
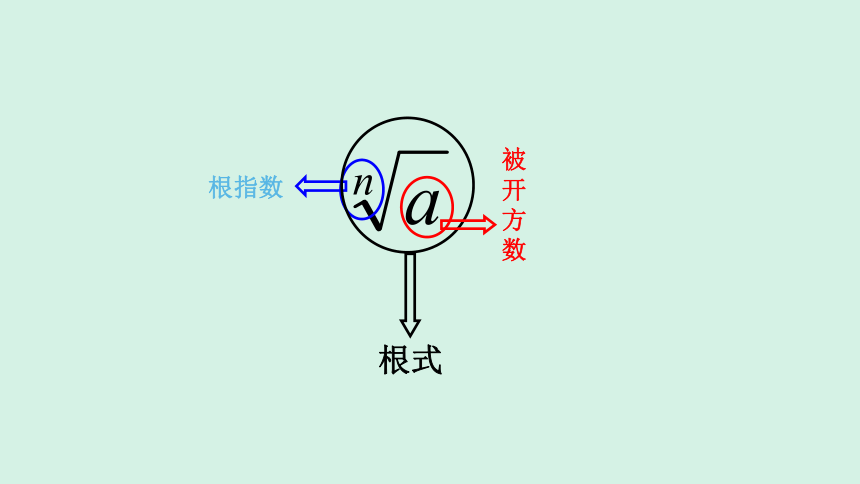
根指数
被开方数
根式
根式的性质一:
同学们,你能写出形如 的具体例子吗?
根式的性质二:
同学们,请问说明
例(1)27的立方根是 ;16的4次方根是 .
(2)已知x6=2 019,则x= .
要点笔记 根式概念问题应关注的两点(1)n的奇偶性决定了n次方根的个数;(2)n为奇数时,被开方数a的正负决定着n次方根的符号.
跟2.化简.
跟1求下列各式的值.
(1) (2)
(3) (4)
解 由题意知a-1 ≥0,即a≥1.
原式=a-1+|1-a|+1-a=a-1+a-1+1-a=a-1.
= -4
= -8
= 4
探究 根据n次方根的定义和运算,我们知道
___________________(a>0)
___________________(a>0)
也就是说,当根式的被开方数(看成幂的形式)的指数能被根指数整除时,根式可以表示成分数指数幂的形式.
思考 当根式的被开方数的指数不能被根指数整除时,根式是否也能表示为分数指数幂的形式呢?
事实上,任何一个根式都可以表示为分数指数幂的形式,例如:
, .
一般地
分数指数幂
规定正数的正分数指数幂的意义是:
所以,在条件的下,根式都可以写成分数指数幂的形式. 正数的负分数指数幂的意义与负整数指数幂的意义相仿.
规定正数的负分数指数幂的意义是:
例如,
规定0的正分数指数幂等于0,0的负分数指数幂没意义.
注意:分数指数不能随意约分. 因为约分之后可能会改变根式有意义的条件,如约分后变成了,而在实数范围内无意义.
一般的,无理数指数幂 aα(a>0,α为无理数)是一个确定的实数,幂中的指数的取值范围就从整数拓展到了有理数,并拓展到了实数. 实数指数幂是一个确定的实数.对任意实数r,s,均有下面的性质:
指数运算性质
根式化简与求值的思路及注意点:
(1)思路:首先要分清根式为奇次根式还是偶次根式,然后运用根式的性质
进行化简.
(2)注意点:
①正确区分“ ”与“ ”两式;(注意分析 是否有意义)
②运算时注意变式、整体代换,以及平方差、立方差和完全平方公式、完全立方公式的运用,必要时要进行讨论.
例1 求值:
(1)
(2)
解 (1) ;
(2)
例题精讲
例2 用分数指数幂的形式表示并计算下列各式(其中):
(1)
(2)
解 (1) ;
(2).
例题精讲
例3 计算下列各式(式中字母均是正数):
(1)
(2)
解 (1) 原式
(2) 原式
例题精讲
例4 计算下列各式(式中字母均是正数):
(3)
解 (1) 原式
例题精讲
1.次方根
2.根式
3.分数指数幂
4有理数指数幂的运算性质
课堂小结
完成习题4.1
课后作业
第四章 指数函数与对数函数
4.1 指数
4.1.1 n次方根与分数指数幂
1.理解n次方根、根式的概念.
2.能正确运用根式的性质化简或求值,能进行根式与分数指数幂之间的相互转化.
学习目标
复习引入
幂函数
在学习幂函数时,我们把正方形场地边长c关于面积S 的函数 ,像 这样分数为指数的幂,其意义是什么呢?
如果 ,那么___叫做___的n次方根
类似地, 由于 ,______就叫做___的4次方根
由于 , _______就叫做____的5次方根
探究问题
定义:若xn=a,则x叫做a的n次方根
其中
n次方根的性质
【1】 当n是奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数.
这时,a的n次方根用符号 表示.例如
负数没有偶次方根.
【3】 0的任何次方根都是0.记作:
【2】 当n是偶数时,正数的n次方根有两个,这两个数互为相反数.正的n次方
根用 表示,负的n次方根用 表示.两者也可以合并成 .
例如
根指数
被开方数
根式
根式的性质一:
同学们,你能写出形如 的具体例子吗?
根式的性质二:
同学们,请问说明
例(1)27的立方根是 ;16的4次方根是 .
(2)已知x6=2 019,则x= .
要点笔记 根式概念问题应关注的两点(1)n的奇偶性决定了n次方根的个数;(2)n为奇数时,被开方数a的正负决定着n次方根的符号.
跟2.化简.
跟1求下列各式的值.
(1) (2)
(3) (4)
解 由题意知a-1 ≥0,即a≥1.
原式=a-1+|1-a|+1-a=a-1+a-1+1-a=a-1.
= -4
= -8
= 4
探究 根据n次方根的定义和运算,我们知道
___________________(a>0)
___________________(a>0)
也就是说,当根式的被开方数(看成幂的形式)的指数能被根指数整除时,根式可以表示成分数指数幂的形式.
思考 当根式的被开方数的指数不能被根指数整除时,根式是否也能表示为分数指数幂的形式呢?
事实上,任何一个根式都可以表示为分数指数幂的形式,例如:
, .
一般地
分数指数幂
规定正数的正分数指数幂的意义是:
所以,在条件的下,根式都可以写成分数指数幂的形式. 正数的负分数指数幂的意义与负整数指数幂的意义相仿.
规定正数的负分数指数幂的意义是:
例如,
规定0的正分数指数幂等于0,0的负分数指数幂没意义.
注意:分数指数不能随意约分. 因为约分之后可能会改变根式有意义的条件,如约分后变成了,而在实数范围内无意义.
一般的,无理数指数幂 aα(a>0,α为无理数)是一个确定的实数,幂中的指数的取值范围就从整数拓展到了有理数,并拓展到了实数. 实数指数幂是一个确定的实数.对任意实数r,s,均有下面的性质:
指数运算性质
根式化简与求值的思路及注意点:
(1)思路:首先要分清根式为奇次根式还是偶次根式,然后运用根式的性质
进行化简.
(2)注意点:
①正确区分“ ”与“ ”两式;(注意分析 是否有意义)
②运算时注意变式、整体代换,以及平方差、立方差和完全平方公式、完全立方公式的运用,必要时要进行讨论.
例1 求值:
(1)
(2)
解 (1) ;
(2)
例题精讲
例2 用分数指数幂的形式表示并计算下列各式(其中):
(1)
(2)
解 (1) ;
(2).
例题精讲
例3 计算下列各式(式中字母均是正数):
(1)
(2)
解 (1) 原式
(2) 原式
例题精讲
例4 计算下列各式(式中字母均是正数):
(3)
解 (1) 原式
例题精讲
1.次方根
2.根式
3.分数指数幂
4有理数指数幂的运算性质
课堂小结
完成习题4.1
课后作业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
