数学八年级上青岛版4.3众数课件5

课件26张PPT。众数 （1）某校为学生定做校服，从全校学生中随机抽取20名同学，对1-5号校服进行试穿，这些同学选用的型号分别是1，1，1，2，2，2，2，3，3，3，3，3，3，3，3，4，4，4，5，5（2）某市2004年一月1—10日的最低气温观察上面的数据，哪种型号的选用的多？在这10个数据中，哪个数据出现的次数最多？ 在一组数据中，把出现次数最多的数据叫作这组数据的众数。 当一组数据中某数据多次重复出现时，常可以用众数作为这组数据的数值的一个代表值。试一试： 8,14,9,8,9,15,30,8这一组数据的众数是多少? 解： 8在这一组数据中出现最多（3次），因此，这组数据的众数是8。 定义: 在一组数据中，出现次数最多的数据叫做这组数据的众数．注意: (1) 众数是一组数据中出现次数最多的数据，是一组数据中的原数据，而不是相应的次数．
(2) 一组数据中的众数有时不只一个，如数据2、3、－1、2、1、3中，2和3都出现了2次，它们都是这组数据的众数．
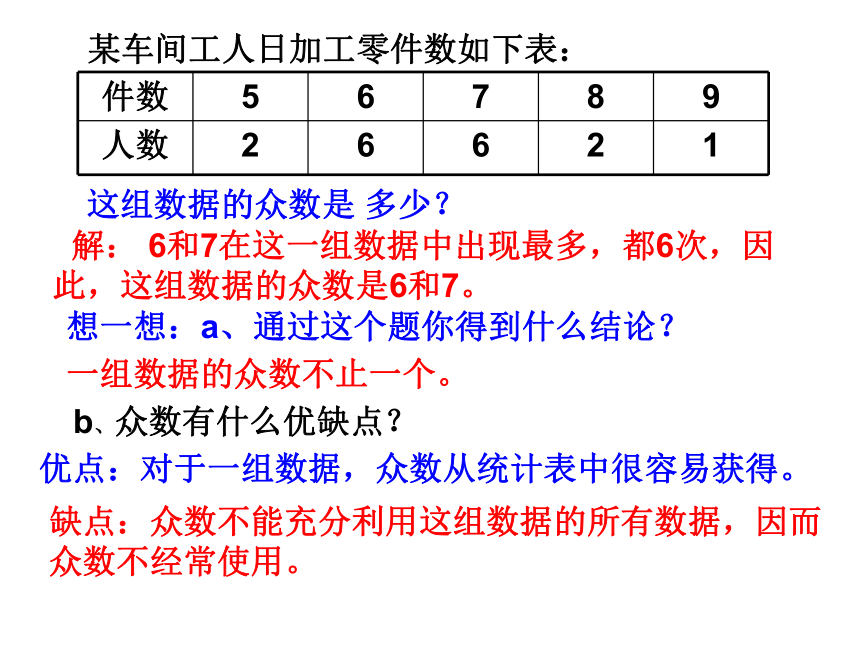
归纳 (3)如果所有数据出现的次数都一样，那么这组数据没有众数。例如：1，2，3，4，5没有众数。 某车间工人日加工零件数如下表：这组数据的众数是 多少？ 解： 6和7在这一组数据中出现最多，都6次，因此，这组数据的众数是6和7。想一想：a、通过这个题你得到什么结论？ 一组数据的众数不止一个。 b、众数有什么优缺点？ 优点：对于一组数据，众数从统计表中很容易获得。缺点：众数不能充分利用这组数据的所有数据，因而众数不经常使用。例1 某校合唱团共50名学生中，他们的年龄如下表所示，球合唱团成员年龄的众数和中位数答：众数是14岁
中位数是（13+14）/2=13.5岁例2： 下面是一家鞋店在一段时间内务种尺码男鞋的销售量统计表:思考下述问题:1、这段时间内共销售了多少双男鞋?2、销售量最多的是哪种尺码的鞋?3、这个统计表能给鞋店主什么信息?4、在这些问题中，店主最关心的问题是什么? 下面是一家鞋店在一段时间内务种尺码男鞋的销售量统计表:思考下述问题:1、这段时间内共销售了多少双男鞋?1+2+510+8+7+17+6+4=60（双）2、销售量最多的是哪种尺码的鞋?
25厘米的鞋销售最多。3、这个统计表能给鞋店主什么信息?
哪种尺码的鞋最好卖，哪种尺码的鞋不好卖。4、在这些问题中，店主最关心的问题是什么?
在这些问题中，店主最关心的问题是：哪种尺码的鞋最好卖，哪种尺码的鞋不好卖。 在这组数据中，25出现最多，也是店主最关心的数据，我们把这一数据叫做这组数据的众数。 平均数、中位数和众数都是用来代表一组数据的一些特征。
平均数反映一组数据的（ ）
中位数反映一组数据的（ ）
众数反映一组数据的 （ ）
A．平均水平 B．中等水平 C．多数水平 平均数、中位数和众数分别反映什么？ ABC思考 初二（3）班教室里，三个同学正 在为谁的数学成绩最好而争论，他们五次数学成绩分别是：探究小康： 62、 94、 95、 98、 98
小丽： 62、 62、 98、 99、 100
小芳： 40、 62、 85、 99、 99 他们都认为自己的成绩比另外两位同学好，根据你对数据的分析，应该确定哪个同学数学成绩最好呢？ 分别算出三位同学的平均数、中位数、众数： 怎样比较呢？ 小康说他的数学成绩最好，是因为他是他们三人中 最高的人。 小芳说他的数学成绩最好，是因为他是他们三人中 最高的人 小丽说他的数学成绩最好，是因为他是他们三人中 最高的人。平均数中位数众数 1、对于数据组3，3，2，3，6，3，10，3，6，3，2；
①这组数据的众数是3；
②这组数据的众数与中位数的数值不等；
③这组数据的中位数与平均数的数值相等；
④这组数据的平均数与众数的数值相等。
其中正确的结论有（ ）
（A）1个（B）2个（C）3个（D）4个A练习 2、张华是一位校鞋经销部的经理，为了解鞋子的销售情况，随机调查了9位学生的鞋子的尺码，由小到大是：20，21，21，22，22，22，22，23，23。对这组数据的分析中，张华最感兴趣的数据是（ ） (A)平均数 (B)中位数 (C)众数 C平均数、中位数和众数的异同点： （1）平均数、众数和中位数都是描述一组数据集中趋势的量；
（2）平均数、众数和中位数都有单位；
（3）平均数反映一组数据的平均水平，与这组数据中的每个数都有关系，所以应用最广，但它受极端值的影响较大；
（4）中位数只要很少计算，不受极端值影响;
（5）众数往往是我们最为关心的数据，它与各组数据出现的频数有关，不受极端值的影响. 1.一家鞋店在一段时间内销售了某种运动鞋30双，各种尺码的鞋的销售量如下：鞋的尺码/厘米
销售量
/双22122.5223523.51124724.53251假如你是老板，你最关心哪一个统计量?你会如何进货?换位思考:学以致用2.某商场服装部为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售目标,根据目标完成的情况对营业员进行适当的奖惩.为了确定一个适当的目标,商场统计了30位营业员在某月的销售额,数据如下:(单位万元)(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均的月销售额是多少?(3)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.17 18 16 13 24 15 28 26 18 19 22
17 16 19 32 30 16 14 15 26 15 32
23 17 15 15 28 28 16 19
(2)如果想让一半左右的营业员都能达到目标,你认为月销售额定为多少合适?说明理由. 某大商场策划了一次“还利给顾客”活动，凡一次购物100元以上（含100元）均可当场抽奖。奖金分配见下表：商场欺骗顾客了吗？商场提醒：平均每份奖金249元！应用 你认为商场的说法能够很好的代表中奖的一般金额吗？商场欺骗顾客了吗？说说你的看法，以后我们在遇到开奖问题应该关心什么？中奖
顾客商场在欺骗我们顾客，我们中只有两人获得80元，其他人都是20元，可气！ 商场没有欺骗顾客，因为奖金的平均数确实是249元，但是奖金的平均数不能很好地代表中奖的一般金额，91.6%的奖卷的奖金不超过80元。如果遇到开奖问题应该关心中奖金额的众数等数据信息。 鞋店老板一般最关心众数
公司老板一般以中位数为销售标准
裁判一般以平均数为选手最终得分联系实际，你会用吗？挑战自我 平均数、中位数、众数都是一组数据的代表，在什么情况下人们最关心中位数或众数？举例说明。小结：众数和平均数这三个代表数从不同的角度描述了一组数据的数值的一般水平或集中趋势，人们往往从不同的角度出发选择不同的代表数。其中平均数的应用最为广泛。试一试你的身手1.数据11, 8, 2, 7, 9, 2, 7, 3, 2, 0, 5
的众数是 ,
中位数是 .2.数据15, 20, 20, 22,30,30的众数是 ,中位数是 20和302215 3.在数据-1, 0, 4, 5, 8中插入一个数据x ,使得这组数据的中位数是3,则x= 4.数据8, 8, x, 6的众数与平均数相同,
那么它们的中位数是 5.(中考链接)5个正整数从小到大排列,
若这组数据的中位数是3,众数是7且唯
一,则这5个正整数的和是( )
A.20 B.21 C.22 D.23 28A结 束