第十二章全等三角形 单元测试(含简单答案) 2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 第十二章全等三角形 单元测试(含简单答案) 2023-2024学年人教版数学八年级上册 | 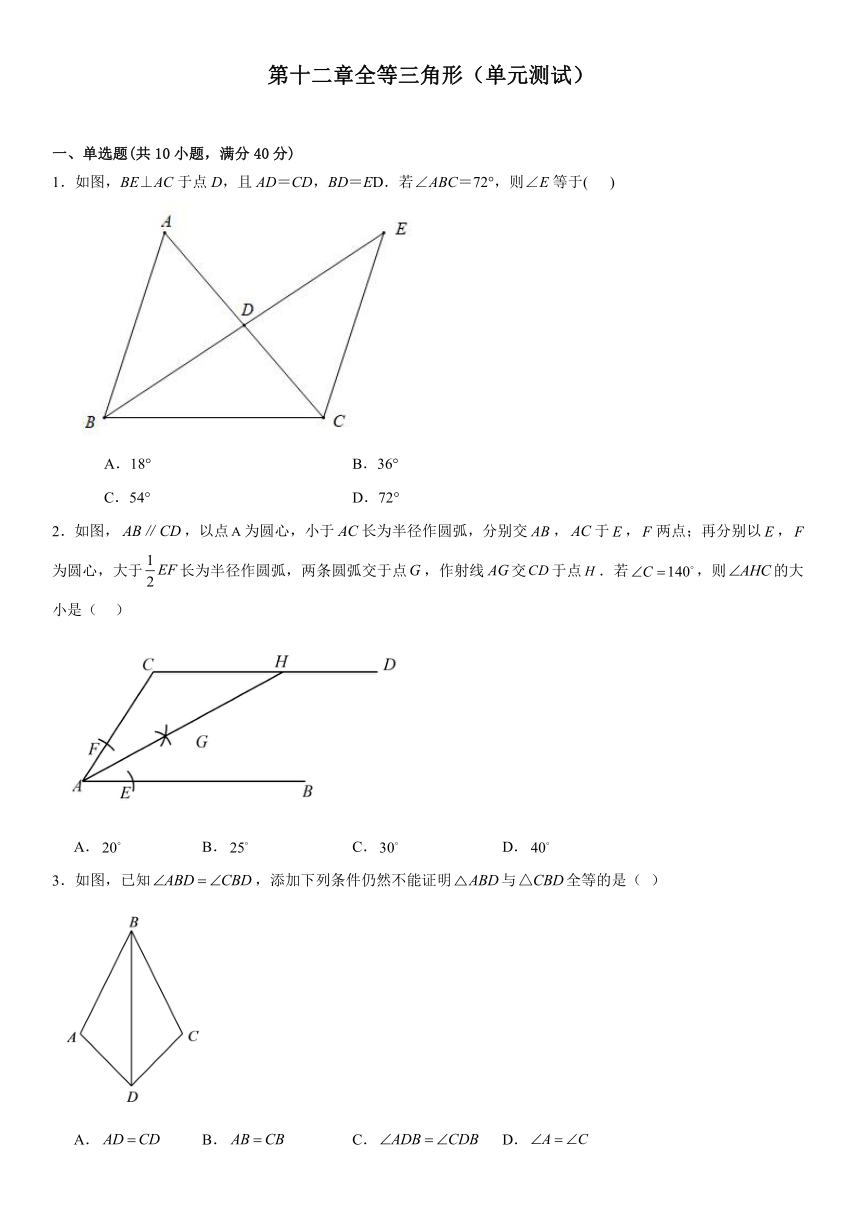 | |
| 格式 | docx | ||
| 文件大小 | 534.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 11:33:00 | ||
图片预览




文档简介
第十二章全等三角形(单元测试)
一、单选题(共10小题,满分40分)
1.如图,BE⊥AC于点D,且AD=CD,BD=ED.若∠ABC=72°,则∠E等于( )
A.18° B.36°
C.54° D.72°
2.如图,,以点为圆心,小于长为半径作圆弧,分别交,于,两点;再分别以,为圆心,大于长为半径作圆弧,两条圆弧交于点,作射线交于点.若,则的大小是( )
A. B. C. D.
3.如图,已知,添加下列条件仍然不能证明与全等的是( )
A. B. C. D.
4.如图,用尺规法作∠DEC=∠BAC,作图痕迹的正确画法是( )
A.以点E为圆心,线段AP为半径的弧
B.以点E为圆心,线段QP为半径的弧
C.以点G为圆心,线段AP为半径的弧
D.以点G为圆心,线段QP为半径的弧
5.根据下列条件能画出唯一的是( )
A. B.,,
C.,, D.,,
6.在和中,,,补充条件后仍不一定能保证,则补充的这个条件是( )
A. B. C. D.
7.如图,用直尺和圆规作∠AOB的角平分线,能得出射线OC就是∠AOB的角平分线的根据是( )
A.SSS B.SAS C.ASA D.AAS
8.如图所示中的的正方形网格中,( )
A.
B.
C.
D.
9.如图,某石油公司计划在三条公路围成的一块平地上建一个加油站,综合各种因素,要求这个加油站到三条公路的距离相等,则应建在( )
A.△ABC的三条内角平分线的交点处 B.△ABC的三条高线的交点处
C.△ABC三边的中垂线的交点处 D.△ABC的三条中线的交点处
10.如图,在中,,D,E分别为边,上的点,平分,于点F,G为的中点,延长交于点,则下列不正确的是( )
A.线段是的高 B.
C.的面积等于的面积 D.
二、填空题(共8小题,满分32分)
11.如图,,、、分别平分、、,下列结论:
①;
②;
③;
④.
其中正确的是 (填序号).
12.如图,与的顶点A、B、D在同一直线上,,,,延长分别交、于点F、G.若,,则 .
13.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是 .
14.如图,在中,.,平分交于点,则的度数是 .
15.如图,平分交于点D,于点E,若,,,则的长为 .
16.如图,中,,与的角平分线相交于点,过点作,垂足为点,则线段的长为 cm.
17.如图,D、C、F、B四点在同一条直线上,BC=DF,AC⊥BD于点C,EF⊥BD于点F,如果要添加一个条件,使△ABC≌△EDF,你添加的条件是 (注:只需写出一个条件即可).
18.如图,AD是△ABC的中线,∠ADB与∠ADC的平分线分别交AB,AC于点E,F,M是AD上的一点,且DM=DB.则给出下列结论:
①S△ABD=S△ACD;②∠EDF=90°;③MF=BE;④BE+CF>EF.
其中正确的是 (把所有正确的答案的序号都填在横线上)
三、解答题(共6小题,每题8分,满分48分)
19.为了测出池塘两端A、B的距离,小明在地面上选择了点E,D,C,使AC=CD,BC=CE,且点A,C,D和点B,C,E分别都在一条直线上,只要量出D,E的距离,就能知道A,B的距离,你认为正确吗?
解:我认为 .(填空“正确”或“不正确”)
如果认为正确,请写出证明过程;认为不正确,请举出例子.
20.如图,在中,点在边上,,的平分线交于点,过点作,垂足为,且,连接.
(1)求的度数;
(2)若,,且,直接写出的面积.
21.“魅力数学”社团活动时,张老师出示了如下问题:
如图①,已知四边形ABCD中,AC平分∠DAB,∠DAB=120°,∠B与∠D互补,试探究线段AB,AD,AC之间的数量关系;
小敏反复探索,不得其解,张老师提示道:“数学中常通过把一个问题特殊化来找到解题思路”,于是,小敏想,若将四边形ABCD特殊化,看如何解决问题:
(1)特殊情况入手
添加条件:“∠B=∠D”,如图②易知在Rt△CDA中,∠DCA=30°,所以,写出边AD与AC之间的数量关系,同理可得AB与AC的数量关系,由此得AB,AD,AC之间的数量关系;
(2)解决原来问题
受到(1)的启发,在原问题上,添加辅助线,过点C分别作AB,AD的垂线,垂足分别为E、F,如图③,请写出探究过程;
(3)解后反思
“一题多解”是数学解题的魅力之一,小敏在张老师的引导下,受探究结论的启发,结合图中的60°角,通过构造等边三角形,利用三角形全等同样解决了该问题,请在图①中作出辅助线,并简述你的探究过程.
22.△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α(0°<α≤90°),点F,G,P分别是DE,BC,CD的中点,连接PF,PG.
(1)如图①,α=90°,点D在AB上,则∠FPG= °;
(2)如图②,α=60°,点D不在AB上,判断∠FPG的度数,并证明你的结论;
(3)连接FG,若AB=5,AD=2,固定△ABC,将△ADE绕点A旋转,则PF长度的最大值为 ;PF长度的最小值为 ;
第27题
23.(1)如图1,和都是等腰三角形,即,,且,在同一条直线上.请判断线段与存在怎样的数量关系及位置关系,并说明理由.
(2)如图2,和都是等腰三角形,即,,且,请判断线段与存在怎样的数量关系及位置关系,并说明理由.
24.如图,在中,如果,分别是,的平分线且他们相交于点,设.
(1)当时,求的度数;
(2)的度数;(用含的代数式表示)
(3)当时,求证:.
参考答案:
1.B
2.A
3.A
4.D
5.D
6.C
7.A
8.B
9.A
10.A
11.①②③.
12./110度
13.3
14.
15.5
16.3
17.AB=ED或∠B=∠D或DEAB或∠A=∠E
18.①②④
19.正确
20.(1)
(2)
21.(1)AD=AC,AD+AB=AC;(2)AB+AD=AC(3)AC= AB+AD.
22.(1)∠GPF=90°;(2))∠FPG=120°;(3);
23.(1)且(2)且
24.(1)62°;(2)90°+n;
一、单选题(共10小题,满分40分)
1.如图,BE⊥AC于点D,且AD=CD,BD=ED.若∠ABC=72°,则∠E等于( )
A.18° B.36°
C.54° D.72°
2.如图,,以点为圆心,小于长为半径作圆弧,分别交,于,两点;再分别以,为圆心,大于长为半径作圆弧,两条圆弧交于点,作射线交于点.若,则的大小是( )
A. B. C. D.
3.如图,已知,添加下列条件仍然不能证明与全等的是( )
A. B. C. D.
4.如图,用尺规法作∠DEC=∠BAC,作图痕迹的正确画法是( )
A.以点E为圆心,线段AP为半径的弧
B.以点E为圆心,线段QP为半径的弧
C.以点G为圆心,线段AP为半径的弧
D.以点G为圆心,线段QP为半径的弧
5.根据下列条件能画出唯一的是( )
A. B.,,
C.,, D.,,
6.在和中,,,补充条件后仍不一定能保证,则补充的这个条件是( )
A. B. C. D.
7.如图,用直尺和圆规作∠AOB的角平分线,能得出射线OC就是∠AOB的角平分线的根据是( )
A.SSS B.SAS C.ASA D.AAS
8.如图所示中的的正方形网格中,( )
A.
B.
C.
D.
9.如图,某石油公司计划在三条公路围成的一块平地上建一个加油站,综合各种因素,要求这个加油站到三条公路的距离相等,则应建在( )
A.△ABC的三条内角平分线的交点处 B.△ABC的三条高线的交点处
C.△ABC三边的中垂线的交点处 D.△ABC的三条中线的交点处
10.如图,在中,,D,E分别为边,上的点,平分,于点F,G为的中点,延长交于点,则下列不正确的是( )
A.线段是的高 B.
C.的面积等于的面积 D.
二、填空题(共8小题,满分32分)
11.如图,,、、分别平分、、,下列结论:
①;
②;
③;
④.
其中正确的是 (填序号).
12.如图,与的顶点A、B、D在同一直线上,,,,延长分别交、于点F、G.若,,则 .
13.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是 .
14.如图,在中,.,平分交于点,则的度数是 .
15.如图,平分交于点D,于点E,若,,,则的长为 .
16.如图,中,,与的角平分线相交于点,过点作,垂足为点,则线段的长为 cm.
17.如图,D、C、F、B四点在同一条直线上,BC=DF,AC⊥BD于点C,EF⊥BD于点F,如果要添加一个条件,使△ABC≌△EDF,你添加的条件是 (注:只需写出一个条件即可).
18.如图,AD是△ABC的中线,∠ADB与∠ADC的平分线分别交AB,AC于点E,F,M是AD上的一点,且DM=DB.则给出下列结论:
①S△ABD=S△ACD;②∠EDF=90°;③MF=BE;④BE+CF>EF.
其中正确的是 (把所有正确的答案的序号都填在横线上)
三、解答题(共6小题,每题8分,满分48分)
19.为了测出池塘两端A、B的距离,小明在地面上选择了点E,D,C,使AC=CD,BC=CE,且点A,C,D和点B,C,E分别都在一条直线上,只要量出D,E的距离,就能知道A,B的距离,你认为正确吗?
解:我认为 .(填空“正确”或“不正确”)
如果认为正确,请写出证明过程;认为不正确,请举出例子.
20.如图,在中,点在边上,,的平分线交于点,过点作,垂足为,且,连接.
(1)求的度数;
(2)若,,且,直接写出的面积.
21.“魅力数学”社团活动时,张老师出示了如下问题:
如图①,已知四边形ABCD中,AC平分∠DAB,∠DAB=120°,∠B与∠D互补,试探究线段AB,AD,AC之间的数量关系;
小敏反复探索,不得其解,张老师提示道:“数学中常通过把一个问题特殊化来找到解题思路”,于是,小敏想,若将四边形ABCD特殊化,看如何解决问题:
(1)特殊情况入手
添加条件:“∠B=∠D”,如图②易知在Rt△CDA中,∠DCA=30°,所以,写出边AD与AC之间的数量关系,同理可得AB与AC的数量关系,由此得AB,AD,AC之间的数量关系;
(2)解决原来问题
受到(1)的启发,在原问题上,添加辅助线,过点C分别作AB,AD的垂线,垂足分别为E、F,如图③,请写出探究过程;
(3)解后反思
“一题多解”是数学解题的魅力之一,小敏在张老师的引导下,受探究结论的启发,结合图中的60°角,通过构造等边三角形,利用三角形全等同样解决了该问题,请在图①中作出辅助线,并简述你的探究过程.
22.△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α(0°<α≤90°),点F,G,P分别是DE,BC,CD的中点,连接PF,PG.
(1)如图①,α=90°,点D在AB上,则∠FPG= °;
(2)如图②,α=60°,点D不在AB上,判断∠FPG的度数,并证明你的结论;
(3)连接FG,若AB=5,AD=2,固定△ABC,将△ADE绕点A旋转,则PF长度的最大值为 ;PF长度的最小值为 ;
第27题
23.(1)如图1,和都是等腰三角形,即,,且,在同一条直线上.请判断线段与存在怎样的数量关系及位置关系,并说明理由.
(2)如图2,和都是等腰三角形,即,,且,请判断线段与存在怎样的数量关系及位置关系,并说明理由.
24.如图,在中,如果,分别是,的平分线且他们相交于点,设.
(1)当时,求的度数;
(2)的度数;(用含的代数式表示)
(3)当时,求证:.
参考答案:
1.B
2.A
3.A
4.D
5.D
6.C
7.A
8.B
9.A
10.A
11.①②③.
12./110度
13.3
14.
15.5
16.3
17.AB=ED或∠B=∠D或DEAB或∠A=∠E
18.①②④
19.正确
20.(1)
(2)
21.(1)AD=AC,AD+AB=AC;(2)AB+AD=AC(3)AC= AB+AD.
22.(1)∠GPF=90°;(2))∠FPG=120°;(3);
23.(1)且(2)且
24.(1)62°;(2)90°+n;
