数学八年级上青岛版5.6几何证明举例课件5
文档属性
| 名称 | 数学八年级上青岛版5.6几何证明举例课件5 |

|
|
| 格式 | zip | ||
| 文件大小 | 163.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-27 00:00:00 | ||
图片预览




文档简介
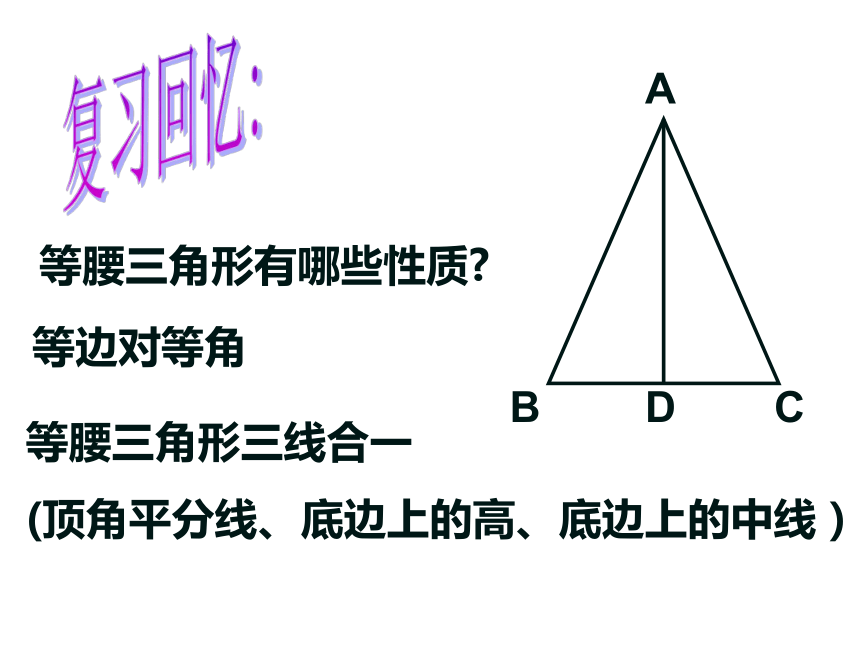
课件15张PPT。 几何证明举例等腰三角形有哪些性质?复习回忆:等边对等角等腰三角形三线合一
(顶角平分线、底边上的高、底边上的中线)E例1、如图:Rt△ABC中,∠BAC=90°,D是BC上的一点,AD=AC.
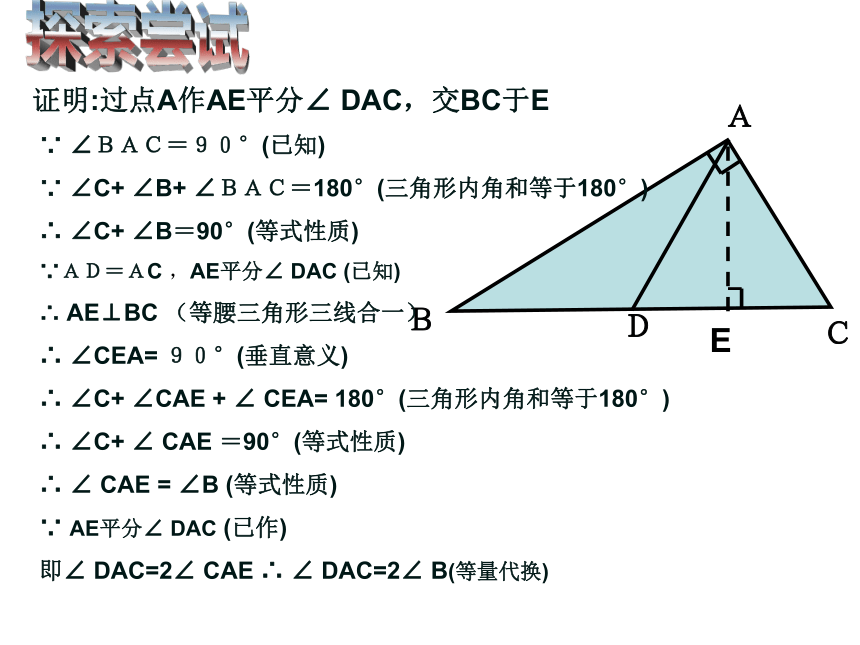
求证: ∠DAC=2∠B探索尝试E探索尝试证明:过点A作AE平分∠ DAC,交BC于E∵ ∠BAC=90°(已知)
∵ ∠C+ ∠B+ ∠BAC=180°(三角形内角和等于180°)
∴ ∠C+ ∠B=90°(等式性质)
∵AD=AC ,AE平分∠ DAC (已知)
∴ AE⊥BC (等腰三角形三线合一)
∴ ∠CEA= 90°(垂直意义)
∴ ∠C+ ∠CAE + ∠ CEA= 180°(三角形内角和等于180°)
∴ ∠C+ ∠ CAE =90°(等式性质)
∴ ∠ CAE = ∠B (等式性质)
∵ AE平分∠ DAC (已作)
即∠ DAC=2∠ CAE ∴ ∠ DAC=2∠ B(等量代换)例2、如图:在△ABC中,AB=2AC,AD平分∠BAC,AD=BD.
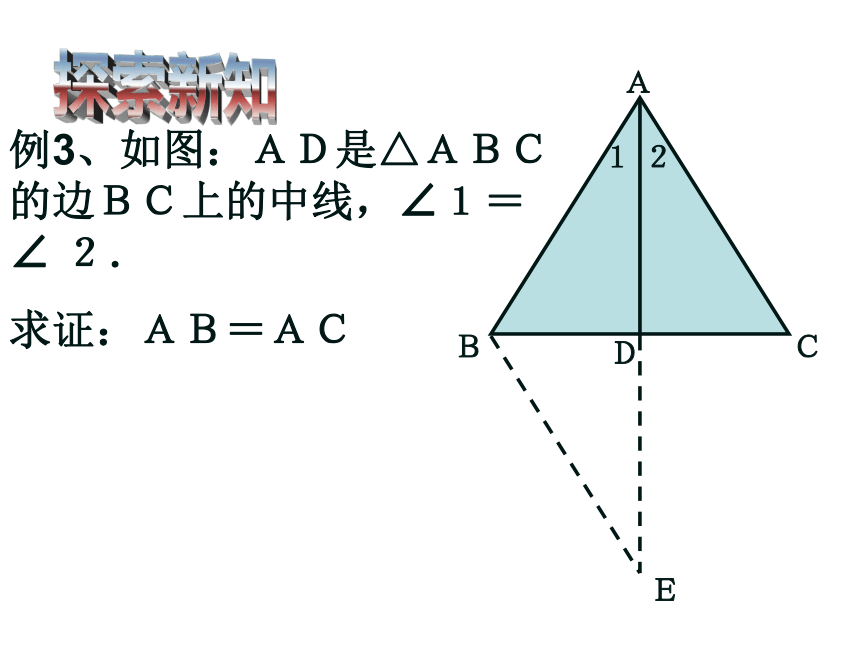
求证:AC⊥DC巩固新知EEE例3、如图:AD是△ABC的边BC上的中线,∠1= ∠ 2.
求证:AB=AC探索尝试证明△ABD≌△ACD
行吗?E例3、如图:AD是△ABC的边BC上的中线,∠1= ∠ 2.
求证:AB=AC探索新知例4、如图:AD是△ABC的边BC上的中线,BE交AC于点E,交AD于点F,AC=BF.
求证:AE=EFG分析:先证:△GBD≌△ACD
(SAS)可得:∠1= ∠ G.再证: ∠3= ∠ G可证: ∠1= ∠ 2巩固新知我来谈一谈收获和体会反思感悟1.如图,在△ABC中,
(1)如果AB=AC,可得 ,
(2)如果∠B=∠C,可得 ,∠B=∠CAB=AC2.等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
3.等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
4.等腰三角形一个角为110°,它的另外两个角为____ ___。
10 cm 或 11 cm19 cm35°,35°4.这些性质都是真命题吗?你能否用从基本事实
出发,对它们进行证明?
1.我们学习了证明的相关知识,你还记得我们依据
哪些基本事实,证明了哪些定理?你能说出来吗?
2.我们已经学习过等腰三角形,我们来回忆一下
下列几个问题:
(1)什么叫做等腰三角形?(等腰三角形的定义)
(2)等腰三角形有哪些性质?等腰三角形的两底角相等(简称等边对等角)。等腰三角形的顶角平分线、底边上的中线、底边上的高
互相重合(等腰三角形的三线合一)。
3.上述性质你是怎么得到的?轴对称的性质
1、等腰三角形常添的辅助线是底边上的高2、利用延长中线的一倍构造中心对称的两个全等三角形2、倍长中线法练习1、如图:在Rt△ABC中,∠C=90°, CD是AB边上的中线.
求证:CD= ABED应用内化练习2 、如图:在△ABC中,AB=AC, CD⊥AB.
求证: ∠ A=2∠1E应用内化作业:练习册17.2(6)谢谢
(顶角平分线、底边上的高、底边上的中线)E例1、如图:Rt△ABC中,∠BAC=90°,D是BC上的一点,AD=AC.
求证: ∠DAC=2∠B探索尝试E探索尝试证明:过点A作AE平分∠ DAC,交BC于E∵ ∠BAC=90°(已知)
∵ ∠C+ ∠B+ ∠BAC=180°(三角形内角和等于180°)
∴ ∠C+ ∠B=90°(等式性质)
∵AD=AC ,AE平分∠ DAC (已知)
∴ AE⊥BC (等腰三角形三线合一)
∴ ∠CEA= 90°(垂直意义)
∴ ∠C+ ∠CAE + ∠ CEA= 180°(三角形内角和等于180°)
∴ ∠C+ ∠ CAE =90°(等式性质)
∴ ∠ CAE = ∠B (等式性质)
∵ AE平分∠ DAC (已作)
即∠ DAC=2∠ CAE ∴ ∠ DAC=2∠ B(等量代换)例2、如图:在△ABC中,AB=2AC,AD平分∠BAC,AD=BD.
求证:AC⊥DC巩固新知EEE例3、如图:AD是△ABC的边BC上的中线,∠1= ∠ 2.
求证:AB=AC探索尝试证明△ABD≌△ACD
行吗?E例3、如图:AD是△ABC的边BC上的中线,∠1= ∠ 2.
求证:AB=AC探索新知例4、如图:AD是△ABC的边BC上的中线,BE交AC于点E,交AD于点F,AC=BF.
求证:AE=EFG分析:先证:△GBD≌△ACD
(SAS)可得:∠1= ∠ G.再证: ∠3= ∠ G可证: ∠1= ∠ 2巩固新知我来谈一谈收获和体会反思感悟1.如图,在△ABC中,
(1)如果AB=AC,可得 ,
(2)如果∠B=∠C,可得 ,∠B=∠CAB=AC2.等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
3.等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
4.等腰三角形一个角为110°,它的另外两个角为____ ___。
10 cm 或 11 cm19 cm35°,35°4.这些性质都是真命题吗?你能否用从基本事实
出发,对它们进行证明?
1.我们学习了证明的相关知识,你还记得我们依据
哪些基本事实,证明了哪些定理?你能说出来吗?
2.我们已经学习过等腰三角形,我们来回忆一下
下列几个问题:
(1)什么叫做等腰三角形?(等腰三角形的定义)
(2)等腰三角形有哪些性质?等腰三角形的两底角相等(简称等边对等角)。等腰三角形的顶角平分线、底边上的中线、底边上的高
互相重合(等腰三角形的三线合一)。
3.上述性质你是怎么得到的?轴对称的性质
1、等腰三角形常添的辅助线是底边上的高2、利用延长中线的一倍构造中心对称的两个全等三角形2、倍长中线法练习1、如图:在Rt△ABC中,∠C=90°, CD是AB边上的中线.
求证:CD= ABED应用内化练习2 、如图:在△ABC中,AB=AC, CD⊥AB.
求证: ∠ A=2∠1E应用内化作业:练习册17.2(6)谢谢
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
