数学八年级下青岛版7.8实数课件6

课件32张PPT。实数
1、掌握实数的概念及分类。（重点）
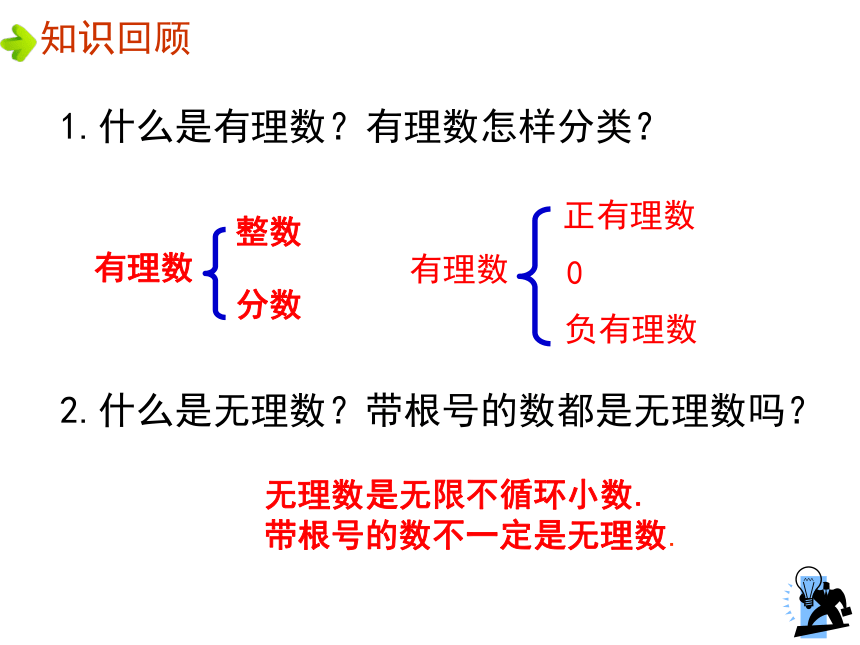
2、掌握实数与数轴的关系。（难点）学习目标知识回顾1.什么是有理数？有理数怎样分类？ 整数分数有理数正有理数负有理数有理数02.什么是无理数？带根号的数都是无理数吗？ 无理数是无限不循环小数.
带根号的数不一定是无理数.（相邻两个3之间的7的个数逐次加1） 有理数集合 无理数集合把下列各数分别填入相应的集合内.试一试自主学习自学课本p153、p154部分（5分钟）完成下列题目：
1、知道什么是实数。
2、将153页实数的分类完成。
3、实数与数轴上的点是一一对应的，你能解释“一一对应”的意思吗？
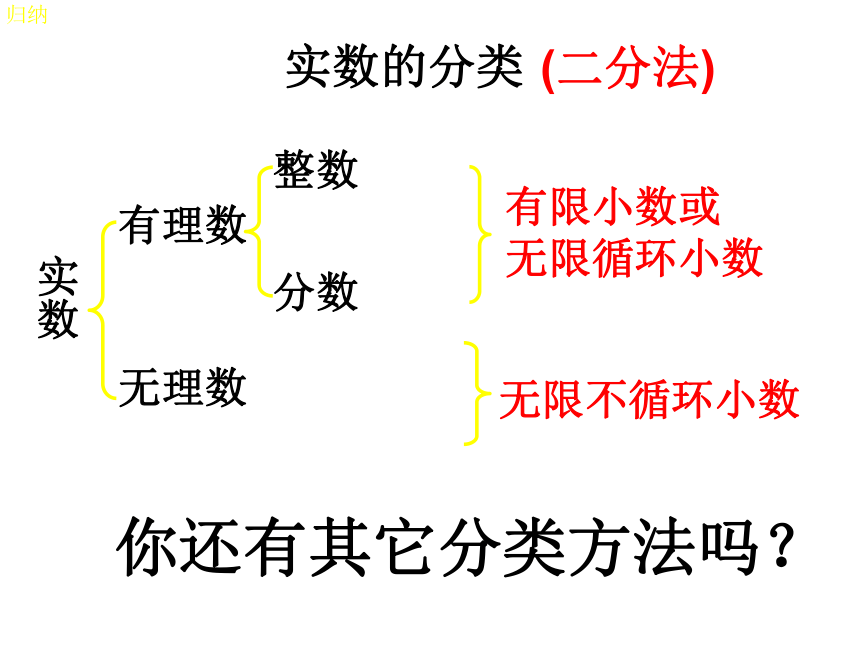
归纳实数的分类实数有理数无理数整数分数有限小数或
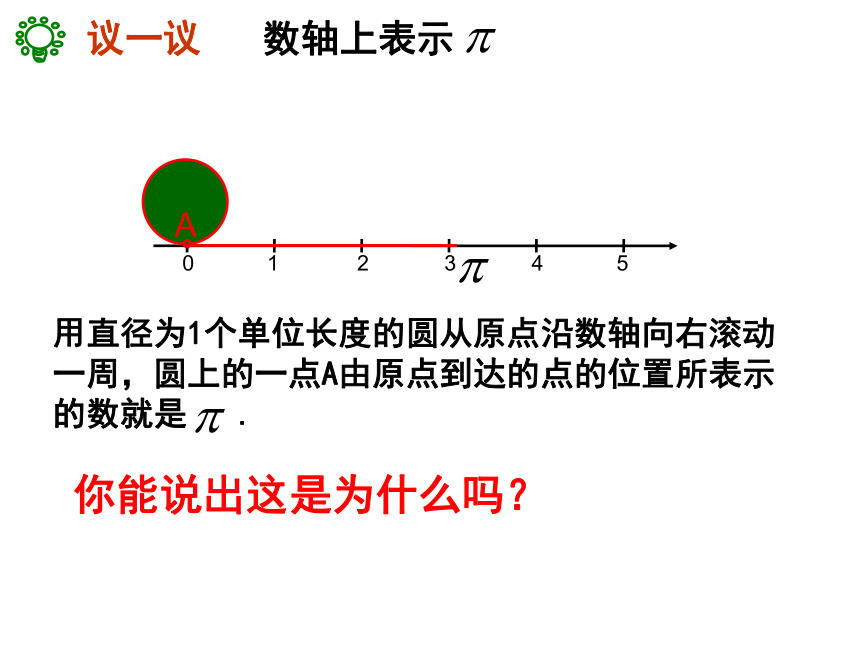
无限循环小数无限不循环小数你还有其它分类方法吗？(二分法)归纳实数的分类实数正实数负实数正有理数正无理数你知道怎样区分有理数和无理数吗？0负无理数负有理数(三分法)一、判断：1.实数不是有理数就是无理数。（ ）2.无理数都是无限不循环小数。（ ）3.无理数都是无限小数。（ ）4.带根号的数都是无理数。（ ）5.无理数一定都带根号。（ ）6.两个无理数之积不一定是无理数。（ ）7.两个无理数之和一定是无理数。（ ）8.数轴上的任何一点都可以表示实数。（ ）×××二、把下列各数填入相应的集合内：有理数集合：无理数集合：整数集合：分数集合：实数集合：议一议数轴上表示用直径为1个单位长度的圆从原点沿数轴向右滚动
一周，圆上的一点A由原点到达的点的位置所表示
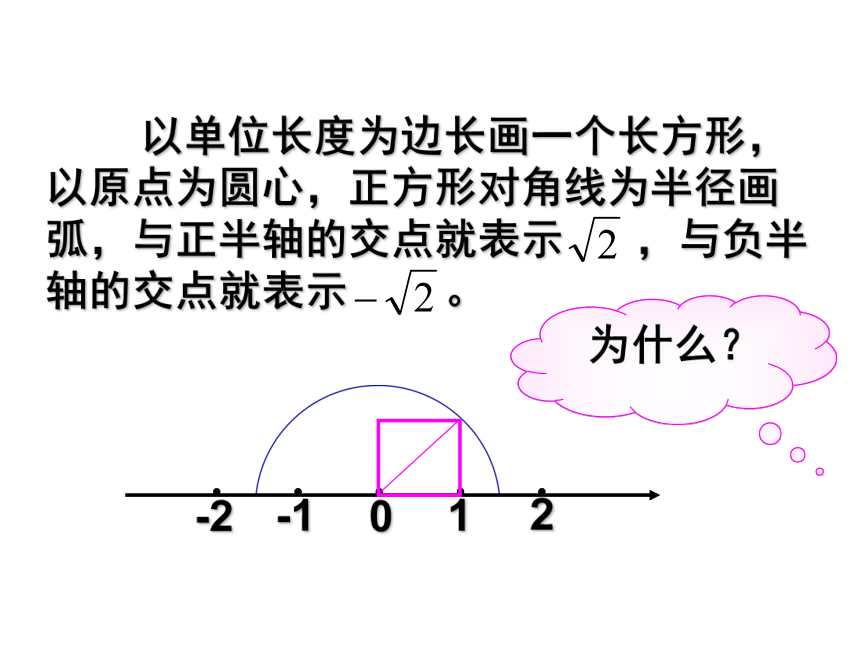
的数就是 .a你能说出这是为什么吗？ 以单位长度为边长画一个长方形，以原点为圆心，正方形对角线为半径画弧，与正半轴的交点就表示 ，与负半轴的交点就表示 。 为什么？归纳 1、每一个有理数都可以用数轴上的点
表示；2、每一个无理数都可以用数轴上的点
表示；实数与数轴上的点是一一对应的同样的,平面直角坐标系中的点与有序实数对是一一对应的. 当数从有理数扩充到实数以后，有理数关于相反数和绝对值的意义同样适合于实数。-π的相反数是 　 ；0的相反数是 　 ；的相反数是 ；ππ00数a的相反数是-a，这里a表示任意一个实数。 一个正实数的绝对值是它本身；一个负实数的绝对值是它的相反数；0的绝对值是0。思考填空２、 的相反数是 ，绝对值是 ．３、绝对值等于 的数是 ， 的平 方 是 ．１、正实数的绝对值是 ，０的绝对值是 ，负实数的绝对值是　 .它本身0它的相反数5、一个数的绝对值是 ，则这个数是 .练习2、填空：
（1） 的相反数是__________ （5） 绝对值是 _________ （2） 的倒数是____,（3）｜ ｜=___________（4）绝对值等于 的数是 _________ 的平方 是___ 　．例题例1 （1） 求的绝对值；解： （2）已知一个数的绝对值是 ，求这个值。解：∴绝对值为 的数是 或 。 先算_________,然后算______,最后算_____;有括号,先算 .
如果是同级运算,应按从________的顺序进行.
乘方、开方乘除加减括号里边的左到右实数的运算顺序实数的运算 当数从有理数扩充到实数以后，实 数之间不仅可以进行加、减、乘、除（除数不为0）、乘方运算，而且正数及0可以进行开平方运算，任意一个实数可以进行立方运算。在进行实数的运算时，有理数的运算法则及运算性质等同样适用。例题例2 计算下列各式的值：解：===== 在实数运算中，当遇到无理数并且需要求出结果的近似值时，可以按照所要求的精确度用相应的近似有限小数去代替无理数，再进行计算。什么是有效数字？ 从左边第一个不是零的数开始数起，到最后一个数字就叫有效数字 。例题例3 计算：解：练习∵ ≥0，（b-1）2≥0，｜c +3｜≥0解：∴a=-2, b=1, c=-3则a+b+c=-2+1-3= - 4 如图，数轴上表示1、 的对应点分别是A、B，点B关于点A的对称点为C，则C点所表示的数是( )1-C思考2、8的立方根与4的算术平方根的和是( )
A 0 B 4
C -4 D 0或-43、已知：a、b互为相反数，c、d为倒数，x的绝对值等于1，求a+b+x2-cdx的值。巩固练习每一个实数都可以用数轴上的一个点来表示；
反之，数轴上的每一个点都代表一个实数。同样的,平面直角坐标系中的点与有序实数对是一一对应的.精讲点拨实数与数轴上的点
是 的关系。一一对应小结与思考1、实数的分类。
2、实数与数轴上的点的对应关系。
3、实数的运算：有理数的相反数，绝对值等概念，大小比较，运算法则，运算律对实数仍适用。拓展延伸1、下列各数， ， ，0 ， ，2- ， ， ，0.020020002 …（每两个2之间多一个0）中无理数有（ ）
A、6个 B、5个 C、4个 D、3个C 4、　　　　的绝对值是 。４2、- 绝对值是 ,相反数是 ,倒数是 . 作业1、课本P156习题A组。
2、习题B组（选做）。谢谢大家