5.1.1变化率问题(第1课时) 课件(共22张PPT)
文档属性
| 名称 | 5.1.1变化率问题(第1课时) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 14.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 21:56:45 | ||
图片预览







文档简介
(共22张PPT)
人教A版(2019)高中数学选择性必修二
5.1.1变化率问题
第一课时
17世纪中叶,牛顿和莱布尼茨各自独立地创立了微积分
牛顿偏重从物理问题出发,应用了运动学的原理,如瞬时速度中的“微分”、运动变量的“积分”等概念.
莱布尼茨从几何学问题出发,用分析法引进微积分,得出运算法则,比牛顿的更为规范和严密.
章前导入
微积分的创立与处理四类科学问题直接相关
1
求物体在任意时刻的速度与加速度
2
求曲线的切线
3
求函数的最大值与最小值
4
求长度、面积、体积和重心等
导数是微积分的核心概念之一,是现代数学的基本概念,蕴含着微积分的基本思想;导数定量地刻画了函数的局部变化,是研究函数增减、变化快慢、最大(小)值等性质的基本方法.
导数的本质是什么?
课程标准
1.通过实例分析,经历由平均变化率过渡到瞬间变化率的过程,了解导数概念的实际背景,知道导数是关于瞬间变化率的数学表达,体会导数的内涵与思想;
2.体会极限思想;
3.通过函数图象直接理解导数的几何意义。
一
二
三
学习目标
会求函数在某一点附近的平均变化率,理解函数的平均变化率,瞬时变化率及瞬时速度的概念
会求抛物线的切线斜率,体会数学的极限思想
通过本节课的学习,培养起数学抽象、逻辑推理及数学运算的核心素养.
学习目标
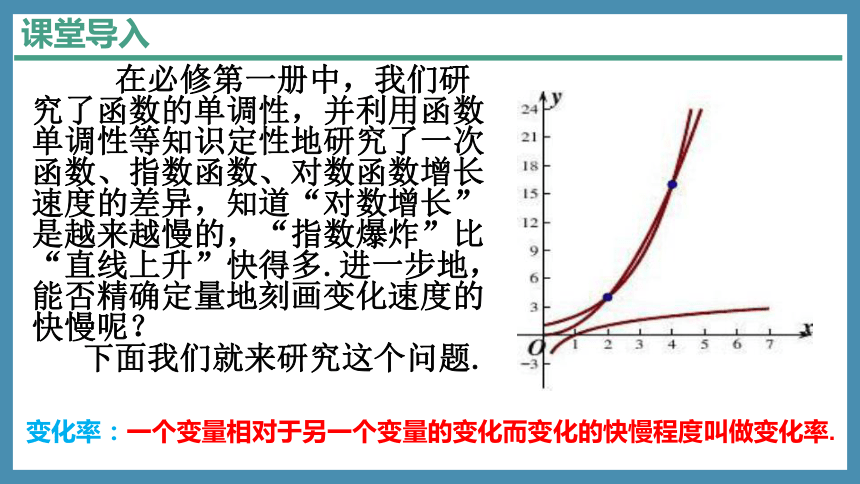
课堂导入
在必修第一册中,我们研究了函数的单调性,并利用函数单调性等知识定性地研究了一次函数、指数函数、对数函数增长速度的差异,知道“对数增长”是越来越慢的,“指数爆炸”比“直线上升”快得多.进一步地,能否精确定量地刻画变化速度的快慢呢?
下面我们就来研究这个问题.
变化率:一个变量相对于另一个变量的变化而变化的快慢程度叫做变化率.
创设情境
问题1 高台跳水运动员的速度
新知探究:变化率问题
新知探究:变化率问题
问题1 高台跳水运动员的速度
在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系:
如何描述运动员从起跳到入水的过程中运动的快慢程度呢?
视频中,运动员从起跳到入水的过程中,在上升阶段运动得越来越慢,在下降阶段运动得越来越快。我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度近似地描述他的运动状态.
请计算对应时间段的平均速度:
新知探究:变化率问题
新知探究:变化率问题
要精确地描述非匀速直线运动,就要知道物体在每一时刻运动的快慢程度.
再计算:
追问1:(1)运动员在这段时间里是静止的吗
(2)平均速度能准确反映运动员的运动状态吗
(1)在这段时间内,运动员并不处于静止状态.
(2)用平均速度不能准确反映运动员在这段时间内里的运动状态.
新知探究:变化率问题
为了精确刻画运动员的运动状态,需要引入瞬时速度的概念. 我们把物体在某一时刻的速度称为瞬时速度(instantaneous velocity).
追问2 瞬时速度与平均速度有什么关系
你能利用这种关系求运动员在t=1s时的瞬时速度吗
设运动员在时刻附近某一时间段内的平均速度是
可以想象,如果不断缩短这一时间段的长度,那么将越来越趋近于运动员在时刻的瞬时速度.
新知探究:变化率问题
问题 运动员在t=1s时的瞬时速度是多少?
Δt是时间改变量,可以是正值,也可以是负值,但不为0.
为了提高近似表示的精确度,我们不断缩短时间间隔,得到如下表格.
Δt < 0 Δt > 0
-0.01 0.01
-0.001 0.001
-0.0001 0.0001
-0.00001 0.00001
-0.000001 0.000001
-4.951
-4.9951
-4.99951
-4.999951
-4.9999951
-5.049
-5.0049
-5.00049
-5.000049
-5.0000049
通过观察可得,当 t无限趋近于0,即无论t从小于1的一边,还是从大于1的一边无限趋近于1时,平均速度都无限趋近于-5.
归纳总结
(1)求物体运动路程与时间的关系s=s(t);
(2)求时间改变量Δt,位移改变量Δs=s(t0+Δt)-s(t0);
求瞬时速度的步骤
方法归纳
新知应用
思考 (1) 求运动员在t=2 s时的瞬时速度;
(2) 如何求运动员从起跳到入水过程中在某一时刻t0的瞬时速度
新知应用
思考 (1) 求运动员在t=2 s时的瞬时速度;
(2) 如何求运动员从起跳到入水过程中在某一时刻t0的瞬时速度
解:
因此运动员在某一时刻 t0 的瞬时速度为
平均速度与瞬时速度的关系:
1. 平均速度:
运动员在时间段[t0, t0+Δt]内的平均速度为
当Δt无限趋近于0时,平均速度的极限为瞬时速度,记为
2. 瞬时速度:
两者都刻画物体的运动状态,瞬时速度是平均速度的极限值.
归纳总结
1.本节课收获了哪些知识?
平均速度
瞬时速度
瞬时速度的本质是平均速度的极限.
(1) 平均速度:
(2) 瞬时速度:
2.求物体在时刻t0的瞬时速度一般步骤:
课堂小结
巩固练习
1. 求问题1中高台跳水运动员在t=0.5 s时的瞬时速度.
课本P61
巩固练习
课本P61
2. 火箭发射t s后,其高度(单位: m)为h(t)=0.9t2. 求:
(1) 在1≤t≤2这段时间里,火箭爬高的平均速度;
(2) 发射后第10 s时,火箭爬高的瞬时速度.
巩固练习
课本P62
3. 一个小球从5 m的高处自由下落,其位移y (单位: m)与时间t (单位: s) 之间的关系为 y(t)=-4.9t2 . 求t =1 s时小球的瞬时速度.
人教A版(2019)高中数学选择性必修二
5.1.1变化率问题
第一课时
17世纪中叶,牛顿和莱布尼茨各自独立地创立了微积分
牛顿偏重从物理问题出发,应用了运动学的原理,如瞬时速度中的“微分”、运动变量的“积分”等概念.
莱布尼茨从几何学问题出发,用分析法引进微积分,得出运算法则,比牛顿的更为规范和严密.
章前导入
微积分的创立与处理四类科学问题直接相关
1
求物体在任意时刻的速度与加速度
2
求曲线的切线
3
求函数的最大值与最小值
4
求长度、面积、体积和重心等
导数是微积分的核心概念之一,是现代数学的基本概念,蕴含着微积分的基本思想;导数定量地刻画了函数的局部变化,是研究函数增减、变化快慢、最大(小)值等性质的基本方法.
导数的本质是什么?
课程标准
1.通过实例分析,经历由平均变化率过渡到瞬间变化率的过程,了解导数概念的实际背景,知道导数是关于瞬间变化率的数学表达,体会导数的内涵与思想;
2.体会极限思想;
3.通过函数图象直接理解导数的几何意义。
一
二
三
学习目标
会求函数在某一点附近的平均变化率,理解函数的平均变化率,瞬时变化率及瞬时速度的概念
会求抛物线的切线斜率,体会数学的极限思想
通过本节课的学习,培养起数学抽象、逻辑推理及数学运算的核心素养.
学习目标
课堂导入
在必修第一册中,我们研究了函数的单调性,并利用函数单调性等知识定性地研究了一次函数、指数函数、对数函数增长速度的差异,知道“对数增长”是越来越慢的,“指数爆炸”比“直线上升”快得多.进一步地,能否精确定量地刻画变化速度的快慢呢?
下面我们就来研究这个问题.
变化率:一个变量相对于另一个变量的变化而变化的快慢程度叫做变化率.
创设情境
问题1 高台跳水运动员的速度
新知探究:变化率问题
新知探究:变化率问题
问题1 高台跳水运动员的速度
在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系:
如何描述运动员从起跳到入水的过程中运动的快慢程度呢?
视频中,运动员从起跳到入水的过程中,在上升阶段运动得越来越慢,在下降阶段运动得越来越快。我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度近似地描述他的运动状态.
请计算对应时间段的平均速度:
新知探究:变化率问题
新知探究:变化率问题
要精确地描述非匀速直线运动,就要知道物体在每一时刻运动的快慢程度.
再计算:
追问1:(1)运动员在这段时间里是静止的吗
(2)平均速度能准确反映运动员的运动状态吗
(1)在这段时间内,运动员并不处于静止状态.
(2)用平均速度不能准确反映运动员在这段时间内里的运动状态.
新知探究:变化率问题
为了精确刻画运动员的运动状态,需要引入瞬时速度的概念. 我们把物体在某一时刻的速度称为瞬时速度(instantaneous velocity).
追问2 瞬时速度与平均速度有什么关系
你能利用这种关系求运动员在t=1s时的瞬时速度吗
设运动员在时刻附近某一时间段内的平均速度是
可以想象,如果不断缩短这一时间段的长度,那么将越来越趋近于运动员在时刻的瞬时速度.
新知探究:变化率问题
问题 运动员在t=1s时的瞬时速度是多少?
Δt是时间改变量,可以是正值,也可以是负值,但不为0.
为了提高近似表示的精确度,我们不断缩短时间间隔,得到如下表格.
Δt < 0 Δt > 0
-0.01 0.01
-0.001 0.001
-0.0001 0.0001
-0.00001 0.00001
-0.000001 0.000001
-4.951
-4.9951
-4.99951
-4.999951
-4.9999951
-5.049
-5.0049
-5.00049
-5.000049
-5.0000049
通过观察可得,当 t无限趋近于0,即无论t从小于1的一边,还是从大于1的一边无限趋近于1时,平均速度都无限趋近于-5.
归纳总结
(1)求物体运动路程与时间的关系s=s(t);
(2)求时间改变量Δt,位移改变量Δs=s(t0+Δt)-s(t0);
求瞬时速度的步骤
方法归纳
新知应用
思考 (1) 求运动员在t=2 s时的瞬时速度;
(2) 如何求运动员从起跳到入水过程中在某一时刻t0的瞬时速度
新知应用
思考 (1) 求运动员在t=2 s时的瞬时速度;
(2) 如何求运动员从起跳到入水过程中在某一时刻t0的瞬时速度
解:
因此运动员在某一时刻 t0 的瞬时速度为
平均速度与瞬时速度的关系:
1. 平均速度:
运动员在时间段[t0, t0+Δt]内的平均速度为
当Δt无限趋近于0时,平均速度的极限为瞬时速度,记为
2. 瞬时速度:
两者都刻画物体的运动状态,瞬时速度是平均速度的极限值.
归纳总结
1.本节课收获了哪些知识?
平均速度
瞬时速度
瞬时速度的本质是平均速度的极限.
(1) 平均速度:
(2) 瞬时速度:
2.求物体在时刻t0的瞬时速度一般步骤:
课堂小结
巩固练习
1. 求问题1中高台跳水运动员在t=0.5 s时的瞬时速度.
课本P61
巩固练习
课本P61
2. 火箭发射t s后,其高度(单位: m)为h(t)=0.9t2. 求:
(1) 在1≤t≤2这段时间里,火箭爬高的平均速度;
(2) 发射后第10 s时,火箭爬高的瞬时速度.
巩固练习
课本P62
3. 一个小球从5 m的高处自由下落,其位移y (单位: m)与时间t (单位: s) 之间的关系为 y(t)=-4.9t2 . 求t =1 s时小球的瞬时速度.
