专题17.3勾股定理 巩固篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题17.3勾股定理 巩固篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 22:33:11 | ||
图片预览


文档简介
专题17.3 勾股定理(巩固篇)(专项练习)
一、单选题
1.下列各组数中,是勾股数的是( )
A.3,4,7 B.7,24,25 C.,, D.3,-4,5
2.平面直角坐标系内,点到原点的距离是( )
A.2 B.3 C. D.2或3
3.如图,在直角三角形中,,,,则( )
A.6 B. C.4 D.
4.如图,正方形网格中,每一小格的边长为1.网格内有,则的度数是( )
A. B. C. D.
5.如图,在△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A.29 B.32 C.36 D.45
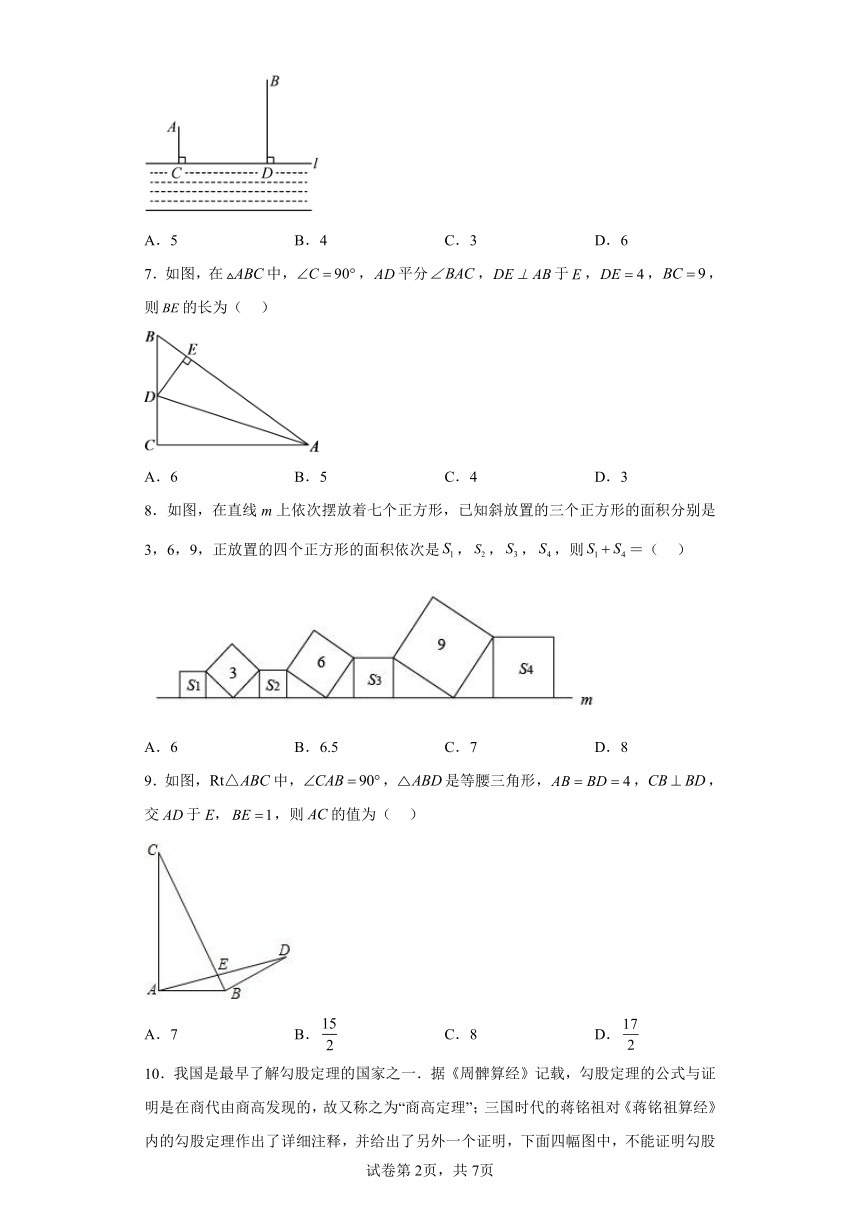
6.如图,要在河边l上修建一个水泵站,分别向A村和B村送水,已知A村、B村到河边的距离分别1km和3km,且相距3km,则铺水管的最短长度是( )km
A.5 B.4 C.3 D.6
7.如图,在中,,平分,于,,,则的长为( )
A.6 B.5 C.4 D.3
8.如图,在直线m上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是3,6,9,正放置的四个正方形的面积依次是,,,,则=( )
A.6 B.6.5 C.7 D.8
9.如图,中,,是等腰三角形,,,交于E,,则的值为( )
A.7 B. C.8 D.
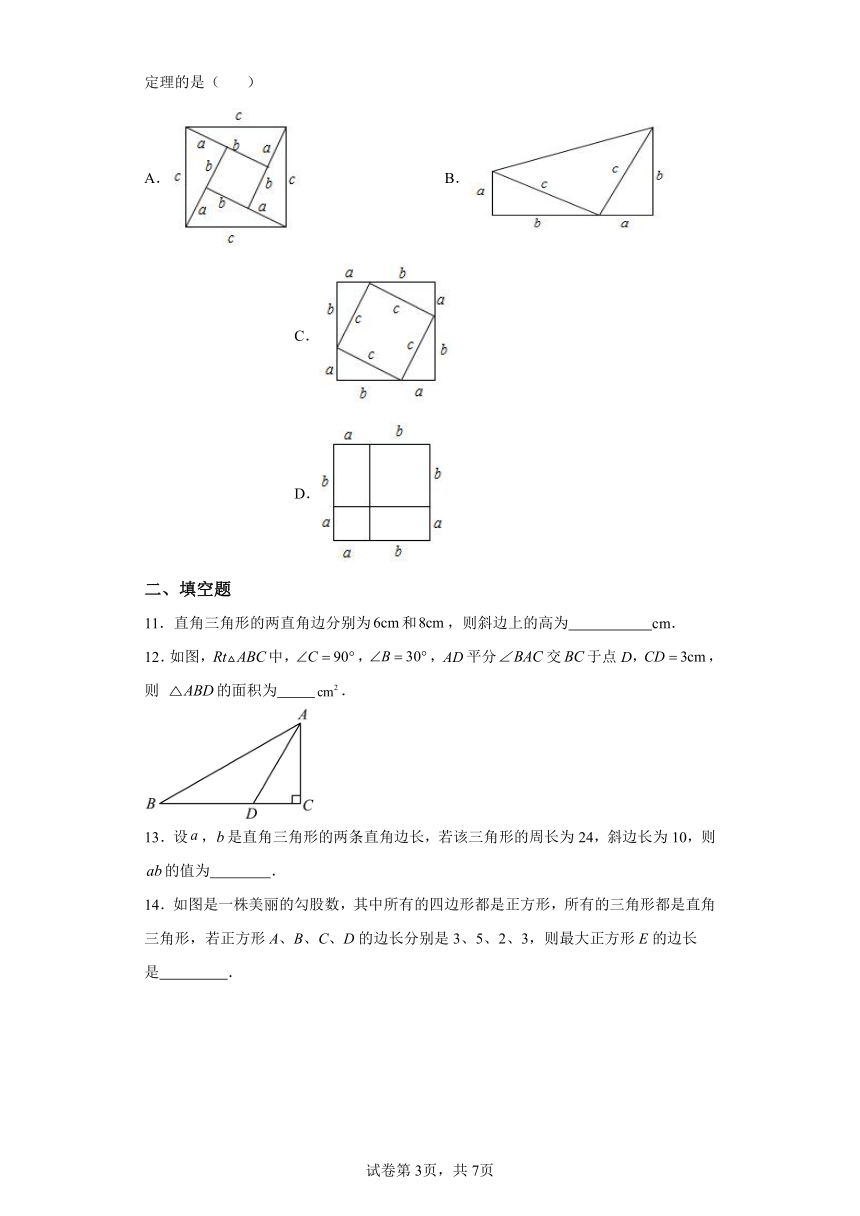
10.我国是最早了解勾股定理的国家之一.据《周髀算经》记载,勾股定理的公式与证明是在商代由商高发现的,故又称之为“商高定理”;三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释,并给出了另外一个证明,下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
二、填空题
11.直角三角形的两直角边分别为和,则斜边上的高为 cm.
12.如图,中,,,平分交于点D,,则 的面积为 .
13.设,是直角三角形的两条直角边长,若该三角形的周长为24,斜边长为10,则的值为 .
14.如图是一株美丽的勾股数,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的边长是 .
15.如图所示,点A、B分别是坐标轴上的点,且,轴,点D在x轴负半轴上,,连接OC、BD相交于点E,若四边形ACED的面积为,OE长为1,则点A的坐标为 .
16.在一个长为,宽为3的长方形草地上,如图摆放着一根三棱柱的木块,它的侧棱EF平行于AD,且棱长大于场地宽AD,木块的主视图为等腰直角三角形,且底边上的高为1,一只蚂蚁从点A处到C处需要走的最短路程是 .
17.如图所示,图甲是第七届国际数学教育大会(ICME)的会徽,主体图案是由如图乙的一连串直角三角形演化而成,其中,现把图乙中的直角三角形继续作下去,则 , ;若的值是整数,且,则符合条件的有 个.
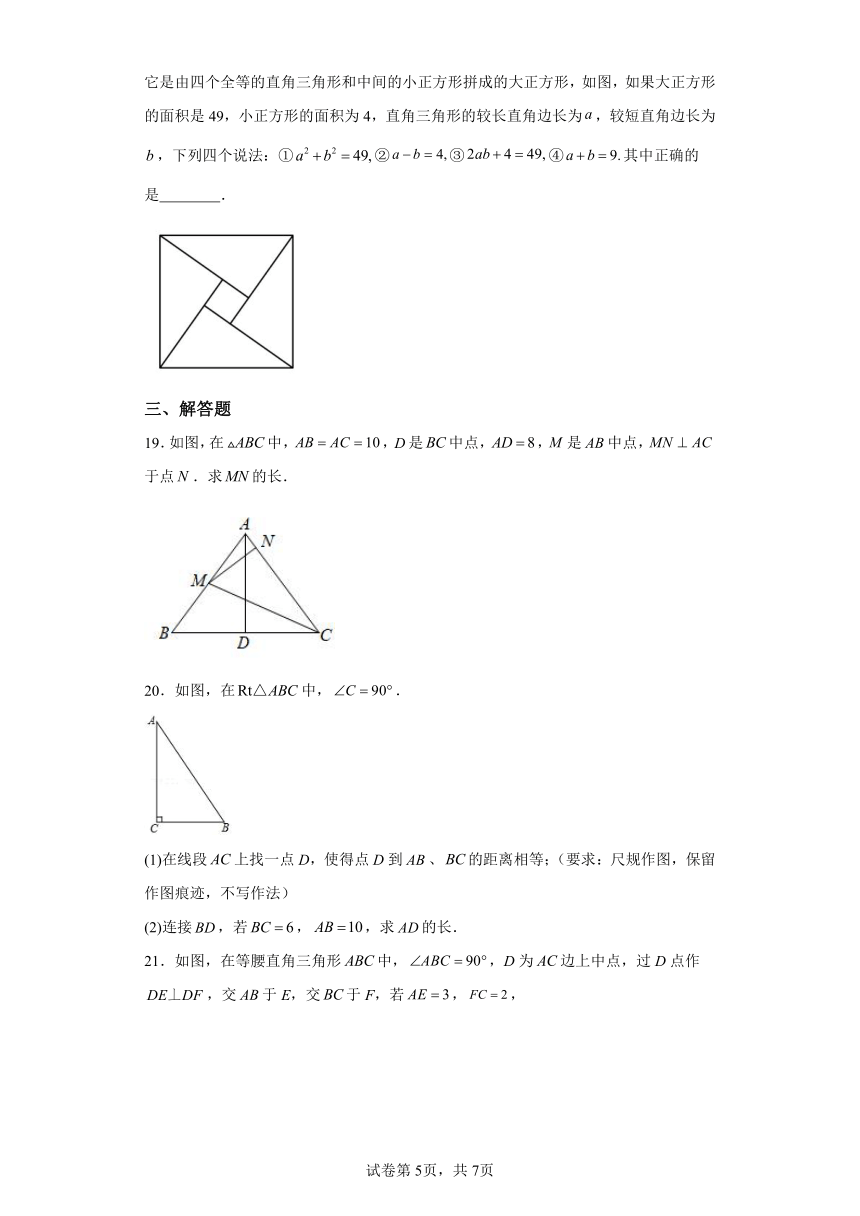
18.2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图,如果大正方形的面积是49,小正方形的面积为4,直角三角形的较长直角边长为,较短直角边长为,下列四个说法:①②③④其中正确的是 .
三、解答题
19.如图,在中,,是中点,,是中点,于点.求的长.
20.如图,在中,.
(1)在线段上找一点D,使得点D到、的距离相等;(要求:尺规作图,保留作图痕迹,不写作法)
(2)连接,若,,求的长.
21.如图,在等腰直角三角形中,,D为边上中点,过D点作,交于E,交于F,若,,
(1)求证;
(2)求长.
22.如图四边形ABCD,,,,、交于点F,E是AD上一点,且.
(1)在1图中找出与相等的角,并证明你的结论
(2)在1图中设与交于点P,连接,探究、、三者之间的关系,并证明.
(3)如图2,若平分,,求的长.
23.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人着迷.
(1)应用场景1—在数轴上画出表示无理数的点.如图1,在数轴上找出表示3的点A,过点A作直线l垂直于OA,在l上取点B,使,以原点O为圆心,OB为半径作弧,则弧与数轴的交点C表示的数是 ;
(2)应用场景2—解决实际问题.如图2,秋千由静止铅锤位置AB推至AC处,它的绳索始终拉直,量得水平距离,求绳索的长.
24.在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
【感知】(1)如图①,当点H与点C重合时,猜想FG与FD的数量关系,并说明理由.
【探究】(2)如图②,当点H为边CD上任意一点时,(1)中结论是否仍然成立?请说明理由.
【应用】(3)在图②中,当DF=3,CE=5时,直接利用探究的结论,求AB的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据勾股数的定义(凡是可以构成一个直角三角形三边的一组正整数,称之为勾股数.)及勾股定理的逆定理计算判断即可.
【详解】A.因为,所以3,4,7不是勾股数;
B.因为,所以7,24,25是勾股数;
C.因为,所以,,不是勾股数;
D.因为勾股数不能为负数,所以3,-4,5不是勾股数;
故选B.
【点睛】本题考查了勾股定理的逆定理,灵活运用平方差公式计算是解题的关键.
2.C
【分析】利用勾股定理计算判断.
【详解】∵点,
∴点到原点的距离是=,
故选C.
【点睛】本题考查了点到原点的距离,熟练运用勾股定理是解题的关键.
3.A
【分析】先利用30度角所对的直角边等于斜边一半,得到,再利用勾股定理即可得到的长.
【详解】解:,,,
,
在中,,
故选:A.
【点睛】本题考查了30度角所对的直角边等于斜边一半,勾股定理,熟练掌握相关知识点是解题关键.
4.B
【分析】延长到点,使得,连接,根据勾股定理的逆定理可得为等腰直角三角形,即可求解.
【详解】解:延长到点,使得,连接,如下图:
由勾股定理得:,,,
∴,,
∴为等腰直角三角形,
∴,
∴,
故选:B.
【点睛】此题考查了勾股定理,勾股定理的逆定理,三角形外角的性质,解题的关键是利用相关性质,构造出等腰直角三角形,正确进行求解.
5.D
【分析】在Rt△ABD及Rt△ADC中可分别表示出BD2及CD2,在Rt△BDM及Rt△CDM中分别将BD2及CD2的表示形式代入表示出BM2和MC2,然后作差即可得出结果.
【详解】解:在Rt△ABD和Rt△ADC中,
BD2=AB2 AD2,CD2=AC2 AD2,
在Rt△BDM和Rt△CDM中,
BM2=BD2+MD2=AB2 AD2+MD2,MC2=CD2+MD2=AC2 AD2+MD2,
∴MC2 MB2=(AC2 AD2+MD2) (AB2 AD2+MD2)
=AC2 AB2
=45.
故选:D.
【点睛】本题考查了勾股定理的知识,题目有一定的技巧性,比较新颖,解答本题需要认真观察,分别两次运用勾股定理求出MC2和MB2是本题的难点,重点还是在于勾股定理的熟练掌握.
6.A
【分析】作A关于河的对称点E,连接,连接,则就是所求的最短距离,利用勾股定理求出的长即可.
【详解】解:作A关于河的对称点E,连接,连接,则就是所求的最短距离.
过A作于G,过E作于F,
∵,
∴,
,
在中, ,
∴铺水管的最短长度是,
故选A.
【点睛】本题主要考查了轴对称最短路径问题,勾股定理,正确作出辅助线是解题的关键.
7.D
【分析】先根据角平分线的性质得到,然后计算,根据勾股定理即可得答案.
【详解】解:∵平分,,,
∴,
∴,
∴,
故选:D.
【点睛】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
8.A
【分析】运用勾股定理可知,每两个相邻的正方形面积和都等于中间斜放的正方形面积,据此即可解答.
【详解】解:如图,观察发现,
∵,
∴,,
∴,
在与中,,
∴(AAS),
∴,
∵,
∴,
即,
同理,,
则,
则.
故选:A.
【点睛】此题考查了全等三角形的判定以及性质、勾股定理.解决本题的关键是得到.
9.B
【分析】根据等腰三角形的性质得到,根据等式的性质得到,求得,根据勾股定理列方程即可得到结论.
【详解】解:∵,
∴,
∵,
∴,
∴,,
∴,
∵,
∴,
∴,
∵,
∴,
在中,根据勾股定理可得:,
∴,
∴,
故选:B.
【点睛】此题参考直角三角形的性质,等腰三角形的性质,勾股定理,证得是解题的关键.
10.D
【分析】根据面积公式推理论证判断即可.
【详解】∵中,根据面积关系,得到
,
∴选项A能证明勾股定理;
∵中,根据面积关系,得到
,
故,
∴选项B能证明勾股定理;
∵中,根据面积关系,得到
,
故,
∴选项C能证明勾股定理;
∵中,根据面积关系,得到
,
∴选项D不能证明勾股定理;
故选:D.
【点睛】本题考查了勾股定理的证明,完全平方公式,熟练掌握勾股定理的证明和完全平方公式的几何意义是解题的关键.
11.4.8##
【分析】根据勾股定理可求出斜边.然后由于同一三角形面积一定,可列方程直接解答.
【详解】解∶直角三角形的两条直角边分别为,
斜边为,
设斜边上的高为,
则直角三角形的面积为,
解得∶,
这个直角三角形斜边上的高为.
故答案为∶.
【点睛】本题考查了勾股定理的运用以及直角三角形的面积的求法,正确利用三角形面积得出其高的长是解题关键.
12.
【分析】过点D作于点H,根据角平分线的定义和性质求得, ,再由直角三角形中所对的边等于斜边的一半以及勾股定理求得,,,最后求得的面积.
【详解】解:如图,过点D作于点H,
,,
,
平分,
,,
,
,
,
.
故答案为:.
【点睛】本题考查了直角三角形的性质和勾股定理,还考查了角平分线的定义和性质,解决本题的关键是掌握相关的性质定理并能灵活运用.
13.48
【分析】由该三角形的周长为24,斜边长为10可知a+b+10=24,再根据勾股定理和完全平方公式即可求出ab的值.
【详解】解:∵三角形的周长为24,斜边长为10,
∴a+b+10=24,
∴a+b=14,
∵a、b是直角三角形的两条直角边,
∴a2+b2=102,
则a2+b2=(a+b)2 2ab=102,
即142 2ab=102,
∴ab=48.
故答案为:48.
【点睛】本题主要考查了勾股定理,掌握利用勾股定理证明线段的平方关系及完全平方公式的变形求值是解题的关键.
14.
【分析】设正方形A,B,C,D的边长依次为a,b,c,d,邻近A的正方形边长为e,邻近D的正方形边长为f,最大正方形的边长为g,根据正方形的面积公式和勾股定理依次计算即可.
【详解】如图,设正方形A,B,C,D的边长依次为a,b,c,d,邻近A的正方形边长为e,邻近D的正方形边长为f,最大正方形的边长为g,且a=3,b=5,c=2,d=3,所有的三角形都是直角三角形.
所以,
所以
=
=47,
所以边长为,
故答案为:.
【点睛】本题考查了正方形的面积和勾股定理,熟练掌握勾股定理是解题的关键.
15.
【分析】首先根据全等三角形的判定定理,即可证得,可得,,,可证得,再根据直角三角形的性质可证得,根据三角形的面积公式,即可求得,最后根据勾股定理可求得,据此即可解答.
【详解】解:,
在与中,
,
,,,
,
,
,
,
,
,
,
,
,
点A的坐标为,
故答案为:.
【点睛】本题考查了全等三角形的判定及性质,直角三角形的性质,勾股定理,证得是解决本题的关键.
16.
【分析】将木块表面展开,然后根据两点之间线段最短,用勾股定理计算解答即可.
【详解】解:如图,将木块展开,得到如图的长方形,
木块的主视图的高是1米的等腰直角三角形,
等腰直角三角形的斜边长为,
等腰直角三角形的直角边长为:,
则图中长方形的长的长为:,宽仍然为3.
于是最短路径为:.
故答案为:.
【点睛】本题主要考查了两点之间线段最短,勾股定理,将木块表面展开,正确得到蚂蚁从点A处到点C处需要走的最短路程的等价距离是关键.
17. 2 3
【分析】利用勾股定理可求出,即可得到,再根据是整数及,由此可求出n的值的个数.
【详解】由题意得
;
;
;
∵,
∴的值是整数,
∴·的值可以是,,
是整数的有3个.
故答案为:2,,3.
【点睛】本题考查了勾股定理的应用;探索图形规律,找到规律是解题的关键.
18.①③##③①
【分析】分别求出小正方形及大正方形的边长,然后根据面积关系得出a与b的关系式,依次判断所给关系式即可.
【详解】解∶由题意可得小正方形的边长,大正方形的边长,故可得,即②错误;
等于大正方形斜边的平方=大正方形的面积,即①正确;
小正方形的面积四个直角三角形的面积等于大正方形的面积,即可得,即③正确;
根据③可得,故可得,从而可得,即④错误.
综上可得①③正确,
故答案为∶①③
【点睛】本题考查了勾股定理及直角三角形的知识,根据所给图形,利用面积关系判断a与b的关系是解答本题的关键.
19.
【分析】根据等腰三角形的性质,得出,,根据勾股定理求出,得出,求出,根据是中点,得出,根据三角形面积公式,即可求出.
【详解】解:∵在中,,是中点,
∴,,
∴,
∴,
∴,
∴,
∵是中点,
∴,
∴,
∵,
∴,
即,
解得:.
【点睛】本题主要考查了等腰三角形的性质,勾股定理,三角形面积的计算,解题的关键是根据中线的性质,求出.
20.(1)见解析
(2)5
【分析】(1)用尺规作出的平分线,交于点D,即可得出答案;
(2)作于点H,证明,得出,求出,根据勾股定理求出,设,
则,根据勾股定理列出关于x的方程,求出x的值,即可得出答案.
【详解】(1)解:点D即为所求;
(2)解:如图,作于点H,
在和中,
,
∴,
∴,
∴,
∵在中,,
∴,
设,
∴,
在中,,
即,
解得,
∴.
【点睛】本题主要考查了尺规作一个角的平分线,三角形全等的判定和性质,勾股定理,解题的关键是作出辅助线,构造全等三角形,利用勾股定理列出方程.
21.(1)见解析;
(2).
【分析】(1)连接,根据的等腰直角三角形的性质证明就可以得出;
(2)由,就可以求得的长.
【详解】(1)证明:如图,连接,
∵D是中点,
∴,,,
∵,,
∴,
在和中,
∴,
∴;
(2)解:∵,,
∴,
在中,.
【点睛】此题考查了全等三角形的判定与性质,勾股定理,解题的关键是熟练掌握相关基本性质.
22.(1),过程见解析
(2),证明见解析
(3)
【分析】(1)根据直角三角形的两个锐角互余即可得出答案;
(2)先截取,再根据“”证明≌,可得,,再根据等腰直角三角形的性质得,进而得出答案;
(3)先根据等腰直角三角形的性质得,再根据角平分线的定义和平行线的性质得,,可得,然后根据“等角对等边”得,接下来结合“”证明≌,可得,再根据勾股定理求出,进而求出,最后根据勾股定理得出答案.
【详解】(1)∵,,
∴.
∵,
∴,,
∴;
(2).
如图,在上截取.
在和中,
∴≌,
∴,.
∵,
∴.
在中,,
即.
∴;
(3)∵,,
∴.
∵平分,
∴.
∵,
∴,,
∴,
∴,
∴.
在中,,
∴,,
∴.
∴,
∴,.
∵,
∴≌,
∴.
在中,,
即,
解得,
∴.
在中,,
即.
【点睛】本题主要考查了全等三角形的性质和判定,等腰三角形的性质和判定,勾股定理,平行线的性质,直角三角形的性质等,构造全等三角形是解题的关键.
23.(1)
(2)绳索AC的长为
【分析】(1)根据勾股定理求出,根据实数与数轴解答即可.
(2)设秋千的绳索长为xm,根据题意可得,利用勾股定理可得,即可得到结论.
【详解】(1)在中,OB===,
∴,
∴点C表示的数是,
故答案为:;
(2)解:设秋千绳索AC的长度为,
由题意可得AC=AB=,
∵,
∴,
在中,,
∴,
解得,
即AC的长度为,
答:绳索AC的长为.
【点睛】本题主要考查了勾股定理的应用,关键是正确理解题意,表示出AD,AC的长,掌握直角三角形中两直角边的平方和等于斜边的平方.
24.[感知] FG=FD,理由见解析;
[探究]成立,理由见解析;
[应用] .
【分析】[感知]运用折叠的性质可证明△AGF≌△ADF,从而得到FG=FD;
[探究] 运用折叠的性质可证明△AGF≌△ADF,从而得到FG=FD;
[应用] 由[探究]中的结论,可设AB=x,则FC=x-3,FE=x,然后在Rt△ECF中,根据勾股定理求解即可.
【详解】[感知]猜想:FG=FD.
证明:如图所示:
连接AF,
由折叠的性质可得AB=AG=AD,
在Rt△AGF和Rt△ADF中,
,
∴△AGF≌△ADF,
故可得FG=FD;
[探究] 当点H为边CD上任意一点时,(1)中结论仍然成立.
证明:如图所示:
连接AF,
由折叠的性质可得AB=AG=AD,
在Rt△AGF和Rt△ADF中,
,
∴△AGF≌△ADF.
∴FG=FD,
故当点H为边CD上任意一点时,(1)中的结论仍然成立;
[应用]设AB=x,则FC=x-3,FE=x,
在Rt△ECF中,EF2=FC2+EC2,即x2=(x-3)2+52,
解得x=.
即AB的长为.
【点睛】折叠的性质和勾股定理及直角三角形全等的判定是本题的考点,熟练运用折叠性质证明△AGF≌△ADF是解题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.下列各组数中,是勾股数的是( )
A.3,4,7 B.7,24,25 C.,, D.3,-4,5
2.平面直角坐标系内,点到原点的距离是( )
A.2 B.3 C. D.2或3
3.如图,在直角三角形中,,,,则( )
A.6 B. C.4 D.
4.如图,正方形网格中,每一小格的边长为1.网格内有,则的度数是( )
A. B. C. D.
5.如图,在△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A.29 B.32 C.36 D.45
6.如图,要在河边l上修建一个水泵站,分别向A村和B村送水,已知A村、B村到河边的距离分别1km和3km,且相距3km,则铺水管的最短长度是( )km
A.5 B.4 C.3 D.6
7.如图,在中,,平分,于,,,则的长为( )
A.6 B.5 C.4 D.3
8.如图,在直线m上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是3,6,9,正放置的四个正方形的面积依次是,,,,则=( )
A.6 B.6.5 C.7 D.8
9.如图,中,,是等腰三角形,,,交于E,,则的值为( )
A.7 B. C.8 D.
10.我国是最早了解勾股定理的国家之一.据《周髀算经》记载,勾股定理的公式与证明是在商代由商高发现的,故又称之为“商高定理”;三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释,并给出了另外一个证明,下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
二、填空题
11.直角三角形的两直角边分别为和,则斜边上的高为 cm.
12.如图,中,,,平分交于点D,,则 的面积为 .
13.设,是直角三角形的两条直角边长,若该三角形的周长为24,斜边长为10,则的值为 .
14.如图是一株美丽的勾股数,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的边长是 .
15.如图所示,点A、B分别是坐标轴上的点,且,轴,点D在x轴负半轴上,,连接OC、BD相交于点E,若四边形ACED的面积为,OE长为1,则点A的坐标为 .
16.在一个长为,宽为3的长方形草地上,如图摆放着一根三棱柱的木块,它的侧棱EF平行于AD,且棱长大于场地宽AD,木块的主视图为等腰直角三角形,且底边上的高为1,一只蚂蚁从点A处到C处需要走的最短路程是 .
17.如图所示,图甲是第七届国际数学教育大会(ICME)的会徽,主体图案是由如图乙的一连串直角三角形演化而成,其中,现把图乙中的直角三角形继续作下去,则 , ;若的值是整数,且,则符合条件的有 个.
18.2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图,如果大正方形的面积是49,小正方形的面积为4,直角三角形的较长直角边长为,较短直角边长为,下列四个说法:①②③④其中正确的是 .
三、解答题
19.如图,在中,,是中点,,是中点,于点.求的长.
20.如图,在中,.
(1)在线段上找一点D,使得点D到、的距离相等;(要求:尺规作图,保留作图痕迹,不写作法)
(2)连接,若,,求的长.
21.如图,在等腰直角三角形中,,D为边上中点,过D点作,交于E,交于F,若,,
(1)求证;
(2)求长.
22.如图四边形ABCD,,,,、交于点F,E是AD上一点,且.
(1)在1图中找出与相等的角,并证明你的结论
(2)在1图中设与交于点P,连接,探究、、三者之间的关系,并证明.
(3)如图2,若平分,,求的长.
23.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人着迷.
(1)应用场景1—在数轴上画出表示无理数的点.如图1,在数轴上找出表示3的点A,过点A作直线l垂直于OA,在l上取点B,使,以原点O为圆心,OB为半径作弧,则弧与数轴的交点C表示的数是 ;
(2)应用场景2—解决实际问题.如图2,秋千由静止铅锤位置AB推至AC处,它的绳索始终拉直,量得水平距离,求绳索的长.
24.在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
【感知】(1)如图①,当点H与点C重合时,猜想FG与FD的数量关系,并说明理由.
【探究】(2)如图②,当点H为边CD上任意一点时,(1)中结论是否仍然成立?请说明理由.
【应用】(3)在图②中,当DF=3,CE=5时,直接利用探究的结论,求AB的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据勾股数的定义(凡是可以构成一个直角三角形三边的一组正整数,称之为勾股数.)及勾股定理的逆定理计算判断即可.
【详解】A.因为,所以3,4,7不是勾股数;
B.因为,所以7,24,25是勾股数;
C.因为,所以,,不是勾股数;
D.因为勾股数不能为负数,所以3,-4,5不是勾股数;
故选B.
【点睛】本题考查了勾股定理的逆定理,灵活运用平方差公式计算是解题的关键.
2.C
【分析】利用勾股定理计算判断.
【详解】∵点,
∴点到原点的距离是=,
故选C.
【点睛】本题考查了点到原点的距离,熟练运用勾股定理是解题的关键.
3.A
【分析】先利用30度角所对的直角边等于斜边一半,得到,再利用勾股定理即可得到的长.
【详解】解:,,,
,
在中,,
故选:A.
【点睛】本题考查了30度角所对的直角边等于斜边一半,勾股定理,熟练掌握相关知识点是解题关键.
4.B
【分析】延长到点,使得,连接,根据勾股定理的逆定理可得为等腰直角三角形,即可求解.
【详解】解:延长到点,使得,连接,如下图:
由勾股定理得:,,,
∴,,
∴为等腰直角三角形,
∴,
∴,
故选:B.
【点睛】此题考查了勾股定理,勾股定理的逆定理,三角形外角的性质,解题的关键是利用相关性质,构造出等腰直角三角形,正确进行求解.
5.D
【分析】在Rt△ABD及Rt△ADC中可分别表示出BD2及CD2,在Rt△BDM及Rt△CDM中分别将BD2及CD2的表示形式代入表示出BM2和MC2,然后作差即可得出结果.
【详解】解:在Rt△ABD和Rt△ADC中,
BD2=AB2 AD2,CD2=AC2 AD2,
在Rt△BDM和Rt△CDM中,
BM2=BD2+MD2=AB2 AD2+MD2,MC2=CD2+MD2=AC2 AD2+MD2,
∴MC2 MB2=(AC2 AD2+MD2) (AB2 AD2+MD2)
=AC2 AB2
=45.
故选:D.
【点睛】本题考查了勾股定理的知识,题目有一定的技巧性,比较新颖,解答本题需要认真观察,分别两次运用勾股定理求出MC2和MB2是本题的难点,重点还是在于勾股定理的熟练掌握.
6.A
【分析】作A关于河的对称点E,连接,连接,则就是所求的最短距离,利用勾股定理求出的长即可.
【详解】解:作A关于河的对称点E,连接,连接,则就是所求的最短距离.
过A作于G,过E作于F,
∵,
∴,
,
在中, ,
∴铺水管的最短长度是,
故选A.
【点睛】本题主要考查了轴对称最短路径问题,勾股定理,正确作出辅助线是解题的关键.
7.D
【分析】先根据角平分线的性质得到,然后计算,根据勾股定理即可得答案.
【详解】解:∵平分,,,
∴,
∴,
∴,
故选:D.
【点睛】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
8.A
【分析】运用勾股定理可知,每两个相邻的正方形面积和都等于中间斜放的正方形面积,据此即可解答.
【详解】解:如图,观察发现,
∵,
∴,,
∴,
在与中,,
∴(AAS),
∴,
∵,
∴,
即,
同理,,
则,
则.
故选:A.
【点睛】此题考查了全等三角形的判定以及性质、勾股定理.解决本题的关键是得到.
9.B
【分析】根据等腰三角形的性质得到,根据等式的性质得到,求得,根据勾股定理列方程即可得到结论.
【详解】解:∵,
∴,
∵,
∴,
∴,,
∴,
∵,
∴,
∴,
∵,
∴,
在中,根据勾股定理可得:,
∴,
∴,
故选:B.
【点睛】此题参考直角三角形的性质,等腰三角形的性质,勾股定理,证得是解题的关键.
10.D
【分析】根据面积公式推理论证判断即可.
【详解】∵中,根据面积关系,得到
,
∴选项A能证明勾股定理;
∵中,根据面积关系,得到
,
故,
∴选项B能证明勾股定理;
∵中,根据面积关系,得到
,
故,
∴选项C能证明勾股定理;
∵中,根据面积关系,得到
,
∴选项D不能证明勾股定理;
故选:D.
【点睛】本题考查了勾股定理的证明,完全平方公式,熟练掌握勾股定理的证明和完全平方公式的几何意义是解题的关键.
11.4.8##
【分析】根据勾股定理可求出斜边.然后由于同一三角形面积一定,可列方程直接解答.
【详解】解∶直角三角形的两条直角边分别为,
斜边为,
设斜边上的高为,
则直角三角形的面积为,
解得∶,
这个直角三角形斜边上的高为.
故答案为∶.
【点睛】本题考查了勾股定理的运用以及直角三角形的面积的求法,正确利用三角形面积得出其高的长是解题关键.
12.
【分析】过点D作于点H,根据角平分线的定义和性质求得, ,再由直角三角形中所对的边等于斜边的一半以及勾股定理求得,,,最后求得的面积.
【详解】解:如图,过点D作于点H,
,,
,
平分,
,,
,
,
,
.
故答案为:.
【点睛】本题考查了直角三角形的性质和勾股定理,还考查了角平分线的定义和性质,解决本题的关键是掌握相关的性质定理并能灵活运用.
13.48
【分析】由该三角形的周长为24,斜边长为10可知a+b+10=24,再根据勾股定理和完全平方公式即可求出ab的值.
【详解】解:∵三角形的周长为24,斜边长为10,
∴a+b+10=24,
∴a+b=14,
∵a、b是直角三角形的两条直角边,
∴a2+b2=102,
则a2+b2=(a+b)2 2ab=102,
即142 2ab=102,
∴ab=48.
故答案为:48.
【点睛】本题主要考查了勾股定理,掌握利用勾股定理证明线段的平方关系及完全平方公式的变形求值是解题的关键.
14.
【分析】设正方形A,B,C,D的边长依次为a,b,c,d,邻近A的正方形边长为e,邻近D的正方形边长为f,最大正方形的边长为g,根据正方形的面积公式和勾股定理依次计算即可.
【详解】如图,设正方形A,B,C,D的边长依次为a,b,c,d,邻近A的正方形边长为e,邻近D的正方形边长为f,最大正方形的边长为g,且a=3,b=5,c=2,d=3,所有的三角形都是直角三角形.
所以,
所以
=
=47,
所以边长为,
故答案为:.
【点睛】本题考查了正方形的面积和勾股定理,熟练掌握勾股定理是解题的关键.
15.
【分析】首先根据全等三角形的判定定理,即可证得,可得,,,可证得,再根据直角三角形的性质可证得,根据三角形的面积公式,即可求得,最后根据勾股定理可求得,据此即可解答.
【详解】解:,
在与中,
,
,,,
,
,
,
,
,
,
,
,
,
点A的坐标为,
故答案为:.
【点睛】本题考查了全等三角形的判定及性质,直角三角形的性质,勾股定理,证得是解决本题的关键.
16.
【分析】将木块表面展开,然后根据两点之间线段最短,用勾股定理计算解答即可.
【详解】解:如图,将木块展开,得到如图的长方形,
木块的主视图的高是1米的等腰直角三角形,
等腰直角三角形的斜边长为,
等腰直角三角形的直角边长为:,
则图中长方形的长的长为:,宽仍然为3.
于是最短路径为:.
故答案为:.
【点睛】本题主要考查了两点之间线段最短,勾股定理,将木块表面展开,正确得到蚂蚁从点A处到点C处需要走的最短路程的等价距离是关键.
17. 2 3
【分析】利用勾股定理可求出,即可得到,再根据是整数及,由此可求出n的值的个数.
【详解】由题意得
;
;
;
∵,
∴的值是整数,
∴·的值可以是,,
是整数的有3个.
故答案为:2,,3.
【点睛】本题考查了勾股定理的应用;探索图形规律,找到规律是解题的关键.
18.①③##③①
【分析】分别求出小正方形及大正方形的边长,然后根据面积关系得出a与b的关系式,依次判断所给关系式即可.
【详解】解∶由题意可得小正方形的边长,大正方形的边长,故可得,即②错误;
等于大正方形斜边的平方=大正方形的面积,即①正确;
小正方形的面积四个直角三角形的面积等于大正方形的面积,即可得,即③正确;
根据③可得,故可得,从而可得,即④错误.
综上可得①③正确,
故答案为∶①③
【点睛】本题考查了勾股定理及直角三角形的知识,根据所给图形,利用面积关系判断a与b的关系是解答本题的关键.
19.
【分析】根据等腰三角形的性质,得出,,根据勾股定理求出,得出,求出,根据是中点,得出,根据三角形面积公式,即可求出.
【详解】解:∵在中,,是中点,
∴,,
∴,
∴,
∴,
∴,
∵是中点,
∴,
∴,
∵,
∴,
即,
解得:.
【点睛】本题主要考查了等腰三角形的性质,勾股定理,三角形面积的计算,解题的关键是根据中线的性质,求出.
20.(1)见解析
(2)5
【分析】(1)用尺规作出的平分线,交于点D,即可得出答案;
(2)作于点H,证明,得出,求出,根据勾股定理求出,设,
则,根据勾股定理列出关于x的方程,求出x的值,即可得出答案.
【详解】(1)解:点D即为所求;
(2)解:如图,作于点H,
在和中,
,
∴,
∴,
∴,
∵在中,,
∴,
设,
∴,
在中,,
即,
解得,
∴.
【点睛】本题主要考查了尺规作一个角的平分线,三角形全等的判定和性质,勾股定理,解题的关键是作出辅助线,构造全等三角形,利用勾股定理列出方程.
21.(1)见解析;
(2).
【分析】(1)连接,根据的等腰直角三角形的性质证明就可以得出;
(2)由,就可以求得的长.
【详解】(1)证明:如图,连接,
∵D是中点,
∴,,,
∵,,
∴,
在和中,
∴,
∴;
(2)解:∵,,
∴,
在中,.
【点睛】此题考查了全等三角形的判定与性质,勾股定理,解题的关键是熟练掌握相关基本性质.
22.(1),过程见解析
(2),证明见解析
(3)
【分析】(1)根据直角三角形的两个锐角互余即可得出答案;
(2)先截取,再根据“”证明≌,可得,,再根据等腰直角三角形的性质得,进而得出答案;
(3)先根据等腰直角三角形的性质得,再根据角平分线的定义和平行线的性质得,,可得,然后根据“等角对等边”得,接下来结合“”证明≌,可得,再根据勾股定理求出,进而求出,最后根据勾股定理得出答案.
【详解】(1)∵,,
∴.
∵,
∴,,
∴;
(2).
如图,在上截取.
在和中,
∴≌,
∴,.
∵,
∴.
在中,,
即.
∴;
(3)∵,,
∴.
∵平分,
∴.
∵,
∴,,
∴,
∴,
∴.
在中,,
∴,,
∴.
∴,
∴,.
∵,
∴≌,
∴.
在中,,
即,
解得,
∴.
在中,,
即.
【点睛】本题主要考查了全等三角形的性质和判定,等腰三角形的性质和判定,勾股定理,平行线的性质,直角三角形的性质等,构造全等三角形是解题的关键.
23.(1)
(2)绳索AC的长为
【分析】(1)根据勾股定理求出,根据实数与数轴解答即可.
(2)设秋千的绳索长为xm,根据题意可得,利用勾股定理可得,即可得到结论.
【详解】(1)在中,OB===,
∴,
∴点C表示的数是,
故答案为:;
(2)解:设秋千绳索AC的长度为,
由题意可得AC=AB=,
∵,
∴,
在中,,
∴,
解得,
即AC的长度为,
答:绳索AC的长为.
【点睛】本题主要考查了勾股定理的应用,关键是正确理解题意,表示出AD,AC的长,掌握直角三角形中两直角边的平方和等于斜边的平方.
24.[感知] FG=FD,理由见解析;
[探究]成立,理由见解析;
[应用] .
【分析】[感知]运用折叠的性质可证明△AGF≌△ADF,从而得到FG=FD;
[探究] 运用折叠的性质可证明△AGF≌△ADF,从而得到FG=FD;
[应用] 由[探究]中的结论,可设AB=x,则FC=x-3,FE=x,然后在Rt△ECF中,根据勾股定理求解即可.
【详解】[感知]猜想:FG=FD.
证明:如图所示:
连接AF,
由折叠的性质可得AB=AG=AD,
在Rt△AGF和Rt△ADF中,
,
∴△AGF≌△ADF,
故可得FG=FD;
[探究] 当点H为边CD上任意一点时,(1)中结论仍然成立.
证明:如图所示:
连接AF,
由折叠的性质可得AB=AG=AD,
在Rt△AGF和Rt△ADF中,
,
∴△AGF≌△ADF.
∴FG=FD,
故当点H为边CD上任意一点时,(1)中的结论仍然成立;
[应用]设AB=x,则FC=x-3,FE=x,
在Rt△ECF中,EF2=FC2+EC2,即x2=(x-3)2+52,
解得x=.
即AB的长为.
【点睛】折叠的性质和勾股定理及直角三角形全等的判定是本题的考点,熟练运用折叠性质证明△AGF≌△ADF是解题的关键.
答案第1页,共2页
答案第1页,共2页
