专题17.4勾股定理的应用 基础篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题17.4勾股定理的应用 基础篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 22:36:29 | ||
图片预览

文档简介
专题17.4 勾股定理的应用(基础篇)(专项练习)
一、单选题
1.一架长的梯子斜靠在墙上,梯子底端到墙的距离为.若梯子顶端下滑,那么梯子底端在水平方向上滑动了( )
A. B.小于 C.大于 D.无法确定
2.如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
A.8米 B.9米 C.10米 D.12米
3.如图是一圆柱玻璃杯,从内部测得底面半径为,高为,现有一根长为的吸管任意放入杯中,则吸管露在杯口外的长度最少是( )
A. B. C. D.
4.如图,原来从A村到B村,需要沿路A→C→B()绕过两地间的一片湖,在A, B间建好桥后,就可直接从A村到B村.已知,,那么,建好桥后从 A村到B村比原来减少的路程为( )
A.2km B.4km C.10 km D.14 km
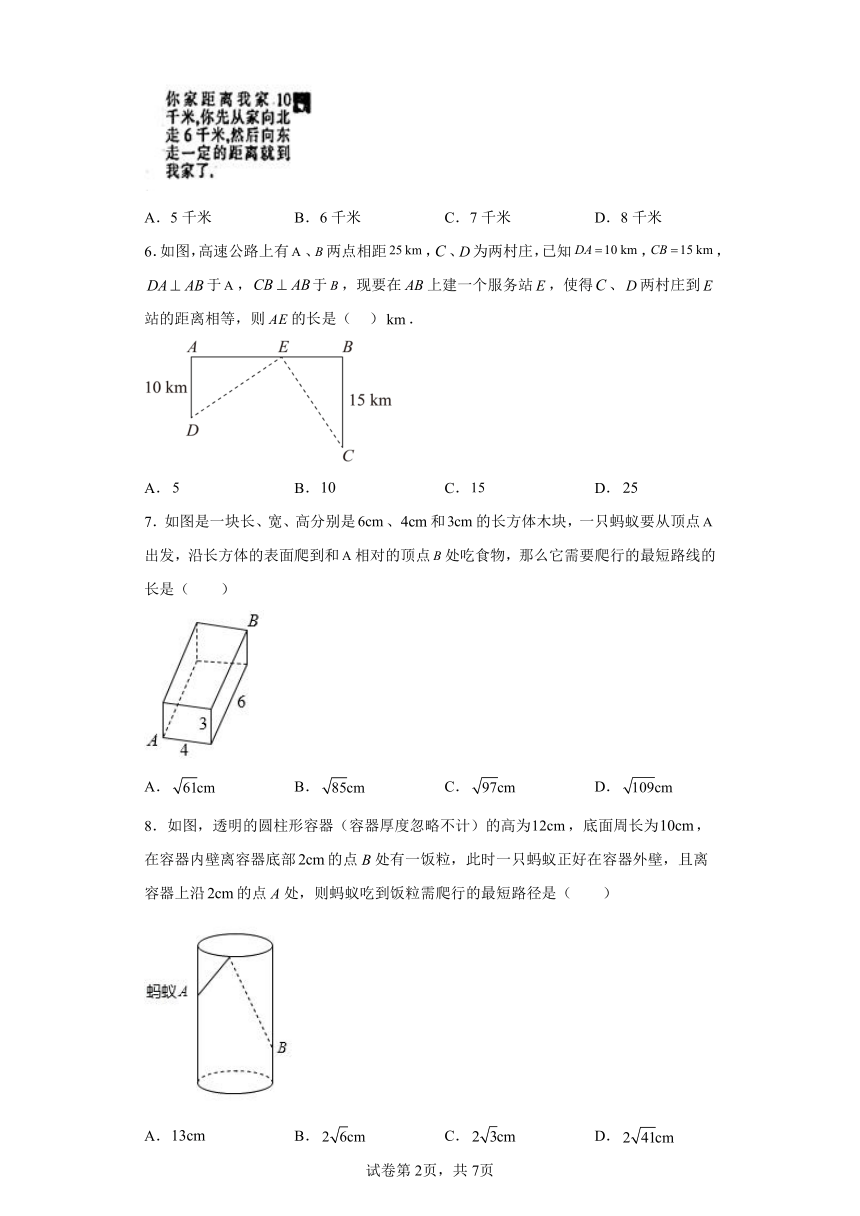
5.如图所示的是小杰使用微信告诉小宇从小宇家到小杰家的方式.根据小杰所说的,最后应向东走( )
A.5千米 B.6千米 C.7千米 D.8千米
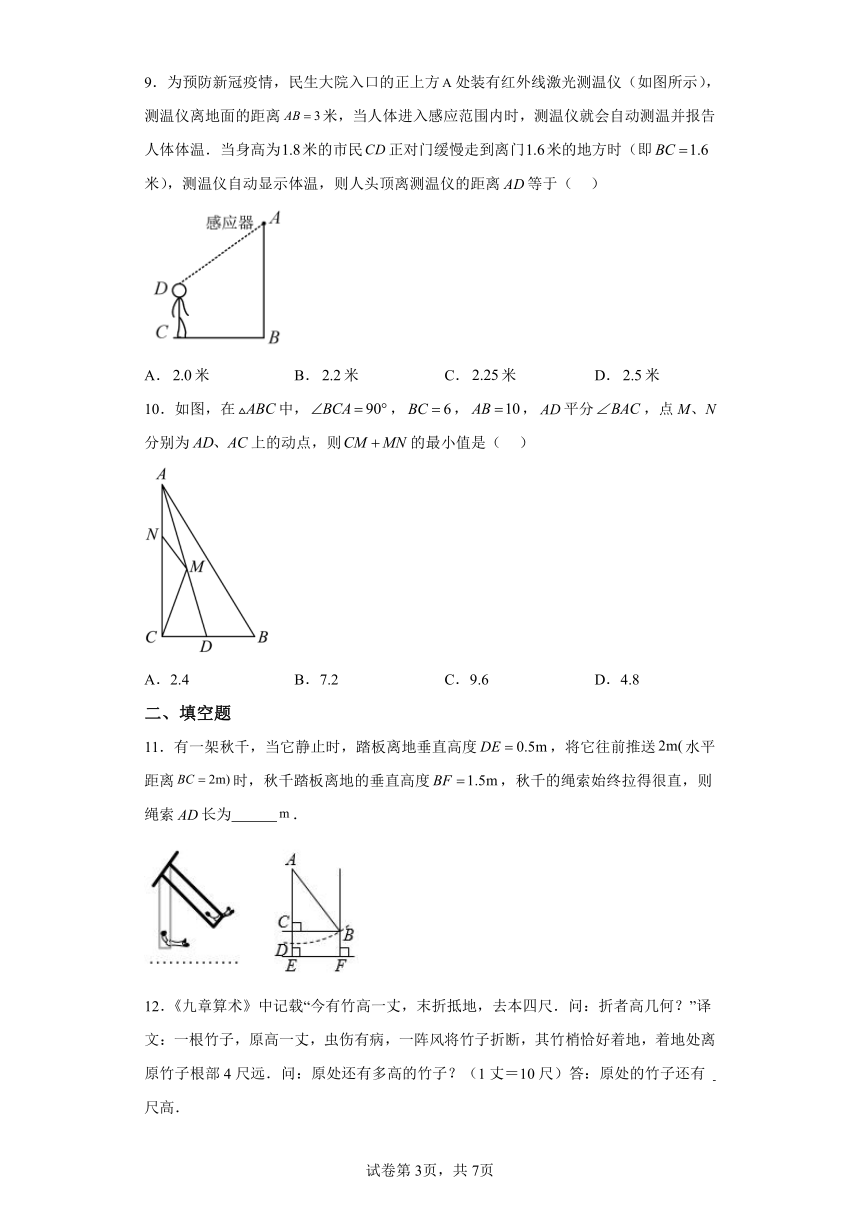
6.如图,高速公路上有、两点相距,、为两村庄,已知,,于,于,现要在上建一个服务站,使得、两村庄到站的距离相等,则的长是( ).
A. B. C. D.
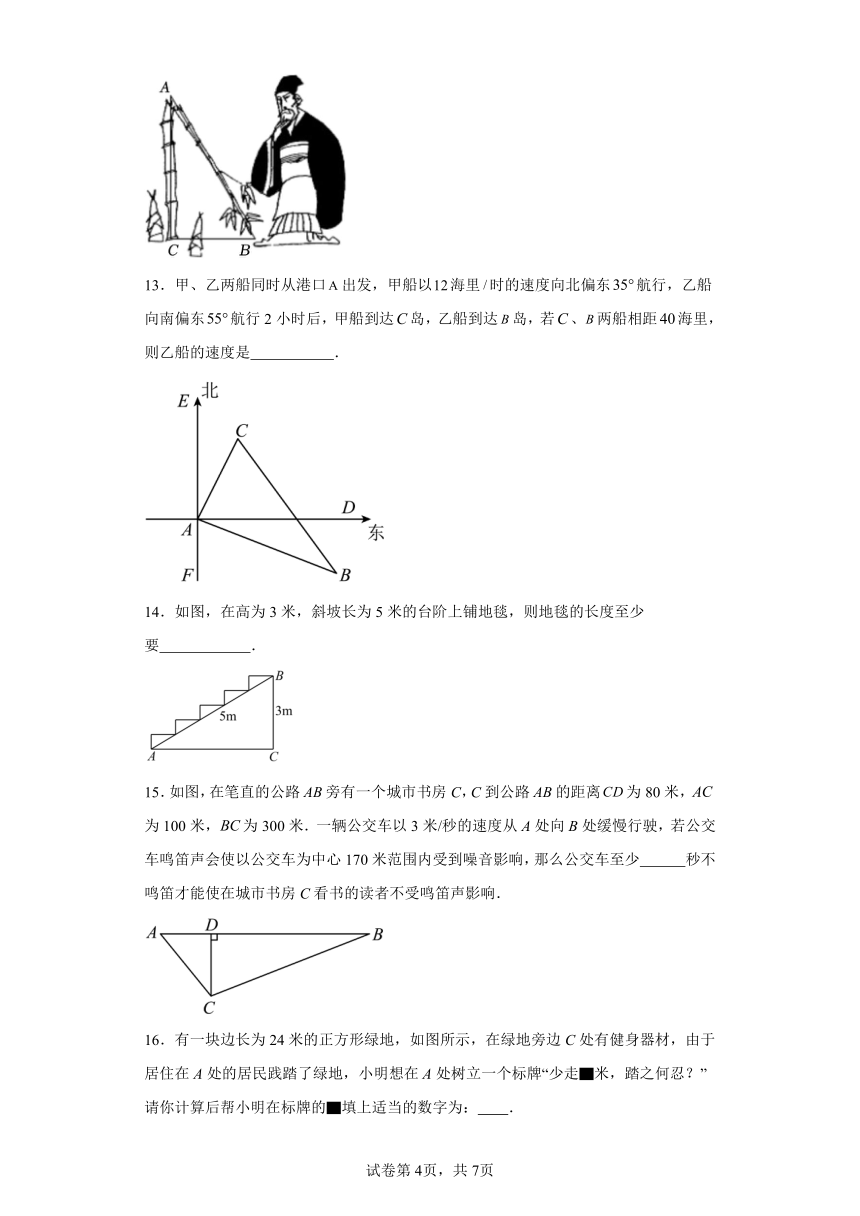
7.如图是一块长、宽、高分别是、和的长方体木块,一只蚂蚁要从顶点出发,沿长方体的表面爬到和相对的顶点处吃食物,那么它需要爬行的最短路线的长是( )
A. B. C. D.
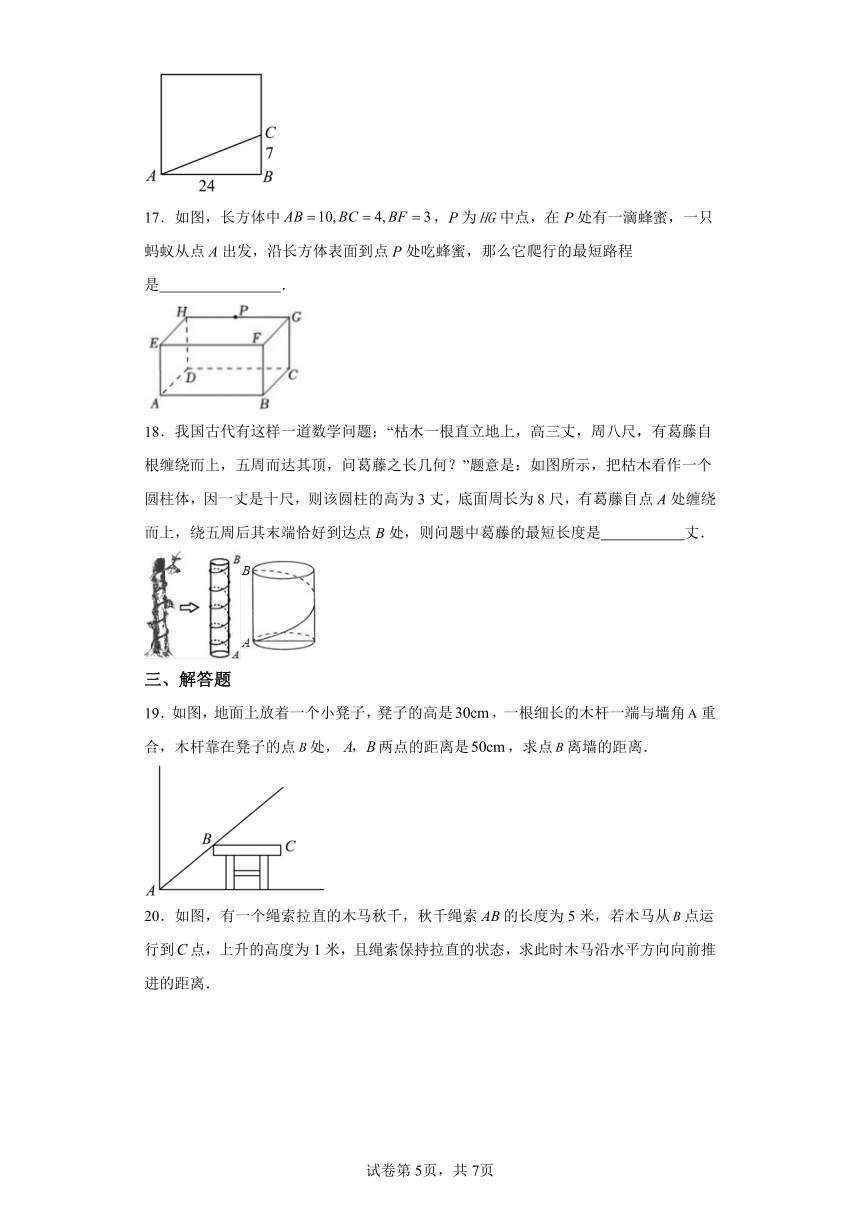
8.如图,透明的圆柱形容器(容器厚度忽略不计)的高为,底面周长为,在容器内壁离容器底部的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
A. B. C. D.
9.为预防新冠疫情,民生大院入口的正上方处装有红外线激光测温仪(如图所示),测温仪离地面的距离米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为米的市民正对门缓慢走到离门米的地方时(即米),测温仪自动显示体温,则人头顶离测温仪的距离等于( )
A.米 B.米 C.米 D.米
10.如图,在中,,,,平分,点M、N分别为上的动点,则的最小值是( )
A.2.4 B.7.2 C.9.6 D.4.8
二、填空题
11.有一架秋千,当它静止时,踏板离地垂直高度,将它往前推送水平距离时,秋千踏板离地的垂直高度,秋千的绳索始终拉得很直,则绳索长为 .
12.《九章算术》中记载“今有竹高一丈,末折抵地,去本四尺.问:折者高几何?”译文:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部4尺远.问:原处还有多高的竹子?(1丈=10尺)答:原处的竹子还有 尺高.
13.甲、乙两船同时从港口出发,甲船以海里时的速度向北偏东航行,乙船向南偏东航行2小时后,甲船到达岛,乙船到达岛,若、两船相距海里,则乙船的速度是 .
14.如图,在高为3米,斜坡长为5米的台阶上铺地毯,则地毯的长度至少要 .
15.如图,在笔直的公路旁有一个城市书房C,C到公路的距离为80米,为100米,为300米.一辆公交车以3米/秒的速度从A处向B处缓慢行驶,若公交车鸣笛声会使以公交车为中心170米范围内受到噪音影响,那么公交车至少 秒不鸣笛才能使在城市书房C看书的读者不受鸣笛声影响.
16.有一块边长为24米的正方形绿地,如图所示,在绿地旁边C处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处树立一个标牌“少走▇米,踏之何忍?”请你计算后帮小明在标牌的▇填上适当的数字为: .
17.如图,长方体中,P为中点,在P处有一滴蜂蜜,一只蚂蚁从点A出发,沿长方体表面到点P处吃蜂蜜,那么它爬行的最短路程是 .
18.我国古代有这样一道数学问题:“枯木一根直立地上,高三丈,周八尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为3丈,底面周长为8尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 丈.
三、解答题
19.如图,地面上放着一个小凳子,凳子的高是,一根细长的木杆一端与墙角重合,木杆靠在凳子的点处,两点的距离是,求点离墙的距离.
20.如图,有一个绳索拉直的木马秋千,秋千绳索的长度为5米,若木马从点运行到点,上升的高度为1米,且绳索保持拉直的状态,求此时木马沿水平方向向前推进的距离.
21.某市创建文明城市,采用移动宣讲的形式进行宣传动员,如图,笔直公路的一侧点处有一学校,学校到公路的距离米,若宣讲车周围800米以内能听到广播宣传,宣讲车在公路上延到的方向行驶时.
(1)请问学校能否听到宣传,请说明理由.
(2)如果能听到,已知宣讲车的速度是256米分,求学校总共能听到多长时间的宣传.
22.如图,某电信公司计划在,两乡镇间的处修建一座信号塔,且使,两个村庄到的距离相等.已知于点,于点,,,,求信号塔应该建在离乡镇多少千米的地方?
23.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几.”(注:1步=5尺)
译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,问绳索有多长.”
24.勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法,证法如下:
把两个全等的直角三角形(Rt△ABC≌Rt△DAE)如图1放置,∠DAB=∠B=90°,AC⊥DE于点F,点E在边AB上,现设Rt△ACB两直角边长分别为CB=b、BA=a,斜边长为AC=c,请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理
(1)请根据上述图形的面积关系证明勾股定理;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,CD为两个村庄(看作直线上的两点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为多少千米.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据题意作图,利用勾股定理即可求解.
【详解】解:根据题意作图如下,
由题意知,,,
,
,
,
,
梯子底端在水平方向上滑动的距离是.
故选A.
【点睛】本题主要考查勾股定理,解题的关键是根据题意作图分析求解.
2.C
【分析】根据勾股定理解答即可.
【详解】如图:由题意可得AB=10-4=6米,BC=6米,
AC==10米.
故选:C.
【点睛】此题主要考查了勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
3.B
【分析】根据底面半径求得直径为,根据勾股定理求得吸管在杯子中的最大长度,进而即可求解.
【详解】解:∵底面半径为,则直径为,高为,
∴吸管露在杯口外的长度最少为:.
故选:B.
【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题的关键.
4.B
【分析】直接利用勾股定理得出的长,进而得出答案.
【详解】解:由题意可得:
则打通隧道后从A村到B村比原来减少的路程为:(km).
故选:B.
【点睛】此题主要考查了勾股定理的应用,正确得出的长是解题关键.
5.D
【分析】通过题干给出的信息,画出简图,发现小宇走了6千米之后此时的位置与小宇家和小杰家构成了直角三角形,利用直角三角形的勾股定理解答.
【详解】
由图可知:小宇向北走6km后,小杰的家在小宇的正东方向.
此时可以运用勾股定理得,向东走的距离为:(km).
故应选:D.
【点睛】本题考查了直角三角形的实际应用,解题关键在于,充分理解题干信息,画出简图进行分析.
6.C
【分析】根据题意设出的长为,再由勾股定理列出方程求解即可.
【详解】解:设,则,
由勾股定理得:
在中,
,
在中,
,
由题意可知:,
所以:,
解得:.
所以,应建在距点处.
故选:.
【点睛】本题考查正确运用勾股定理,善于观察题目的信息是解题以及学好数学的关键.
7.B
【分析】分三种情况讨论即可,然后利用勾股定理即可求得最短线段的长,再比较三种情况下最短的线段即可得到答案.
【详解】第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是和,
则所走的最短线段是;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是和,
所以走的最短线段是;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是和,
所以走的最短线段是;
因为,
所以第二种情况最短.
故选:B.
【点睛】本题主要考查的是平面展开——最短路径问题,解决此题的关键是明确线段最短这一知识点,然后把长方体的一些面展开到一个平面内,求出最短的线段.
8.A
【分析】将容器侧面展开,建立A关于的对称点,根据两点之间线段最短可知的长度即为所求.
【详解】解:如图:
∵高为,底面周长为,在容器内壁离容器底部的点B处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿与饭粒相对的点A处,
∴,
∴将容器侧面展开,作A关于的对称点,
连接,则即为最短距离,
,
故选:A.
【点睛】本题考查了平面展开—最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.
9.A
【分析】过点作于点,根据题意求得,在中,勾股定理即可求解.
【详解】解:如图,过点作于点,
∴,,
在中,
故选:A.
【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题的关键.
10.D
【分析】取点N关于的对称点E,由轴对称图形或成轴对称的性质可推出,从而得到,当点C、M、E在一条直线上且时,有最小值,最后利用等面积法求得的值即得.
【详解】解:取点N关于的对称点E,如下图:
∵平分
∴点E在上
∵点N与点E关于对称
∴是N点与E点所连线段的垂直平分线
∴
∴
当时,CE有最小值,即有最小值
∵在中,,,
∴
∵在中,
∴
∴
∴最小值为.
故选:D.
【点睛】本题考查最短路径问题、轴对称图形或成轴对称的性质、角平分线的性质及等面积法,对称转化是解决最短路径问题的常用方法,本题解题关键是将最短路径问题转化为垂线段最短的问题.
11.
【分析】设秋千的绳索长为,根据题意可得,利用勾股定理可得,再解方程即可得出答案.
【详解】解:在中,
,
设秋千的绳索长为,
则,
故,
解得:,
答:绳索AD的长度是.
故答案为:.
【点睛】此题主要考查了勾股定理的应用,关键是正确理解题意,表示出的长,掌握直角三角形中两直角边的平方和等于斜边的平方.
12.
【分析】竹子折断后刚好构成一直角三角形,设竹子折断处离地面x尺,则斜边为尺.利用勾股定理解题即可.
【详解】解:设竹子折断处离地面x尺,则斜边为尺,
根据勾股定理得:,
解得:.
故答案是:.
【点睛】此题考查了勾股定理的应用,解题的关键是利用题目信息构造直角三角形,从而运用勾股定理解题.
13.海里时
【分析】根据已知判定为直角,根据路程公式求得的长.再根据勾股定理求得的长,从而根据公式求得其速度.
【详解】解:甲的速度是海里时,时间是小时,
海里.
,
.
海里,
海里.
乙船也用小时,
乙船的速度是海里时.
故答案为:海里时.
【点睛】此题考查了直角三角形的判定及方向角的掌握情况,关键是根据勾股定理求得的长.
14.米##7m
【分析】先求出AC的长,再利用平移的知识即可得出地毯的长度.
【详解】在 Rt△ABC中,∠C=90°,AB=5,BC=3,
∴AC==4(米),
∴可得地毯长度=AC+BC=7(米),
故答案为:米.
【点睛】本题考查了勾股定理的应用及平移的知识,利用由平移得到地毯长度是AC+BC的长是解答本题的关键.
15.70
【分析】如图,设米,由勾股定理求出和的长,则可求出答案.
【详解】解:如图,设米,
∵,米,
∴(米),
∵米,米,
∴(米),
∴(米),
∴公交车鸣笛声会受到噪音影响的时间为(秒),
故答案为:70.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
16.6
【分析】先根据勾股定理求出斜边AC的长,比较即可得到结果.
【详解】,
米,
答:标牌的▇处应填6.
考点:本题考查的是勾股定理的应用
【点睛】此题主要考查学生对勾股定理在实际生活中的运用能力,同时也增强了学生们要爱护草地的意识.
17.
【分析】根据长方体展开图画出图形,利用勾股定理求出的长即可.
【详解】解:如图1,
如图2
.
【点睛】此题主要考查了平面展开图的最短路径问题和勾股定理的应用,画出图形是解题关键.
18.5
【分析】根据题意画出图形,在Rt中,再根据勾股定理求解即可.
【详解】如图所示:表示葛藤的最短长度,
由题意可知:
(丈),(丈),
在Rt中,
(丈).
故答案为:5.
【点睛】本题考查了平面展开—最短路径问题,能够根据题意画出图形,构造直角三角形是解题的关键.
19.
【分析】过作地面于点,在中,由勾股定理求出的长即可.
【详解】解:如图,过作地面于点,
则,
由题意得:,
在中,由勾股定理得:,
答:点离墙的距离为.
【点睛】本题考查了勾股定理的应用,理解题意,正确作出辅助线构造直角三角形是解题的关键.
20.3米
【分析】过点C作于点F,由题意得米,米,则米,再由勾股定理求出CF的长即可.
【详解】解:如图所示,过点C作于点F,
根据题意得:米,米,
所以(米),
由勾股定理可得,
所以,
所以(米),
所以木马向前推进的长度为3米.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
21.(1)学校能听到宣传,见解析
(2)分钟
【分析】(1)根据学校到公路的距离为480米米,于是得到结论;
(2)根据勾股定理得到米,求得米,于是得到结论.
【详解】(1)解:学校能听到宣传,
理由:学校到公路的距离为480米米,
学校能听到宣传;
(2)如图:假设当宣讲车行驶到点开始影响学校,行驶点结束对学校的影响,
则米,米,
(米),
米,
影响学校的时间为:(分钟),
学校总共能听到分钟的宣传.
【点睛】本题考查了点到直线的距离,勾股定理的应用,掌握勾股定理是解题的关键.
22.
【分析】设,则,根据勾股定理可得,,,结合得到关于x的方程,求解即可.
【详解】解:设,则,
∵,,
∴和都是直角三角形,
在中,
,
在中,
,
∵,,,
∴,
解得,
答:信号塔应该建在距离A乡镇的地方.
【点睛】本题考查了勾股定理的实际应用,根据题意列出方程是解题的关键.
23.尺
【分析】设秋千的绳索长为x尺,根据题意可得AB=(x-4)尺,利用勾股定理可得x2=102+(x-4)2,解之即可.
【详解】解:设秋千的绳索长为x尺,根据题意可列方程为:
x2=102+(x-4)2,
解得:x=,
∴秋千的绳索长为尺.
【点睛】此题主要考查了勾股定理的应用,关键是正确理解题意,表示出AB、AC的长,掌握直角三角形中两直角边的平方和等于斜边的平方.
24.(1)见解析
(2)两个村庄相距41千米.
【分析】(1)根据三角形的面积和梯形的面积就可表示出.
(2)连接CD,作CE⊥AD于点E,根据AD⊥AB,BC⊥AB得到BC=AE,CE=AB,从而得到DE=AD-AE=24-16=8千米,利用勾股定理求得CD两地之间的距离.
【详解】(1)解:∵S梯形ABCD=a(a+b),S△EBC=b(a-b),S四边形AECD=c2,
它们满足的关系式为:a(a+b)=b(a-b)+c2,
即a2+b2=c2;
(2)解:如图2①,连接CD,作CE⊥AD于点E,
∵AD⊥AB,BC⊥AB,
∴BC=AE,CE=AB,
∴DE=AD-AE=25-16=9千米,
∴CD= =41(千米),
∴两个村庄相距41千米.
【点睛】此题主要考查了梯形,证明勾股定理,勾股定理的应用,证明勾股定理常用的方法是利用面积证明,是解本题的关键.构造出直角三角形DEF是解本题的难点.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.一架长的梯子斜靠在墙上,梯子底端到墙的距离为.若梯子顶端下滑,那么梯子底端在水平方向上滑动了( )
A. B.小于 C.大于 D.无法确定
2.如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
A.8米 B.9米 C.10米 D.12米
3.如图是一圆柱玻璃杯,从内部测得底面半径为,高为,现有一根长为的吸管任意放入杯中,则吸管露在杯口外的长度最少是( )
A. B. C. D.
4.如图,原来从A村到B村,需要沿路A→C→B()绕过两地间的一片湖,在A, B间建好桥后,就可直接从A村到B村.已知,,那么,建好桥后从 A村到B村比原来减少的路程为( )
A.2km B.4km C.10 km D.14 km
5.如图所示的是小杰使用微信告诉小宇从小宇家到小杰家的方式.根据小杰所说的,最后应向东走( )
A.5千米 B.6千米 C.7千米 D.8千米
6.如图,高速公路上有、两点相距,、为两村庄,已知,,于,于,现要在上建一个服务站,使得、两村庄到站的距离相等,则的长是( ).
A. B. C. D.
7.如图是一块长、宽、高分别是、和的长方体木块,一只蚂蚁要从顶点出发,沿长方体的表面爬到和相对的顶点处吃食物,那么它需要爬行的最短路线的长是( )
A. B. C. D.
8.如图,透明的圆柱形容器(容器厚度忽略不计)的高为,底面周长为,在容器内壁离容器底部的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
A. B. C. D.
9.为预防新冠疫情,民生大院入口的正上方处装有红外线激光测温仪(如图所示),测温仪离地面的距离米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为米的市民正对门缓慢走到离门米的地方时(即米),测温仪自动显示体温,则人头顶离测温仪的距离等于( )
A.米 B.米 C.米 D.米
10.如图,在中,,,,平分,点M、N分别为上的动点,则的最小值是( )
A.2.4 B.7.2 C.9.6 D.4.8
二、填空题
11.有一架秋千,当它静止时,踏板离地垂直高度,将它往前推送水平距离时,秋千踏板离地的垂直高度,秋千的绳索始终拉得很直,则绳索长为 .
12.《九章算术》中记载“今有竹高一丈,末折抵地,去本四尺.问:折者高几何?”译文:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部4尺远.问:原处还有多高的竹子?(1丈=10尺)答:原处的竹子还有 尺高.
13.甲、乙两船同时从港口出发,甲船以海里时的速度向北偏东航行,乙船向南偏东航行2小时后,甲船到达岛,乙船到达岛,若、两船相距海里,则乙船的速度是 .
14.如图,在高为3米,斜坡长为5米的台阶上铺地毯,则地毯的长度至少要 .
15.如图,在笔直的公路旁有一个城市书房C,C到公路的距离为80米,为100米,为300米.一辆公交车以3米/秒的速度从A处向B处缓慢行驶,若公交车鸣笛声会使以公交车为中心170米范围内受到噪音影响,那么公交车至少 秒不鸣笛才能使在城市书房C看书的读者不受鸣笛声影响.
16.有一块边长为24米的正方形绿地,如图所示,在绿地旁边C处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处树立一个标牌“少走▇米,踏之何忍?”请你计算后帮小明在标牌的▇填上适当的数字为: .
17.如图,长方体中,P为中点,在P处有一滴蜂蜜,一只蚂蚁从点A出发,沿长方体表面到点P处吃蜂蜜,那么它爬行的最短路程是 .
18.我国古代有这样一道数学问题:“枯木一根直立地上,高三丈,周八尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为3丈,底面周长为8尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 丈.
三、解答题
19.如图,地面上放着一个小凳子,凳子的高是,一根细长的木杆一端与墙角重合,木杆靠在凳子的点处,两点的距离是,求点离墙的距离.
20.如图,有一个绳索拉直的木马秋千,秋千绳索的长度为5米,若木马从点运行到点,上升的高度为1米,且绳索保持拉直的状态,求此时木马沿水平方向向前推进的距离.
21.某市创建文明城市,采用移动宣讲的形式进行宣传动员,如图,笔直公路的一侧点处有一学校,学校到公路的距离米,若宣讲车周围800米以内能听到广播宣传,宣讲车在公路上延到的方向行驶时.
(1)请问学校能否听到宣传,请说明理由.
(2)如果能听到,已知宣讲车的速度是256米分,求学校总共能听到多长时间的宣传.
22.如图,某电信公司计划在,两乡镇间的处修建一座信号塔,且使,两个村庄到的距离相等.已知于点,于点,,,,求信号塔应该建在离乡镇多少千米的地方?
23.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几.”(注:1步=5尺)
译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,问绳索有多长.”
24.勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法,证法如下:
把两个全等的直角三角形(Rt△ABC≌Rt△DAE)如图1放置,∠DAB=∠B=90°,AC⊥DE于点F,点E在边AB上,现设Rt△ACB两直角边长分别为CB=b、BA=a,斜边长为AC=c,请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理
(1)请根据上述图形的面积关系证明勾股定理;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,CD为两个村庄(看作直线上的两点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为多少千米.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据题意作图,利用勾股定理即可求解.
【详解】解:根据题意作图如下,
由题意知,,,
,
,
,
,
梯子底端在水平方向上滑动的距离是.
故选A.
【点睛】本题主要考查勾股定理,解题的关键是根据题意作图分析求解.
2.C
【分析】根据勾股定理解答即可.
【详解】如图:由题意可得AB=10-4=6米,BC=6米,
AC==10米.
故选:C.
【点睛】此题主要考查了勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
3.B
【分析】根据底面半径求得直径为,根据勾股定理求得吸管在杯子中的最大长度,进而即可求解.
【详解】解:∵底面半径为,则直径为,高为,
∴吸管露在杯口外的长度最少为:.
故选:B.
【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题的关键.
4.B
【分析】直接利用勾股定理得出的长,进而得出答案.
【详解】解:由题意可得:
则打通隧道后从A村到B村比原来减少的路程为:(km).
故选:B.
【点睛】此题主要考查了勾股定理的应用,正确得出的长是解题关键.
5.D
【分析】通过题干给出的信息,画出简图,发现小宇走了6千米之后此时的位置与小宇家和小杰家构成了直角三角形,利用直角三角形的勾股定理解答.
【详解】
由图可知:小宇向北走6km后,小杰的家在小宇的正东方向.
此时可以运用勾股定理得,向东走的距离为:(km).
故应选:D.
【点睛】本题考查了直角三角形的实际应用,解题关键在于,充分理解题干信息,画出简图进行分析.
6.C
【分析】根据题意设出的长为,再由勾股定理列出方程求解即可.
【详解】解:设,则,
由勾股定理得:
在中,
,
在中,
,
由题意可知:,
所以:,
解得:.
所以,应建在距点处.
故选:.
【点睛】本题考查正确运用勾股定理,善于观察题目的信息是解题以及学好数学的关键.
7.B
【分析】分三种情况讨论即可,然后利用勾股定理即可求得最短线段的长,再比较三种情况下最短的线段即可得到答案.
【详解】第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是和,
则所走的最短线段是;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是和,
所以走的最短线段是;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是和,
所以走的最短线段是;
因为,
所以第二种情况最短.
故选:B.
【点睛】本题主要考查的是平面展开——最短路径问题,解决此题的关键是明确线段最短这一知识点,然后把长方体的一些面展开到一个平面内,求出最短的线段.
8.A
【分析】将容器侧面展开,建立A关于的对称点,根据两点之间线段最短可知的长度即为所求.
【详解】解:如图:
∵高为,底面周长为,在容器内壁离容器底部的点B处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿与饭粒相对的点A处,
∴,
∴将容器侧面展开,作A关于的对称点,
连接,则即为最短距离,
,
故选:A.
【点睛】本题考查了平面展开—最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.
9.A
【分析】过点作于点,根据题意求得,在中,勾股定理即可求解.
【详解】解:如图,过点作于点,
∴,,
在中,
故选:A.
【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题的关键.
10.D
【分析】取点N关于的对称点E,由轴对称图形或成轴对称的性质可推出,从而得到,当点C、M、E在一条直线上且时,有最小值,最后利用等面积法求得的值即得.
【详解】解:取点N关于的对称点E,如下图:
∵平分
∴点E在上
∵点N与点E关于对称
∴是N点与E点所连线段的垂直平分线
∴
∴
当时,CE有最小值,即有最小值
∵在中,,,
∴
∵在中,
∴
∴
∴最小值为.
故选:D.
【点睛】本题考查最短路径问题、轴对称图形或成轴对称的性质、角平分线的性质及等面积法,对称转化是解决最短路径问题的常用方法,本题解题关键是将最短路径问题转化为垂线段最短的问题.
11.
【分析】设秋千的绳索长为,根据题意可得,利用勾股定理可得,再解方程即可得出答案.
【详解】解:在中,
,
设秋千的绳索长为,
则,
故,
解得:,
答:绳索AD的长度是.
故答案为:.
【点睛】此题主要考查了勾股定理的应用,关键是正确理解题意,表示出的长,掌握直角三角形中两直角边的平方和等于斜边的平方.
12.
【分析】竹子折断后刚好构成一直角三角形,设竹子折断处离地面x尺,则斜边为尺.利用勾股定理解题即可.
【详解】解:设竹子折断处离地面x尺,则斜边为尺,
根据勾股定理得:,
解得:.
故答案是:.
【点睛】此题考查了勾股定理的应用,解题的关键是利用题目信息构造直角三角形,从而运用勾股定理解题.
13.海里时
【分析】根据已知判定为直角,根据路程公式求得的长.再根据勾股定理求得的长,从而根据公式求得其速度.
【详解】解:甲的速度是海里时,时间是小时,
海里.
,
.
海里,
海里.
乙船也用小时,
乙船的速度是海里时.
故答案为:海里时.
【点睛】此题考查了直角三角形的判定及方向角的掌握情况,关键是根据勾股定理求得的长.
14.米##7m
【分析】先求出AC的长,再利用平移的知识即可得出地毯的长度.
【详解】在 Rt△ABC中,∠C=90°,AB=5,BC=3,
∴AC==4(米),
∴可得地毯长度=AC+BC=7(米),
故答案为:米.
【点睛】本题考查了勾股定理的应用及平移的知识,利用由平移得到地毯长度是AC+BC的长是解答本题的关键.
15.70
【分析】如图,设米,由勾股定理求出和的长,则可求出答案.
【详解】解:如图,设米,
∵,米,
∴(米),
∵米,米,
∴(米),
∴(米),
∴公交车鸣笛声会受到噪音影响的时间为(秒),
故答案为:70.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
16.6
【分析】先根据勾股定理求出斜边AC的长,比较即可得到结果.
【详解】,
米,
答:标牌的▇处应填6.
考点:本题考查的是勾股定理的应用
【点睛】此题主要考查学生对勾股定理在实际生活中的运用能力,同时也增强了学生们要爱护草地的意识.
17.
【分析】根据长方体展开图画出图形,利用勾股定理求出的长即可.
【详解】解:如图1,
如图2
.
【点睛】此题主要考查了平面展开图的最短路径问题和勾股定理的应用,画出图形是解题关键.
18.5
【分析】根据题意画出图形,在Rt中,再根据勾股定理求解即可.
【详解】如图所示:表示葛藤的最短长度,
由题意可知:
(丈),(丈),
在Rt中,
(丈).
故答案为:5.
【点睛】本题考查了平面展开—最短路径问题,能够根据题意画出图形,构造直角三角形是解题的关键.
19.
【分析】过作地面于点,在中,由勾股定理求出的长即可.
【详解】解:如图,过作地面于点,
则,
由题意得:,
在中,由勾股定理得:,
答:点离墙的距离为.
【点睛】本题考查了勾股定理的应用,理解题意,正确作出辅助线构造直角三角形是解题的关键.
20.3米
【分析】过点C作于点F,由题意得米,米,则米,再由勾股定理求出CF的长即可.
【详解】解:如图所示,过点C作于点F,
根据题意得:米,米,
所以(米),
由勾股定理可得,
所以,
所以(米),
所以木马向前推进的长度为3米.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
21.(1)学校能听到宣传,见解析
(2)分钟
【分析】(1)根据学校到公路的距离为480米米,于是得到结论;
(2)根据勾股定理得到米,求得米,于是得到结论.
【详解】(1)解:学校能听到宣传,
理由:学校到公路的距离为480米米,
学校能听到宣传;
(2)如图:假设当宣讲车行驶到点开始影响学校,行驶点结束对学校的影响,
则米,米,
(米),
米,
影响学校的时间为:(分钟),
学校总共能听到分钟的宣传.
【点睛】本题考查了点到直线的距离,勾股定理的应用,掌握勾股定理是解题的关键.
22.
【分析】设,则,根据勾股定理可得,,,结合得到关于x的方程,求解即可.
【详解】解:设,则,
∵,,
∴和都是直角三角形,
在中,
,
在中,
,
∵,,,
∴,
解得,
答:信号塔应该建在距离A乡镇的地方.
【点睛】本题考查了勾股定理的实际应用,根据题意列出方程是解题的关键.
23.尺
【分析】设秋千的绳索长为x尺,根据题意可得AB=(x-4)尺,利用勾股定理可得x2=102+(x-4)2,解之即可.
【详解】解:设秋千的绳索长为x尺,根据题意可列方程为:
x2=102+(x-4)2,
解得:x=,
∴秋千的绳索长为尺.
【点睛】此题主要考查了勾股定理的应用,关键是正确理解题意,表示出AB、AC的长,掌握直角三角形中两直角边的平方和等于斜边的平方.
24.(1)见解析
(2)两个村庄相距41千米.
【分析】(1)根据三角形的面积和梯形的面积就可表示出.
(2)连接CD,作CE⊥AD于点E,根据AD⊥AB,BC⊥AB得到BC=AE,CE=AB,从而得到DE=AD-AE=24-16=8千米,利用勾股定理求得CD两地之间的距离.
【详解】(1)解:∵S梯形ABCD=a(a+b),S△EBC=b(a-b),S四边形AECD=c2,
它们满足的关系式为:a(a+b)=b(a-b)+c2,
即a2+b2=c2;
(2)解:如图2①,连接CD,作CE⊥AD于点E,
∵AD⊥AB,BC⊥AB,
∴BC=AE,CE=AB,
∴DE=AD-AE=25-16=9千米,
∴CD= =41(千米),
∴两个村庄相距41千米.
【点睛】此题主要考查了梯形,证明勾股定理,勾股定理的应用,证明勾股定理常用的方法是利用面积证明,是解本题的关键.构造出直角三角形DEF是解本题的难点.
答案第1页,共2页
答案第1页,共2页
