专题17.7勾股定理的逆定理 基础篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题17.7勾股定理的逆定理 基础篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 683.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 22:37:09 | ||
图片预览



文档简介
专题17.7 勾股定理的逆定理(基础篇)(专项练习)
一、单选题
1.以下列各组数作为三边的长,不能围成直角三角形的是( )
A.,, B.,, C.,, D.,,
2.已知一个的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
3.如图,是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是3,4,5,6,9选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A.5,6,9 B.4,5,9 C.3,4,5 D.3,3,6
4.如图所示,小正方形的边长均为1,A、B、C三点均在正方形格点上,则下列结论错误的是( )
A. B.
C.点A到直线的距离为2 D.
5.如图,在四边形ABCD中,AB=2,BC=2,CD=1,DA=3,且∠ABC=90°,则∠BCD的度数是( )
A.90° B.120° C.135° D.150°
6.若三角形的三边长分别为,,,且满足,则此三角形中最大的角是( )
A.锐角 B.直角 C.钝角 D.无法确定
7.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
8.如图,在△ABC中,AD⊥BC于点D,AB=17,BD=15,DC=6,则AC的长为( ).
A.11 B.10 C.9 D.8
9.已知一个三角形三边长分别是4,9,12,要作最长边上的高正确的图形做法是( )
A. B. C. D.
10.如图,在中,,,,和的平分线交于点,则的度数为( )
A. B. C. D.
二、填空题
11.若、、为的三边长,且满足,则是 三角形.
12.如图,在每个小正方形的边长为1的网格中,各顶点均在网格的格点上,于点D,则的长为 .
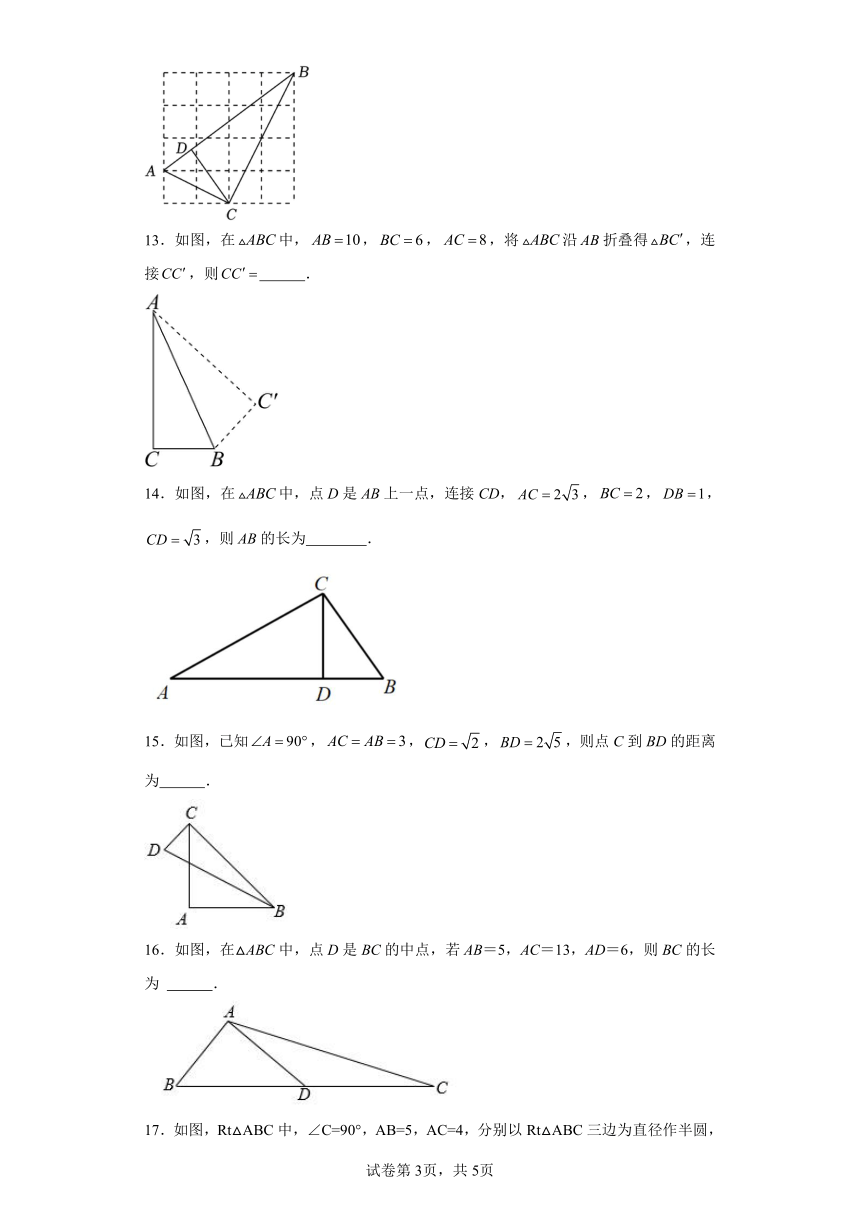
13.如图,在中,,,,将沿折叠得,连接,则 .
14.如图,在中,点D是AB上一点,连接CD,,,,,则AB的长为 .
15.如图,已知,,,,则点C到BD的距离为 .
16.如图,在△ABC中,点D是BC的中点,若AB=5,AC=13,AD=6,则BC的长为 .
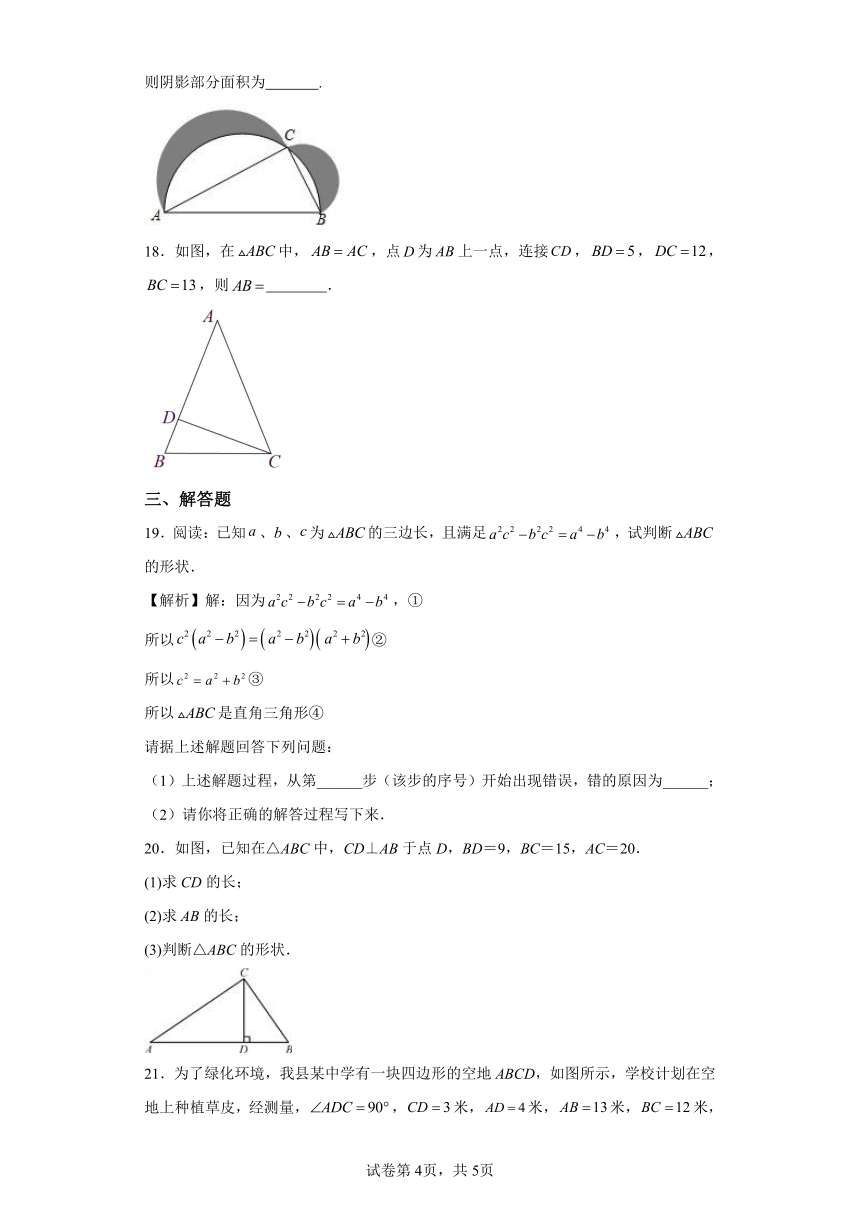
17.如图,Rt△ABC中,∠C=90°,AB=5,AC=4,分别以Rt△ABC三边为直径作半圆,则阴影部分面积为 .
18.如图,在中,,点为上一点,连接,,,,则 .
三、解答题
19.阅读:已知、、为的三边长,且满足,试判断的形状.
【解析】解:因为,①
所以②
所以③
所以是直角三角形④
请据上述解题回答下列问题:
(1)上述解题过程,从第______步(该步的序号)开始出现错误,错的原因为______;
(2)请你将正确的解答过程写下来.
20.如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.
21.为了绿化环境,我县某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量,,米,米,米,米,
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?
22.探究题:如图,在等腰三角形ABC中,AB=AC,其底边长为8 cm,腰长为5 cm,一动点P在底边上从点B出发向点C以0.25 cm/s的速度移动,请你探究:当点P运动多长时间时,点P与顶点A的连线PA与腰垂直.
23.在海洋上有一近似于四边形的岛屿,其平面如图甲,小明据此构造处该岛的一个数学模型(如图乙四边形ABCD),AC是四边形岛屿上的一条小溪流,其中∠B=90°,AB=BC=5千米,千米,千米.
(1)求小溪流AC的长.
(2)求四边形ABCD的面积.(结果保留根号)
24.我市夏季经常收台风天气影响,台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,且km,以台风中心为圆心周围250km以内为受影响区域.
(1)求证:;
(2)海港C受台风影响吗?为什么?
(3)若台风的速度为40km/h,则台风影响该海港持续的时间有多长?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据勾股定理逆定理判断即可.
【详解】解:A.,,
,
,,作为三边的长,能围成直角三角形,
选项正确,不符合题意;
B.,,
,
,,作为三边的长能围成直角三角形,
选项正确,不符合题意;
C.,,
,
,,作为三边的长不能围成直角三角形,
选项错误,符合题意;
D.,,
,
,,作为三边的长能围成直角三角形,
选项正确,不符合题意;
故选C.
【点睛】本题考查了勾股定理的逆定理,熟练掌握勾股定理的逆定理是解题的关键.
2.D
【分析】由于4是三角形的直角边与斜边不能确定,故应分两种情况进行讨论.
【详解】解:由于4是三角形的直角边与斜边不能确定,故应分两种情况进行讨论:
(1)3、4都为直角边,由勾股定理得,斜边为5;
(2)3为直角边,4为斜边,由勾股定理得,直角边为.
∴第三边长的平方是25或7,
故选:D.
【点睛】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
3.B
【分析】根据勾股定理,,则小的两个正方形的面积等于大正方形的面积,再分别进行判断,即可得到面积最大的三角形.
【详解】设三个正方形的边长为:a、b、c(,),且使所围成的三角形是直角三角形,
∴,
A.∵,故不符合题意;
B.∵,∴三角形的面积为:;
C.∵,故不符合题意;
D.∵,∴三角形的面积为:;
∵,
∴,
故选:B
【点睛】本题考查了以直角三角形三边为边长的图形面积和判断三边能否构成直角三角形,以及三角形的面积公式,解题的关键是熟练掌握勾股定理.
4.B
【分析】根据格点及勾股定理可得,,,然后根据勾股定理逆定理及等积法可进行求解.
【详解】解:由图可得:,,,
∴,
∴是直角三角形,即,
∴,
设点A到直线的距离为h,
∴,
∴,
综上可知只有B选项错误;
故选B.
【点睛】本题主要考查勾股定理及其逆定理,熟练掌握勾股定理及其逆定理是解题的关键.
5.C
【分析】连接AC,由于,利用勾股定理可求AC,并可求,而,易得,可证是直角三角形,于是有,从而易求∠BCD.
【详解】解:如图所示,连接AC,
∵,
∴,
又,
∴,
∴,
∴是直角三角形,
∴,
∴.
故选:C.
【点睛】本题考查了等腰三角形的性质,勾股定理,勾股定理的逆定理,解题的关键是连接AC,并证明是直角三角形.
6.B
【分析】因为a、b、c为一个三角形的三边长,化简,可得a2+b2=c2,根据勾股定理的逆定理即可得出该三角形为直角三角形.
【详解】∵,
∴a2+b2=c2,
∴该三角形为直角三角形.
故选B.
【点睛】本题考查勾股定理的逆定理,解题的关键是掌握勾股定理的逆定理.
7.C
【分析】根据勾股定理即可得到AB,BC,AC的长度,进行判断即可.
【详解】解:连接AC,如图:
根据勾股定理可以得到:AC=BC=,AB=.
∵()2+()2=()2.
∴AC2+BC2=AB2.
∴△ABC是等腰直角三角形.
∴∠ABC=45°.
故选C.
【点睛】本题考查了勾股定理的应用,熟练掌握其性质是解题的关键.
8.B
【分析】在直角△ABD中由勾股定理可以求得AD的长度;然后在直角△ACD中,根据勾股定理来求线段AC的长度即可.
【详解】如图,∵AD⊥BC,
∴∠ADB=∠ADC=90°.
又∵AB=17,BD=15,DC=6,
∴在直角△ABD中,由勾股定理得到:AD2=AB2 BD2=64.
在直角△ACD中,由勾股定理得到:AC= =10,即AC=10.
故选B.
【点睛】此题考查勾股定理,解题关键在于掌握运算公式.
9.C
【分析】由三角形的三边为4,9,12,可知该三角形为钝角三角形,其最长边上的高在三角形内部,即过最长边所对的角的顶点,作对边的垂线,垂足在最长边上.
【详解】解:∵42+92=97<122,
∴三角形为钝角三角形,
∴最长边上的高是过最长边所对的角的顶点,作对边的垂线,垂足在最长边上.
故选:C.
【点睛】本题考查了三角形高的画法.当三角形为锐角三角形时,三条高在三角形内部;当三角形是直角三角形时,两条高是三角形的直角边,一条高在三角形内部;当三角形为钝角三角形时,两条高在三角形外部,一条高在内部.
10.A
【分析】根据勾股定理逆定理,可以得出是直角三角形,,根据平分,平分,即可得出答案.
【详解】∵在中,,,,
∴,
∴
∴
∵平分,平分,
∴,
∴
故选A.
【点睛】本题考查了勾股定理逆定理,角平分线的定义,熟练掌握性质灵活运用是本题的关键.
11.直角
【分析】首先根据求出a,b,c的值,然后根据勾股定理的逆定理求解即可.
【详解】∵
∴
∴解得
∵,
∴
∴是直角三角形.
故答案为:直角.
【点睛】本题考查了非负数的性质和勾股定理的逆定理.明确非负数的性质:如果一组非负数的和为0时,则每一个非负数都等于0.
12.2
【分析】由勾股定理可求的长,由勾股定理的逆定理可证,由面积法可求解.
【详解】解:由题意可得:,,,
∵,
∴,
∴,
∵,
∴,
∴,
故答案为:2.
【点睛】本题考查了勾股定理及勾股定理逆定理,三角形的面积公式,证明是解题的关键.
13.
【分析】根据勾股定理逆定理得到,根据翻折性质得出,,然后借助三角形的面积公式列出关于线段CO的关系式,问题即可解决.
【详解】解:如图,连接交于点O,
∵,,,,
∴,
∴,
根据翻折的性质得,,,
∵,
∴,
∴,
故答案为:.
【点睛】此题考查了翻折的性质,熟练掌握翻折的性质是解题的关键.
14.4
【分析】首先在△CDB中,BC2=CD2+DB2,由勾股定理的逆定理得到△CDB为直角三角形,所以∠CDB=90°,在Rt△ADC中由勾股定理可求出AD的值,从而求出AB=AD+DB=4.
【详解】解:在△CDB中,BC2=22=4,CD2+DB2=,
∴ BC2=CD2+DB2,
∴△CDB为直角三角形,
∴∠CDB=90°,
∴∠ADC=90°,
在Rt△ADC中,由勾股定理可得,
∴AB=AD+DB=4.
故答案为:4.
【点睛】本题考查了勾股定理和勾股定理的逆定理,掌握勾股定理和逆定理的应用方法是本题的解题关键.
15.##
【分析】先勾股定理求得,进而勾股定理的逆定理判定是直角三角形,进而根据等面积法求点C到BD的距离.
【详解】解:∵,,
∴
,,
,
是直角三角形
设点C到BD的距离为,则
故答案为:.
【点睛】本题考查了勾股定理及其逆定理,掌握勾股定理是解题的关键.
16.
【分析】延长AD到E,使DE=AD,连接BE.先运用SAS证明△ADC≌△EDB,得出BE=13.再由勾股定理的逆定理证明出∠BAE=90°,然后在△ABD中运用勾股定理求出BD的长,从而得出BC=2BD.
【详解】解:延长AD到E,使DE=AD,连接BE.
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴AC=BE=13.
在△ABE中,AB=5,AE=12,BE=13,
∴AB2+AE2=BE2,
∴∠BAE=90°.
在△ABD中,∠BAD=90°,AB=5,AD=6,
∴BD=,
∴BC=.
故答案为:.
【点睛】本题考查了全等三角形的判定与性质,勾股定理及其逆定理,综合性较强,难度中等.题中延长中线的一倍是常用的辅助线的作法.
17.6
【分析】先利用勾股定理列式求出BC,再根据阴影部分面积等于以AC、BC为直径的两个半圆的面积加上直角三角形ABC的面积减去以AB为直径的半圆的面积,列式计算即可得解.
【详解】解:∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,
∵AB=5,AC=4,
∴,
S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC-直径为AB的半圆的面积
=
=
=
=
=
=6.
【点睛】本题考查了勾股定理,半圆的面积,熟记定理并观察图形表示出阴影部分的面积是解题的关键.
18.
【分析】根据勾股定理的逆定理可得,然后设,则,在中,根据勾股定理,即可求解.
【详解】解:∵,,,
∴,
∴,即,
设,则,
在中,,
∴,
解得:,
即.
故答案为:
【点睛】本题主要考查了勾股定理及其逆定理,根据题意得到是解题的关键.
19.(1)③,忽略了的情况;(2)见解析
【分析】(1)根据题意可直接进行求解;
(2)由因式分解及勾股定理逆定理可直接进行求解.
【详解】解:(1)由题意可得:从第③步开始错误,错的原因为:忽略了的情况;
故答案为③;忽略了的情况;
(2)正确的写法为:
当时,;当时,;
所以是直角三角形或等腰三角形或等腰直角三角形.
【点睛】本题主要考查勾股定理逆定理及因式分解,熟练掌握勾股定理逆定理及因式分解是解题的关键.
20.(1)CD长为12;(2)AB的长为25;(3)△ABC是直角三角形
【详解】解:在△BCD中,∵CD⊥AB,
∴BD2+CD2=BC2
∴CD2=BC2-BD2=152-92=144.
∴CD=12.
(2)在△ACD中,∵CD⊥AB,
∴CD2+AD2=AC2
∴AD2=AC2-CD2=202-122=256.
∴AD=16.
∴AB=AD+BD=16+9=25.
(3)∵BC2+AC2=152+202=625,AB2=252=625,
∴AB2=BC2+AC2
∴△ABC是直角三角形.
21.(1)24平方米;(2)4800元
【分析】(1)连接,在直角三角形中可求得的长,由、、的长度关系可得三角形为一直角三角形,为斜边;由此看,四边形的面积等于面积减的面积解答即可;
(2)根据题意列式计算即可.
【详解】解:(1)连接,
在中,,
在中,,,
而,
即,
,
.
(2)需费用(元),
答:总共需投入4800元.
【点睛】本题考查了勾股定理的应用,通过勾股定理由边与边的关系也可证明直角三角形,这样解题较为简单.
22.当点P运动的时间为7 s或25 s时,点P与顶点A的连线与腰垂直.
【分析】利用勾股定理求出AD的长,再利用勾股定理逆定理即可证明垂直.
【详解】(1)过点A作AD⊥BC于点D.
∵AB=AC,BC=8 cm,
∴BD=CD=BC=4 cm.
由勾股定理,得AD==3(cm).
分两种情况:(1)如图,当点P运动t秒后有PA⊥AC(P在线段BD上)时,
∵AP2=PD2+AD2=PC2-AC2,
∴PD2+32=(PD+4)2-52,∴PD=2.25 cm,
∴BP=4-2.25=1.75,
∴0.25t=1.75,解得t=7.
(2)当点P运动t秒后有PA⊥AB(P在线段CD上)时,同理可得PD=2.25,∴BP=4+2.25=6.25,
∴0.25t=6.25,解得t=25.
综上所述,当点P运动的时间为7 s或25 s时,点P与顶点A的连线与腰垂直.
【点睛】本题考查了勾股定理与勾股定理逆定理的应用,熟悉概念是解题关键.
23.(1)千米;
(2)平方千米
【分析】(1)根据勾股定理已知直角边求斜边计算;
(2)将四边形分成两个三角形,求证为直角,四边形面积为两个直角三角形面积之和.
【详解】(1)解:(1)∵∠B=90°,AB=BC=5千米,
∴(千米);
(2)∵(千米),(千米),(千米),
∴,,,
∴,
∴是直角三角形,则∠D=90°,
∴(平方千米).
【点睛】本题考查了勾股定理及其逆定理的应用,熟练掌握勾股定理的概念和公式并灵活运用是解题关键 .
24.(1)见解析
(2)海港C受台风影响,理由见解析
(3)3.5h
【分析】(1)根据勾股定理的逆定理,即可求解;
(2)过点C作于D.根据直角三角形的面积,可得,即可求解;
(3)在线段AB上取点E,F,使km,km,则台风中心在线段EF上时正好影响C港口.根据等腰三角形的性质可得ED=FD,然后根据勾股定理可得,从而得到km,即可求解.
【详解】(1)解:∵km,km,km,
∴.
∴是直角三角形,
∴;
(2)解:海港C受台风影响.理由如下:
如图,过点C作于D.
∵,
∴.
∵,
∴海港C受到台风影响.
(3)解:如图,在线段AB上取点E,F,使km,km,则台风中心在线段EF上时正好影响C港口.
∴EC=FC,
∵CD⊥AB,
∴ED=FD,
在中,由勾股定理得:
,
∴km,
∵台风的速度为40km/h,
∴.
∴台风影响该海港持续的时间为3.5h .
【点睛】本题主要考查了勾股定理的逆定理,勾股定理的实际应用,等腰三角形的性质,熟练掌握勾股定理的逆定理,正确构造直角三角形是解题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.以下列各组数作为三边的长,不能围成直角三角形的是( )
A.,, B.,, C.,, D.,,
2.已知一个的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
3.如图,是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是3,4,5,6,9选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A.5,6,9 B.4,5,9 C.3,4,5 D.3,3,6
4.如图所示,小正方形的边长均为1,A、B、C三点均在正方形格点上,则下列结论错误的是( )
A. B.
C.点A到直线的距离为2 D.
5.如图,在四边形ABCD中,AB=2,BC=2,CD=1,DA=3,且∠ABC=90°,则∠BCD的度数是( )
A.90° B.120° C.135° D.150°
6.若三角形的三边长分别为,,,且满足,则此三角形中最大的角是( )
A.锐角 B.直角 C.钝角 D.无法确定
7.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
8.如图,在△ABC中,AD⊥BC于点D,AB=17,BD=15,DC=6,则AC的长为( ).
A.11 B.10 C.9 D.8
9.已知一个三角形三边长分别是4,9,12,要作最长边上的高正确的图形做法是( )
A. B. C. D.
10.如图,在中,,,,和的平分线交于点,则的度数为( )
A. B. C. D.
二、填空题
11.若、、为的三边长,且满足,则是 三角形.
12.如图,在每个小正方形的边长为1的网格中,各顶点均在网格的格点上,于点D,则的长为 .
13.如图,在中,,,,将沿折叠得,连接,则 .
14.如图,在中,点D是AB上一点,连接CD,,,,,则AB的长为 .
15.如图,已知,,,,则点C到BD的距离为 .
16.如图,在△ABC中,点D是BC的中点,若AB=5,AC=13,AD=6,则BC的长为 .
17.如图,Rt△ABC中,∠C=90°,AB=5,AC=4,分别以Rt△ABC三边为直径作半圆,则阴影部分面积为 .
18.如图,在中,,点为上一点,连接,,,,则 .
三、解答题
19.阅读:已知、、为的三边长,且满足,试判断的形状.
【解析】解:因为,①
所以②
所以③
所以是直角三角形④
请据上述解题回答下列问题:
(1)上述解题过程,从第______步(该步的序号)开始出现错误,错的原因为______;
(2)请你将正确的解答过程写下来.
20.如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.
21.为了绿化环境,我县某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量,,米,米,米,米,
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?
22.探究题:如图,在等腰三角形ABC中,AB=AC,其底边长为8 cm,腰长为5 cm,一动点P在底边上从点B出发向点C以0.25 cm/s的速度移动,请你探究:当点P运动多长时间时,点P与顶点A的连线PA与腰垂直.
23.在海洋上有一近似于四边形的岛屿,其平面如图甲,小明据此构造处该岛的一个数学模型(如图乙四边形ABCD),AC是四边形岛屿上的一条小溪流,其中∠B=90°,AB=BC=5千米,千米,千米.
(1)求小溪流AC的长.
(2)求四边形ABCD的面积.(结果保留根号)
24.我市夏季经常收台风天气影响,台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,且km,以台风中心为圆心周围250km以内为受影响区域.
(1)求证:;
(2)海港C受台风影响吗?为什么?
(3)若台风的速度为40km/h,则台风影响该海港持续的时间有多长?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据勾股定理逆定理判断即可.
【详解】解:A.,,
,
,,作为三边的长,能围成直角三角形,
选项正确,不符合题意;
B.,,
,
,,作为三边的长能围成直角三角形,
选项正确,不符合题意;
C.,,
,
,,作为三边的长不能围成直角三角形,
选项错误,符合题意;
D.,,
,
,,作为三边的长能围成直角三角形,
选项正确,不符合题意;
故选C.
【点睛】本题考查了勾股定理的逆定理,熟练掌握勾股定理的逆定理是解题的关键.
2.D
【分析】由于4是三角形的直角边与斜边不能确定,故应分两种情况进行讨论.
【详解】解:由于4是三角形的直角边与斜边不能确定,故应分两种情况进行讨论:
(1)3、4都为直角边,由勾股定理得,斜边为5;
(2)3为直角边,4为斜边,由勾股定理得,直角边为.
∴第三边长的平方是25或7,
故选:D.
【点睛】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
3.B
【分析】根据勾股定理,,则小的两个正方形的面积等于大正方形的面积,再分别进行判断,即可得到面积最大的三角形.
【详解】设三个正方形的边长为:a、b、c(,),且使所围成的三角形是直角三角形,
∴,
A.∵,故不符合题意;
B.∵,∴三角形的面积为:;
C.∵,故不符合题意;
D.∵,∴三角形的面积为:;
∵,
∴,
故选:B
【点睛】本题考查了以直角三角形三边为边长的图形面积和判断三边能否构成直角三角形,以及三角形的面积公式,解题的关键是熟练掌握勾股定理.
4.B
【分析】根据格点及勾股定理可得,,,然后根据勾股定理逆定理及等积法可进行求解.
【详解】解:由图可得:,,,
∴,
∴是直角三角形,即,
∴,
设点A到直线的距离为h,
∴,
∴,
综上可知只有B选项错误;
故选B.
【点睛】本题主要考查勾股定理及其逆定理,熟练掌握勾股定理及其逆定理是解题的关键.
5.C
【分析】连接AC,由于,利用勾股定理可求AC,并可求,而,易得,可证是直角三角形,于是有,从而易求∠BCD.
【详解】解:如图所示,连接AC,
∵,
∴,
又,
∴,
∴,
∴是直角三角形,
∴,
∴.
故选:C.
【点睛】本题考查了等腰三角形的性质,勾股定理,勾股定理的逆定理,解题的关键是连接AC,并证明是直角三角形.
6.B
【分析】因为a、b、c为一个三角形的三边长,化简,可得a2+b2=c2,根据勾股定理的逆定理即可得出该三角形为直角三角形.
【详解】∵,
∴a2+b2=c2,
∴该三角形为直角三角形.
故选B.
【点睛】本题考查勾股定理的逆定理,解题的关键是掌握勾股定理的逆定理.
7.C
【分析】根据勾股定理即可得到AB,BC,AC的长度,进行判断即可.
【详解】解:连接AC,如图:
根据勾股定理可以得到:AC=BC=,AB=.
∵()2+()2=()2.
∴AC2+BC2=AB2.
∴△ABC是等腰直角三角形.
∴∠ABC=45°.
故选C.
【点睛】本题考查了勾股定理的应用,熟练掌握其性质是解题的关键.
8.B
【分析】在直角△ABD中由勾股定理可以求得AD的长度;然后在直角△ACD中,根据勾股定理来求线段AC的长度即可.
【详解】如图,∵AD⊥BC,
∴∠ADB=∠ADC=90°.
又∵AB=17,BD=15,DC=6,
∴在直角△ABD中,由勾股定理得到:AD2=AB2 BD2=64.
在直角△ACD中,由勾股定理得到:AC= =10,即AC=10.
故选B.
【点睛】此题考查勾股定理,解题关键在于掌握运算公式.
9.C
【分析】由三角形的三边为4,9,12,可知该三角形为钝角三角形,其最长边上的高在三角形内部,即过最长边所对的角的顶点,作对边的垂线,垂足在最长边上.
【详解】解:∵42+92=97<122,
∴三角形为钝角三角形,
∴最长边上的高是过最长边所对的角的顶点,作对边的垂线,垂足在最长边上.
故选:C.
【点睛】本题考查了三角形高的画法.当三角形为锐角三角形时,三条高在三角形内部;当三角形是直角三角形时,两条高是三角形的直角边,一条高在三角形内部;当三角形为钝角三角形时,两条高在三角形外部,一条高在内部.
10.A
【分析】根据勾股定理逆定理,可以得出是直角三角形,,根据平分,平分,即可得出答案.
【详解】∵在中,,,,
∴,
∴
∴
∵平分,平分,
∴,
∴
故选A.
【点睛】本题考查了勾股定理逆定理,角平分线的定义,熟练掌握性质灵活运用是本题的关键.
11.直角
【分析】首先根据求出a,b,c的值,然后根据勾股定理的逆定理求解即可.
【详解】∵
∴
∴解得
∵,
∴
∴是直角三角形.
故答案为:直角.
【点睛】本题考查了非负数的性质和勾股定理的逆定理.明确非负数的性质:如果一组非负数的和为0时,则每一个非负数都等于0.
12.2
【分析】由勾股定理可求的长,由勾股定理的逆定理可证,由面积法可求解.
【详解】解:由题意可得:,,,
∵,
∴,
∴,
∵,
∴,
∴,
故答案为:2.
【点睛】本题考查了勾股定理及勾股定理逆定理,三角形的面积公式,证明是解题的关键.
13.
【分析】根据勾股定理逆定理得到,根据翻折性质得出,,然后借助三角形的面积公式列出关于线段CO的关系式,问题即可解决.
【详解】解:如图,连接交于点O,
∵,,,,
∴,
∴,
根据翻折的性质得,,,
∵,
∴,
∴,
故答案为:.
【点睛】此题考查了翻折的性质,熟练掌握翻折的性质是解题的关键.
14.4
【分析】首先在△CDB中,BC2=CD2+DB2,由勾股定理的逆定理得到△CDB为直角三角形,所以∠CDB=90°,在Rt△ADC中由勾股定理可求出AD的值,从而求出AB=AD+DB=4.
【详解】解:在△CDB中,BC2=22=4,CD2+DB2=,
∴ BC2=CD2+DB2,
∴△CDB为直角三角形,
∴∠CDB=90°,
∴∠ADC=90°,
在Rt△ADC中,由勾股定理可得,
∴AB=AD+DB=4.
故答案为:4.
【点睛】本题考查了勾股定理和勾股定理的逆定理,掌握勾股定理和逆定理的应用方法是本题的解题关键.
15.##
【分析】先勾股定理求得,进而勾股定理的逆定理判定是直角三角形,进而根据等面积法求点C到BD的距离.
【详解】解:∵,,
∴
,,
,
是直角三角形
设点C到BD的距离为,则
故答案为:.
【点睛】本题考查了勾股定理及其逆定理,掌握勾股定理是解题的关键.
16.
【分析】延长AD到E,使DE=AD,连接BE.先运用SAS证明△ADC≌△EDB,得出BE=13.再由勾股定理的逆定理证明出∠BAE=90°,然后在△ABD中运用勾股定理求出BD的长,从而得出BC=2BD.
【详解】解:延长AD到E,使DE=AD,连接BE.
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴AC=BE=13.
在△ABE中,AB=5,AE=12,BE=13,
∴AB2+AE2=BE2,
∴∠BAE=90°.
在△ABD中,∠BAD=90°,AB=5,AD=6,
∴BD=,
∴BC=.
故答案为:.
【点睛】本题考查了全等三角形的判定与性质,勾股定理及其逆定理,综合性较强,难度中等.题中延长中线的一倍是常用的辅助线的作法.
17.6
【分析】先利用勾股定理列式求出BC,再根据阴影部分面积等于以AC、BC为直径的两个半圆的面积加上直角三角形ABC的面积减去以AB为直径的半圆的面积,列式计算即可得解.
【详解】解:∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,
∵AB=5,AC=4,
∴,
S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC-直径为AB的半圆的面积
=
=
=
=
=
=6.
【点睛】本题考查了勾股定理,半圆的面积,熟记定理并观察图形表示出阴影部分的面积是解题的关键.
18.
【分析】根据勾股定理的逆定理可得,然后设,则,在中,根据勾股定理,即可求解.
【详解】解:∵,,,
∴,
∴,即,
设,则,
在中,,
∴,
解得:,
即.
故答案为:
【点睛】本题主要考查了勾股定理及其逆定理,根据题意得到是解题的关键.
19.(1)③,忽略了的情况;(2)见解析
【分析】(1)根据题意可直接进行求解;
(2)由因式分解及勾股定理逆定理可直接进行求解.
【详解】解:(1)由题意可得:从第③步开始错误,错的原因为:忽略了的情况;
故答案为③;忽略了的情况;
(2)正确的写法为:
当时,;当时,;
所以是直角三角形或等腰三角形或等腰直角三角形.
【点睛】本题主要考查勾股定理逆定理及因式分解,熟练掌握勾股定理逆定理及因式分解是解题的关键.
20.(1)CD长为12;(2)AB的长为25;(3)△ABC是直角三角形
【详解】解:在△BCD中,∵CD⊥AB,
∴BD2+CD2=BC2
∴CD2=BC2-BD2=152-92=144.
∴CD=12.
(2)在△ACD中,∵CD⊥AB,
∴CD2+AD2=AC2
∴AD2=AC2-CD2=202-122=256.
∴AD=16.
∴AB=AD+BD=16+9=25.
(3)∵BC2+AC2=152+202=625,AB2=252=625,
∴AB2=BC2+AC2
∴△ABC是直角三角形.
21.(1)24平方米;(2)4800元
【分析】(1)连接,在直角三角形中可求得的长,由、、的长度关系可得三角形为一直角三角形,为斜边;由此看,四边形的面积等于面积减的面积解答即可;
(2)根据题意列式计算即可.
【详解】解:(1)连接,
在中,,
在中,,,
而,
即,
,
.
(2)需费用(元),
答:总共需投入4800元.
【点睛】本题考查了勾股定理的应用,通过勾股定理由边与边的关系也可证明直角三角形,这样解题较为简单.
22.当点P运动的时间为7 s或25 s时,点P与顶点A的连线与腰垂直.
【分析】利用勾股定理求出AD的长,再利用勾股定理逆定理即可证明垂直.
【详解】(1)过点A作AD⊥BC于点D.
∵AB=AC,BC=8 cm,
∴BD=CD=BC=4 cm.
由勾股定理,得AD==3(cm).
分两种情况:(1)如图,当点P运动t秒后有PA⊥AC(P在线段BD上)时,
∵AP2=PD2+AD2=PC2-AC2,
∴PD2+32=(PD+4)2-52,∴PD=2.25 cm,
∴BP=4-2.25=1.75,
∴0.25t=1.75,解得t=7.
(2)当点P运动t秒后有PA⊥AB(P在线段CD上)时,同理可得PD=2.25,∴BP=4+2.25=6.25,
∴0.25t=6.25,解得t=25.
综上所述,当点P运动的时间为7 s或25 s时,点P与顶点A的连线与腰垂直.
【点睛】本题考查了勾股定理与勾股定理逆定理的应用,熟悉概念是解题关键.
23.(1)千米;
(2)平方千米
【分析】(1)根据勾股定理已知直角边求斜边计算;
(2)将四边形分成两个三角形,求证为直角,四边形面积为两个直角三角形面积之和.
【详解】(1)解:(1)∵∠B=90°,AB=BC=5千米,
∴(千米);
(2)∵(千米),(千米),(千米),
∴,,,
∴,
∴是直角三角形,则∠D=90°,
∴(平方千米).
【点睛】本题考查了勾股定理及其逆定理的应用,熟练掌握勾股定理的概念和公式并灵活运用是解题关键 .
24.(1)见解析
(2)海港C受台风影响,理由见解析
(3)3.5h
【分析】(1)根据勾股定理的逆定理,即可求解;
(2)过点C作于D.根据直角三角形的面积,可得,即可求解;
(3)在线段AB上取点E,F,使km,km,则台风中心在线段EF上时正好影响C港口.根据等腰三角形的性质可得ED=FD,然后根据勾股定理可得,从而得到km,即可求解.
【详解】(1)解:∵km,km,km,
∴.
∴是直角三角形,
∴;
(2)解:海港C受台风影响.理由如下:
如图,过点C作于D.
∵,
∴.
∵,
∴海港C受到台风影响.
(3)解:如图,在线段AB上取点E,F,使km,km,则台风中心在线段EF上时正好影响C港口.
∴EC=FC,
∵CD⊥AB,
∴ED=FD,
在中,由勾股定理得:
,
∴km,
∵台风的速度为40km/h,
∴.
∴台风影响该海港持续的时间为3.5h .
【点睛】本题主要考查了勾股定理的逆定理,勾股定理的实际应用,等腰三角形的性质,熟练掌握勾股定理的逆定理,正确构造直角三角形是解题的关键.
答案第1页,共2页
答案第1页,共2页
