2023-2024学年人教版数学八年级上册 12.2三角形全等的判定同步训练(无答案)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册 12.2三角形全等的判定同步训练(无答案) | 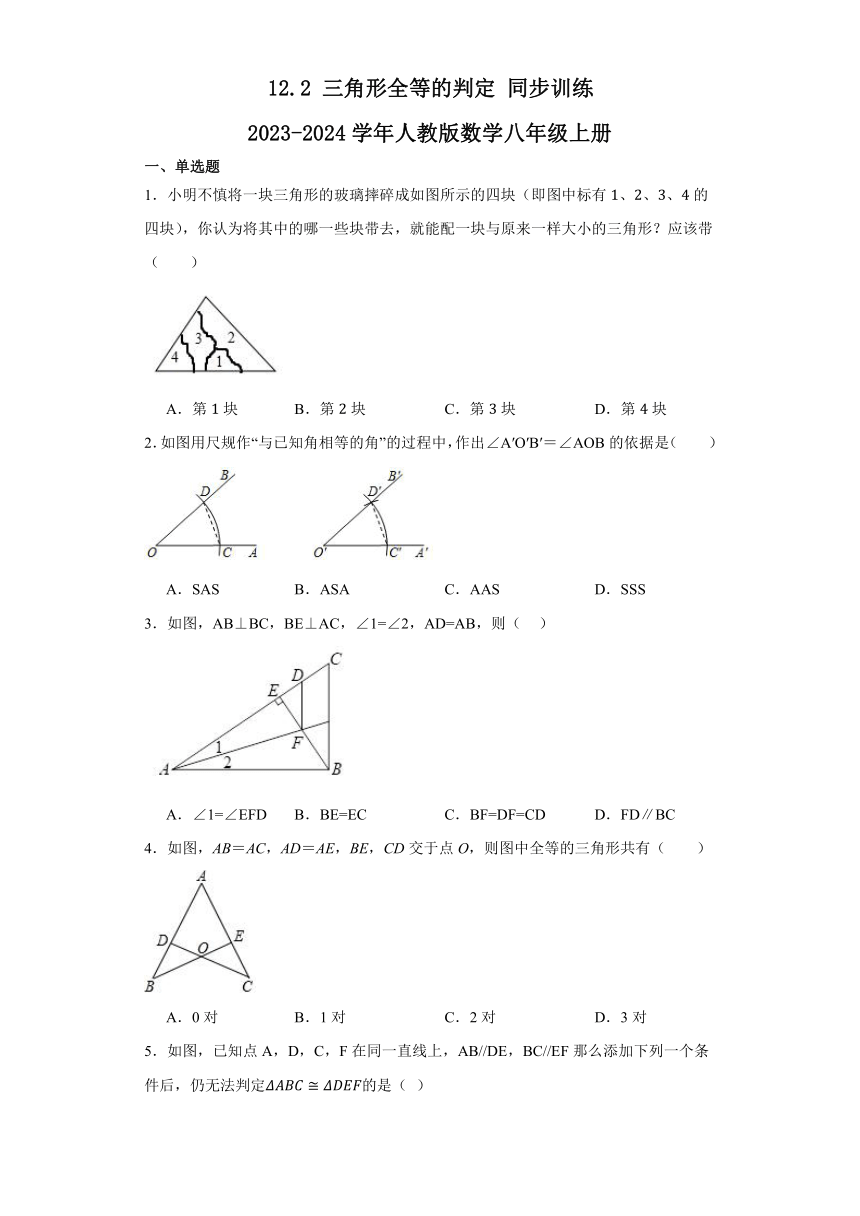 | |
| 格式 | docx | ||
| 文件大小 | 111.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 14:44:17 | ||
图片预览

文档简介
12.2 三角形全等的判定 同步训练
2023-2024学年人教版数学八年级上册
一、单选题
1.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有、、、的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形?应该带( )
A.第块 B.第块 C.第块 D.第块
2.如图用尺规作“与已知角相等的角”的过程中,作出∠A′O′B′=∠AOB的依据是( )
A.SAS B.ASA C.AAS D.SSS
3.如图,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )
A.∠1=∠EFD B.BE=EC C.BF=DF=CD D.FD∥BC
4.如图,AB=AC,AD=AE,BE,CD交于点O,则图中全等的三角形共有( )
A.0对 B.1对 C.2对 D.3对
5.如图,已知点A,D,C,F在同一直线上,AB//DE,BC//EF那么添加下列一个条件后,仍无法判定的是( )
A.AB=DE B.BC=EF C. D.AD=CF
6.如图,AC=BC,∠ACB=90°,AE平分∠BAC,BF⊥AE,交AC延长线于F,且垂足E,则以下结论:①AD=BF;②CD=CF;③AC+CD=AB;④AD=2BE.正确的个数是( )
A.个 B.个 C.个 D.个
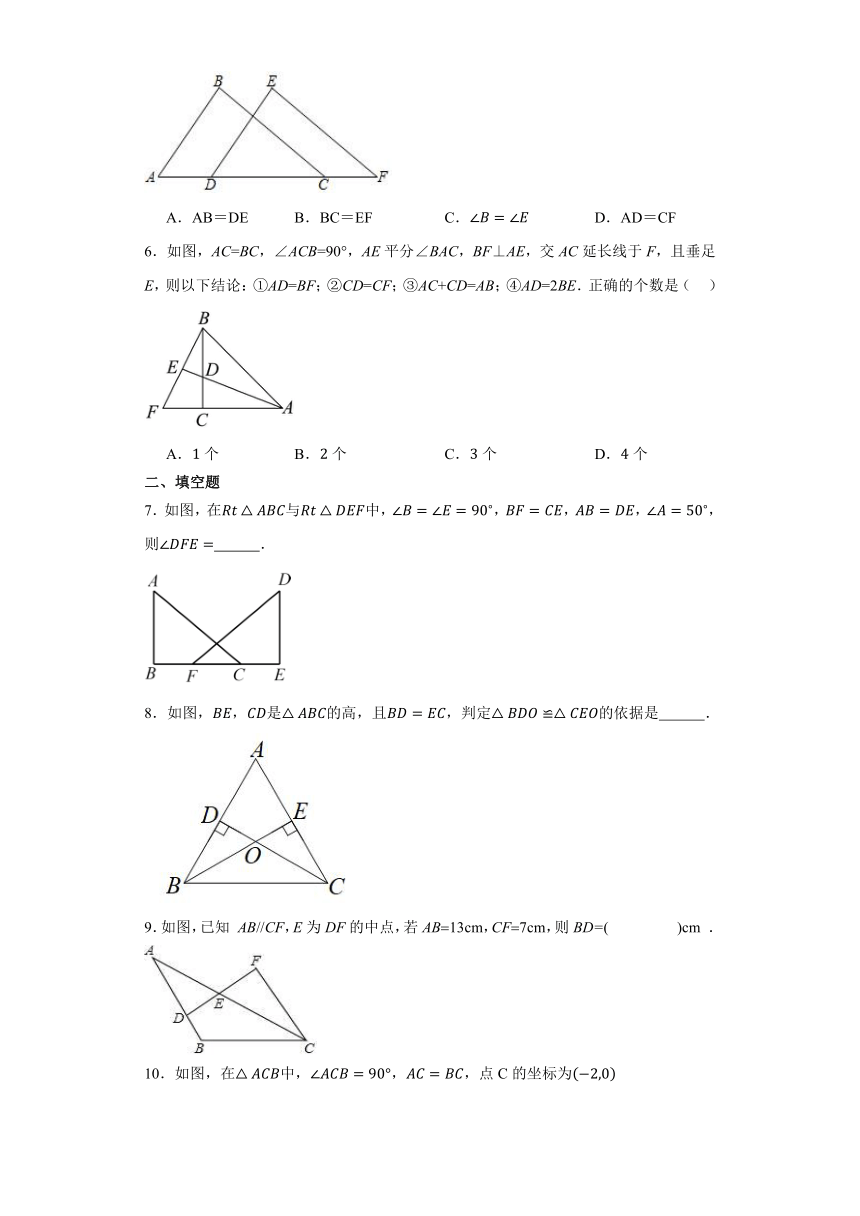
二、填空题
7.如图,在与中,,,,,则 .
8.如图,,是的高,且,判定的依据是 .
9.如图,已知 AB//CF,E为DF的中点,若AB13cm,CF7cm,则BD=( )cm .
10.如图,在中,,,点C的坐标为
,点A的坐标为,则B点的坐标是 .
11.如图,∠C=90°,AC=20,BC=10,AX⊥AC,点P和点Q同时从点A出发,分别在线段AC和射线AX上运动,且AB=PQ,当AP= 时,以点A,P,Q为顶点的三角形与△ABC全等.
三、解答题
12.AD⊥BD于D,BC⊥AC于C,BD=AC,求证:AD=BC.
13.如图,点、、在同一直线上,,,
求证:(1);
(2).
14.如图所示,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若AB=AC,DB=2,CE=5,求CF.
15.已知:如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°.
求证:(1)AC=BD;
(2)∠APB=50°.
2023-2024学年人教版数学八年级上册
一、单选题
1.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有、、、的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形?应该带( )
A.第块 B.第块 C.第块 D.第块
2.如图用尺规作“与已知角相等的角”的过程中,作出∠A′O′B′=∠AOB的依据是( )
A.SAS B.ASA C.AAS D.SSS
3.如图,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )
A.∠1=∠EFD B.BE=EC C.BF=DF=CD D.FD∥BC
4.如图,AB=AC,AD=AE,BE,CD交于点O,则图中全等的三角形共有( )
A.0对 B.1对 C.2对 D.3对
5.如图,已知点A,D,C,F在同一直线上,AB//DE,BC//EF那么添加下列一个条件后,仍无法判定的是( )
A.AB=DE B.BC=EF C. D.AD=CF
6.如图,AC=BC,∠ACB=90°,AE平分∠BAC,BF⊥AE,交AC延长线于F,且垂足E,则以下结论:①AD=BF;②CD=CF;③AC+CD=AB;④AD=2BE.正确的个数是( )
A.个 B.个 C.个 D.个
二、填空题
7.如图,在与中,,,,,则 .
8.如图,,是的高,且,判定的依据是 .
9.如图,已知 AB//CF,E为DF的中点,若AB13cm,CF7cm,则BD=( )cm .
10.如图,在中,,,点C的坐标为
,点A的坐标为,则B点的坐标是 .
11.如图,∠C=90°,AC=20,BC=10,AX⊥AC,点P和点Q同时从点A出发,分别在线段AC和射线AX上运动,且AB=PQ,当AP= 时,以点A,P,Q为顶点的三角形与△ABC全等.
三、解答题
12.AD⊥BD于D,BC⊥AC于C,BD=AC,求证:AD=BC.
13.如图,点、、在同一直线上,,,
求证:(1);
(2).
14.如图所示,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若AB=AC,DB=2,CE=5,求CF.
15.已知:如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°.
求证:(1)AC=BD;
(2)∠APB=50°.
