2.2 圆的对称性习题(无答案) 2023-2024学年苏科版数学九年级上册
文档属性
| 名称 | 2.2 圆的对称性习题(无答案) 2023-2024学年苏科版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 200.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 14:46:22 | ||
图片预览
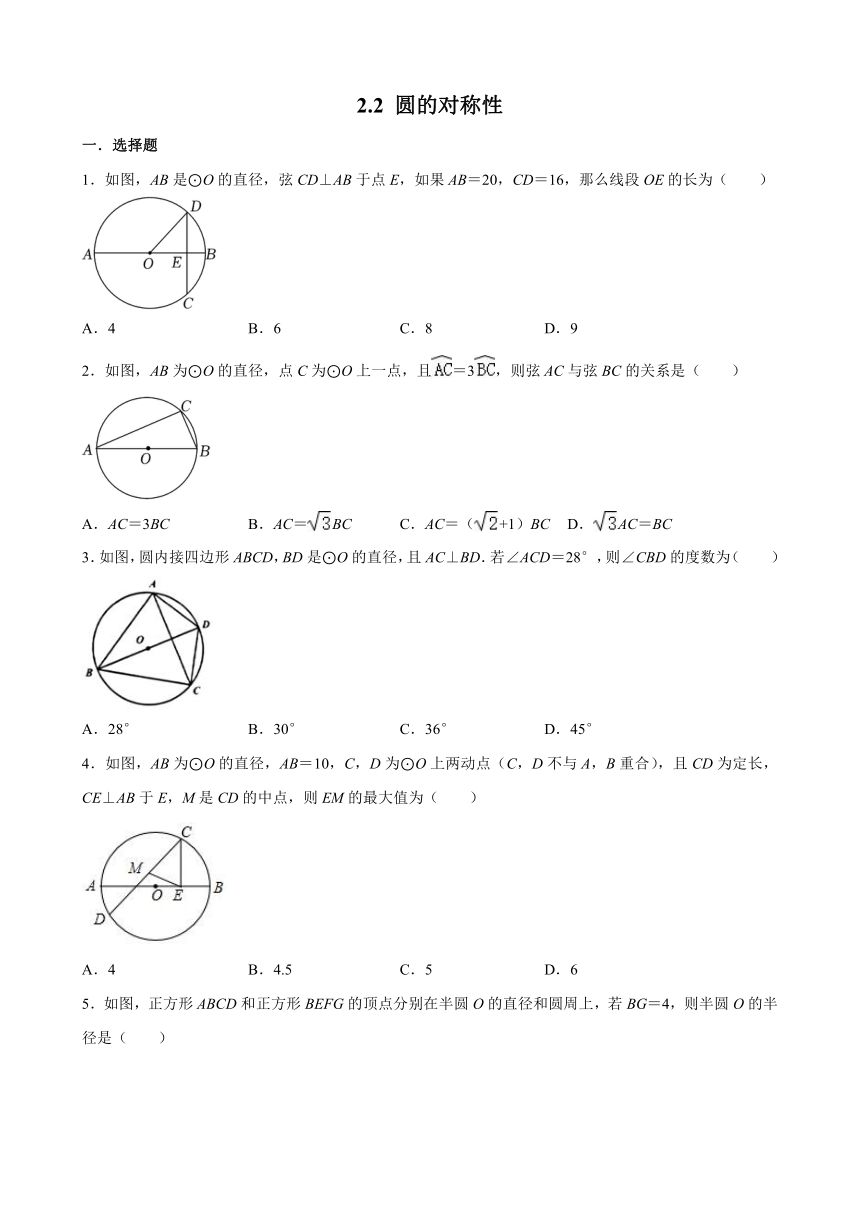
文档简介
2.2 圆的对称性
一.选择题
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果AB=20,CD=16,那么线段OE的长为( )
A.4 B.6 C.8 D.9
2.如图,AB为⊙O的直径,点C为⊙O上一点,且=3,则弦AC与弦BC的关系是( )
A.AC=3BC B.AC=BC C.AC=(+1)BC D.AC=BC
3.如图,圆内接四边形ABCD,BD是⊙O的直径,且AC⊥BD.若∠ACD=28°,则∠CBD的度数为( )
A.28° B.30° C.36° D.45°
4.如图,AB为⊙O的直径,AB=10,C,D为⊙O上两动点(C,D不与A,B重合),且CD为定长,CE⊥AB于E,M是CD的中点,则EM的最大值为( )
A.4 B.4.5 C.5 D.6
5.如图,正方形ABCD和正方形BEFG的顶点分别在半圆O的直径和圆周上,若BG=4,则半圆O的半径是( )
A.4+ B.9 C.4 D.6
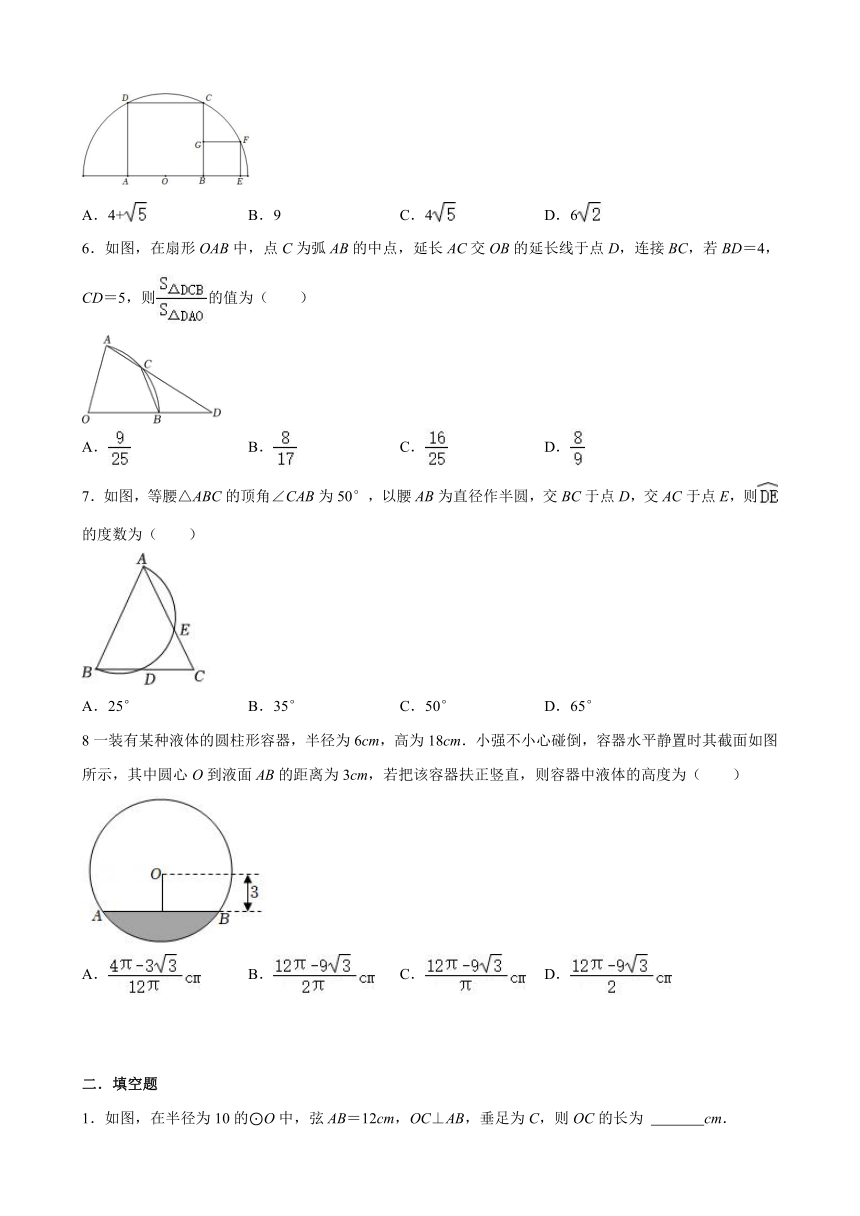
6.如图,在扇形OAB中,点C为弧AB的中点,延长AC交OB的延长线于点D,连接BC,若BD=4,CD=5,则的值为( )
A. B. C. D.
7.如图,等腰△ABC的顶角∠CAB为50°,以腰AB为直径作半圆,交BC于点D,交AC于点E,则的度数为( )
A.25° B.35° C.50° D.65°
8一装有某种液体的圆柱形容器,半径为6cm,高为18cm.小强不小心碰倒,容器水平静置时其截面如图所示,其中圆心O到液面AB的距离为3cm,若把该容器扶正竖直,则容器中液体的高度为( )
A. B. C. D.
二.填空题
1.如图,在半径为10的⊙O中,弦AB=12cm,OC⊥AB,垂足为C,则OC的长为 cm.
2.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8,OF=,则OE的长为
3.已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=
4.如图,AB是⊙O的直径,OD垂直于弦AC于点D,DO的延长线交⊙O于点E.若AC=4,DE=4,则BC的长是( )
5.《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其意思是:如图,AB为⊙O的直径,弦CD⊥AB于点E,BE=1寸,CD=1尺,那么直径AB的长为多少寸?(注:1尺=10寸)根据题意,该圆的直径为 寸.
三.解答题
1.如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,连接AC.
(1)求∠B的度数;
(2)若CE=4,求圆O的半径.
2.如图,在平行四边形ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
3.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,AD=CD.
(1)求证:OD∥BC;
(2)若AC=10,DE=4,求BC的长.
4.如图,点A、B、C在⊙O上,AB=CB=9,AD∥BC,CD⊥AD,且AD=2.
(1)求线段CD、AC的长;
(2)求⊙O的半径.
5.阅读以下材料,并按要求完成相应的任务关于圆的任务.
关于圆的引理
在《阿基米德全集》的《引理集》中,记述了古希腊的数学家、物理学家阿基米德提出的六个关于圆的引理,其中第二个引理为:如图,在半圆O中,P是上的任意一点,PN⊥直径AB于点N,D在直径AB上,且AN=ND,在上取一点Q,使,连接BQ,则BQ=BD.
任务:
(1)尺规作图:请根据材料,在图中补全图形.(保留作图痕迹,标明字母,不写作法).
(2)善思小组的同学尝试证明该引理,请按照下面的证明思路,写出该证明的剩余部分.
证明:连接PA,PD,PQ,QD.
……
一.选择题
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果AB=20,CD=16,那么线段OE的长为( )
A.4 B.6 C.8 D.9
2.如图,AB为⊙O的直径,点C为⊙O上一点,且=3,则弦AC与弦BC的关系是( )
A.AC=3BC B.AC=BC C.AC=(+1)BC D.AC=BC
3.如图,圆内接四边形ABCD,BD是⊙O的直径,且AC⊥BD.若∠ACD=28°,则∠CBD的度数为( )
A.28° B.30° C.36° D.45°
4.如图,AB为⊙O的直径,AB=10,C,D为⊙O上两动点(C,D不与A,B重合),且CD为定长,CE⊥AB于E,M是CD的中点,则EM的最大值为( )
A.4 B.4.5 C.5 D.6
5.如图,正方形ABCD和正方形BEFG的顶点分别在半圆O的直径和圆周上,若BG=4,则半圆O的半径是( )
A.4+ B.9 C.4 D.6
6.如图,在扇形OAB中,点C为弧AB的中点,延长AC交OB的延长线于点D,连接BC,若BD=4,CD=5,则的值为( )
A. B. C. D.
7.如图,等腰△ABC的顶角∠CAB为50°,以腰AB为直径作半圆,交BC于点D,交AC于点E,则的度数为( )
A.25° B.35° C.50° D.65°
8一装有某种液体的圆柱形容器,半径为6cm,高为18cm.小强不小心碰倒,容器水平静置时其截面如图所示,其中圆心O到液面AB的距离为3cm,若把该容器扶正竖直,则容器中液体的高度为( )
A. B. C. D.
二.填空题
1.如图,在半径为10的⊙O中,弦AB=12cm,OC⊥AB,垂足为C,则OC的长为 cm.
2.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8,OF=,则OE的长为
3.已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=
4.如图,AB是⊙O的直径,OD垂直于弦AC于点D,DO的延长线交⊙O于点E.若AC=4,DE=4,则BC的长是( )
5.《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其意思是:如图,AB为⊙O的直径,弦CD⊥AB于点E,BE=1寸,CD=1尺,那么直径AB的长为多少寸?(注:1尺=10寸)根据题意,该圆的直径为 寸.
三.解答题
1.如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,连接AC.
(1)求∠B的度数;
(2)若CE=4,求圆O的半径.
2.如图,在平行四边形ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
3.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,AD=CD.
(1)求证:OD∥BC;
(2)若AC=10,DE=4,求BC的长.
4.如图,点A、B、C在⊙O上,AB=CB=9,AD∥BC,CD⊥AD,且AD=2.
(1)求线段CD、AC的长;
(2)求⊙O的半径.
5.阅读以下材料,并按要求完成相应的任务关于圆的任务.
关于圆的引理
在《阿基米德全集》的《引理集》中,记述了古希腊的数学家、物理学家阿基米德提出的六个关于圆的引理,其中第二个引理为:如图,在半圆O中,P是上的任意一点,PN⊥直径AB于点N,D在直径AB上,且AN=ND,在上取一点Q,使,连接BQ,则BQ=BD.
任务:
(1)尺规作图:请根据材料,在图中补全图形.(保留作图痕迹,标明字母,不写作法).
(2)善思小组的同学尝试证明该引理,请按照下面的证明思路,写出该证明的剩余部分.
证明:连接PA,PD,PQ,QD.
……
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
