数学八年级上青岛版4.5方差课件4

课件25张PPT。4.5 方差（2）方差越大,说明数据的波动越大,越不稳定.方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).方差:各数据与它们的平均数的差的平方的平均数.复习回忆:
性质: (1)数据的方差都是非负数,即(2)当且仅当每个数据都相等时,方差为零,反过来,若 1．样本为101，98，102，100，99
的极差是 ， 方差是 . 2．甲、乙两个样本，甲样本方差是2.15，乙样本
方差是2.31，则甲样本和乙样本的离散程度（ ）
A．甲、乙离散程度一样
B．甲比乙的离散程度大
C．乙比甲的离散程度大
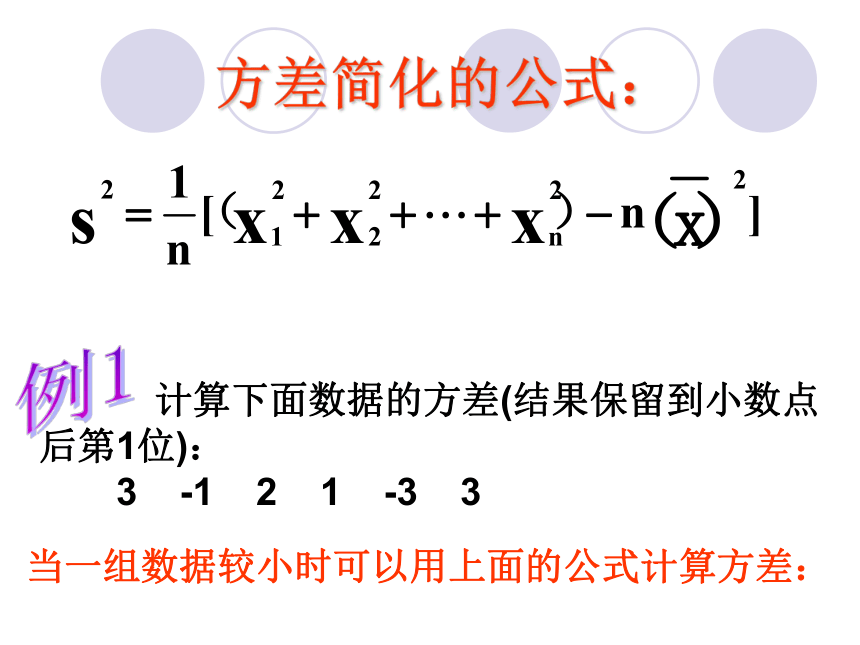
D．无法比较你会了吗?42C公式推导 以三个数为例方差还有简便公式吗？：方差的简便公式： 方差简化的公式：　　　计算下面数据的方差(结果保留到小数点后第1位)：
　　3 -1 2 1 -3 3例1当一组数据较小时可以用上面的公式计算方差：方差:各数据与它们的平均数的差的平方的平均数. 当一组数据较大时，
可按基本公式计算方差：
数据的单位与方差的单位一致吗？怎样解决?动动脑！为了使单位一致，可用方差的算术平方根：来表示，并把它叫做标准差（standardeviation）.方差=标准差的平方 标准差=方差的算术平方根
S=1、在统计中，样本的方差和标准差可以近似的反映总体的（　　）．
Ａ、平均状态
Ｂ、离散程度
Ｃ、分布规律
Ｄ、最大值和最小值牛刀小试Ｂ2、刘翔为了备战2008年奥运会，刻苦进行110米跨栏训练，为判断他的成绩是否稳定，教练对他10次训练的成绩进行统计分析，则教练需了解刘翔这10次成绩的（ ）
A、众数 B、方差
C、平均数 D、频数牛刀小试Ｂ1、在方差的计算公式 S2= [（x1－20)2+(x2－20)2+ +(x10－20)2]中,数字10和20分别表示( )
A、样本的容量和方差 B、平均数和样本的容量
C、样本的容量和平均数 D、样本的方差和平均数C牛刀小试3、对于数据3、2、1、0、-1
求：它的极差是————
方差是—————
标准差是————— 牛刀小试 说说你是怎样思考，并口述求解过程？42(1)有5个数1，4，a, 5, 2的平均数是a，则这个
5个数的方差是_____.
(2)绝对值小于 所有整数的标准差是______.
(3)一组数据：a, a, a, ---,a (有n个a)则它的方差和标准差为___　　　;20牛刀小试0农科院对甲,乙两种甜玉米各用10块试验田进行
试验,得到两个品种每公顷产量的两种数据:根据这些数据，应为农科院选择甜玉米种子提出怎样的建议？说明在试验田中,甲,乙两种甜玉米的平均产量相差不大,由此估计在这个地区种植这两种甜玉米,它们的平均产量相差不大.用计算器算得样本数据的方差是：
S2甲≈0.01,　S2乙≈0.002 得出 S2甲＞S2乙
说明在试验田中,乙种甜玉米的产量比较稳定,进而可以推测要这个地区种植乙种甜玉米的产量比甲的稳定. 综合考虑甲乙两个品种的产量和产量的稳定性,可以推测这个地区更适合种植乙种甜玉米.解：例：一次科技知识竞赛,两组学生成绩统计如下:已经算得两个组的人平均分都是80分,请根据你所
学过的统计知识,进一步判断这两个组在这次竞赛
中的成绩谁优谁劣,并说明理由.解: (1)甲组成绩的众数为90分,乙组成绩的众数为70分, 以成绩的众数比较看,甲组成绩好些.(3)甲、乙两组成绩的中位数都是80分,甲组成绩在中位数以上(包括中位数)的人有33人,乙组成绩在中位数以上(包括中位数)的人有26人,从这一角度,看甲组成绩总体较好;
(4)从成绩统计表看,甲组成绩高于80分的人数为20人,乙组成绩高于80分的人数为24人,乙组成绩集中在高分段的人数多,同时,乙组得满分的人数比甲组得满分的人数多6人,从这一角度看,乙组的成绩较好.
3.某农民几年前承包了甲、乙两片荒山，各栽了100棵
蜜橘，成活98%，现已挂果，经济效益显著，为了
分析经营情况，他从甲山随意采摘了3棵树上的蜜橘
称得质量分别为25，18，20千克；他从乙山随意采摘
了4棵树上的蜜橘，称得质量分别为21，24，19、20
千克。组成一个样本，问：
（1）样本容量是多少？
（2）样本平均数是多少？并估算出甲、乙两山蜜橘
的总产量？
（3）甲、乙两山哪个山上蜜橘长势较整齐？（3+4=7）（2）探索发现已知三组数据1、2、3、4、5；11、12、13、14、15
和3、6、9、12、15。1、求这三组数据的平均数、方差和标准差。2、对照以上结果，你能从中发现哪些有趣的结论？
想看一看下面的问题吗？32132918请你用发现的结论来解决以下的问题：
已知数据a1，a2，a3，…，an的平均数为X，方差为Y, 则
①数据a1+3，a2 + 3，a3 +3 ，…，an +3的平均数为--------，方差为-------

②数据a1-3，a2 -3，a3 -3 ，…，an -3的平均数为 ----------，方差为--------

③数据3a1，3a2 ，3a3 ，…，3an的平均数为-----------，方差为----------.

④数据2a1-3，2a2 -3，2a3 -3 ，…，2an -3的平均数为 ----------，
方差为---------. X+3YX-3Y3X9Y2X-34Y平均数、方差、标准差的几个规律一、方差和标准差的计算公式小结二、方差的简化计算公式（数小时）（数大时）数理统计的基本思想：
用样本估计总体.
用样本的某些特性估计总体相应的特性.
用样本的平均数、中位数和众数去估计相应总体的平均水平特性.
用样本的方差去估计相应总体数据的波动情况.作业:《数学课本》
P144-145
P153-154欢迎指导