数学八年级上青岛版5.5三角形内角和定理课件7
文档属性
| 名称 | 数学八年级上青岛版5.5三角形内角和定理课件7 |

|
|
| 格式 | zip | ||
| 文件大小 | 365.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-28 00:00:00 | ||
图片预览




文档简介
课件22张PPT。青岛版 八年级数学(上 )5.5 三角形内角和定理(2)回忆之前学过哪些与180°有关的结论? (1)平行线有什么性质? 课前准备(3)命题“三角形三个内角的和是180 °”的
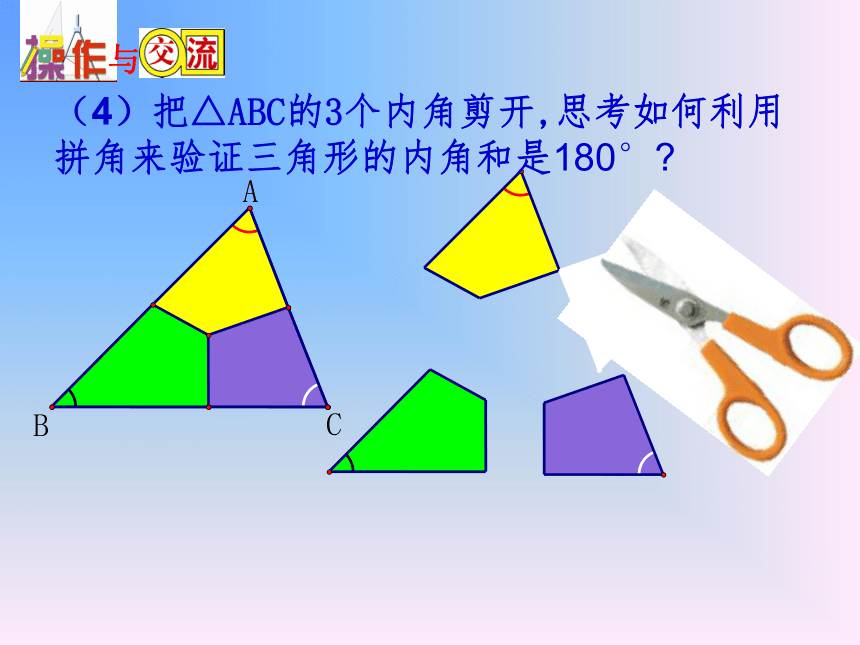
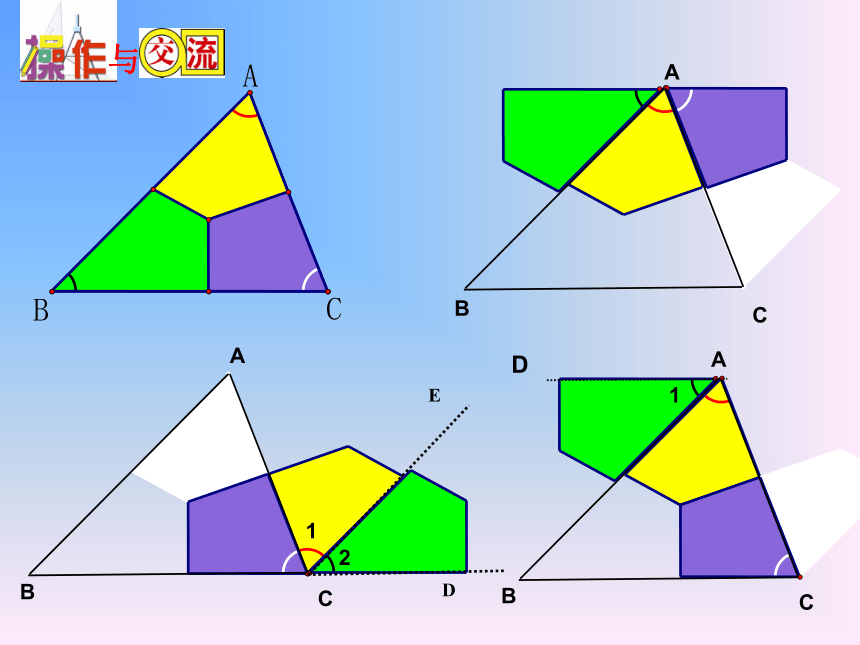
题设和结论分别是什么?知识回顾想一想把三个角拼在一起试试看有什么办法可以验证呢?
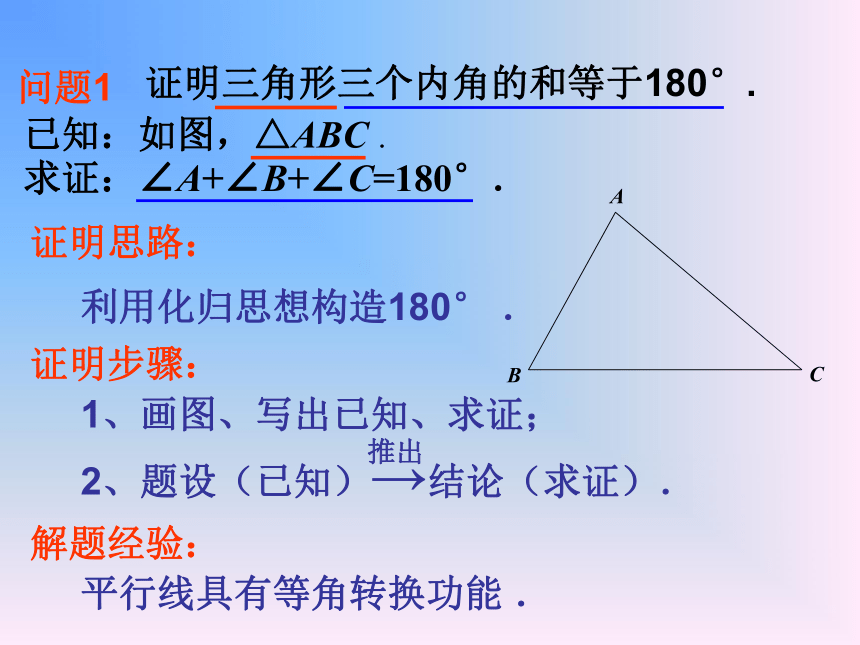
(4)把△ABC的3个内角剪开,思考如何利用拼角来验证三角形的内角和是180°?与与问题1已知:如图,△ABC .证明三角形三个内角的和等于180°.求证:∠A+∠B+∠C=180°. 证明思路:利用化归思想构造180° .证明步骤:1、画图、写出已知、求证;2、题设(已知)→结论(求证).推出解题经验:平行线具有等角转换功能 .证明:∴∠___=∠___, ∠___=∠___ ∵∠___+∠______+∠____=180° ∴∠____+∠______+∠____=180°已知:△ABC.
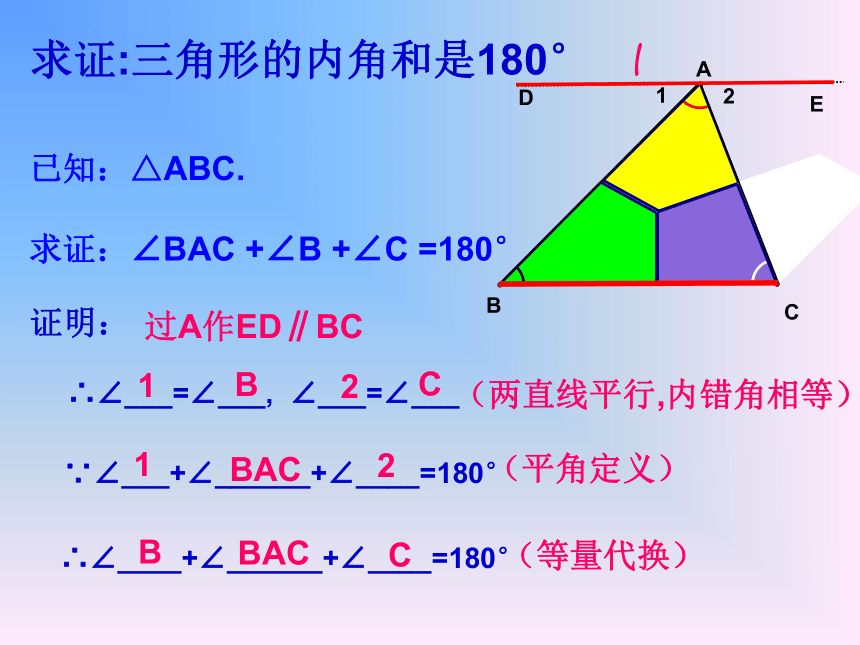
求证:∠BAC +∠B +∠C =180°l求证:三角形的内角和是180°过A作ED∥BC
(平角定义)
(等量代换)
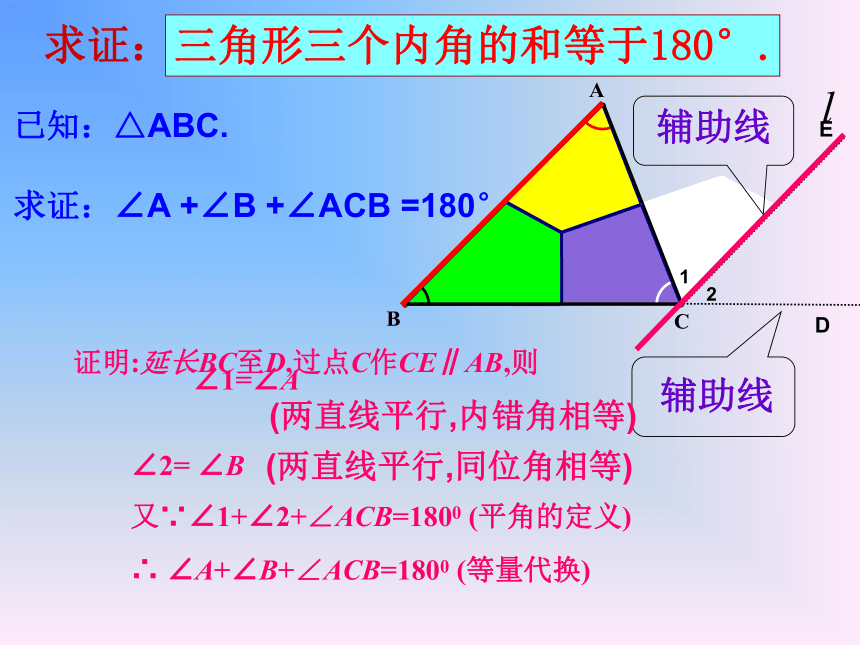
(两直线平行,内错角相等)11BACC2C2BBBAC12DE证明:延长BC至D,过点C作CE∥AB,则 ∠1=∠A ∠2= ∠B 又∵∠1+∠2+∠ACB=1800 (平角的定义) ∴ ∠A+∠B+∠ACB=1800 (等量代换)已知:△ABC.
求证:∠A +∠B +∠ACB =180°辅助线(两直线平行,内错角相等)(两直线平行,同位角相等)与121ABCDE1、为了证明三个角的和为180°,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法. 2、为了证明的需要,在原来的图形上自己加上的
线叫做辅助线。在平面几何里,辅助线通常画成虚线。
注意要说明所加辅助线的位置、名称和所满足的条件。 3、在本题的证明中,添加平行线的作用之一是移动角。D思路总结: 在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。思路总结 为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.三角形内角和定理:
三角形的内角和等于1800.1、填空
(1) 在△ABC中,∠A=30°∠B=500, 则∠C=____。
(2) 在△ABC中,∠C=90°∠B=500, 则∠A=____。
(3)在△ABC中, ∠A=400,∠A=2∠B,则∠C=____。
(4)在△ABC中, ∠A等于直角的一半,∠B等于直角的 ,则∠C=__。活动1:比一比,赛一赛你真行!看哪一组做得又对又快!2、如图,在△ABC中, ∠ABC=70°, ∠C=65°,BD⊥AC于D, 求∠ABD, ∠CBD的度数。活动2:学会应用 例1:在△ABC中,∠A :∠ B: ∠ C= 1: 2: 3,求∠ ABC的度数。 解: ∵ ∠ A :∠ B: ∠ C= 1: 2: 3,
∴ ∠ B=2 ∠ A, ∠ C=3 ∠ A
又∠ A +∠ B+ ∠ C=1800
∴ ∠ A+2 ∠ A+3 ∠ A=1800
∴ ∠ A=300, ∠ B=600, ∠ C=900。做一做4、直角三角形的两锐角之和是_____度;90结论:直角三角形的两个锐角互余。5、如右图,在△ABC中
∠ACB=90°, CD⊥AB,
∠B=50°.则∠DCA=___ 40 °?例:如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°.从C处观测A、B两处时视角∠ACB是多少?30°45°综合运用1、如图,在△ABC中,DE∥BC,∠A=60°,
∠C=70°,则 ∠ADE=__________
做一做题组二:50°2、如图,C岛在A岛的北偏东50°方
向,B岛在A岛的北偏东80°方向,C
岛在B岛的北偏西40°方向,
(1)∠DAC=_________,∠DAB=_________
∠CBE=__________,∠CAB=_________
(2)从C岛看A、B两岛的视角∠ACB是多少度?
做一做50°80°40°30°B 你能想出一个更简捷的方法来求∠C的度数吗?1250°40°解: 过点C画CF∥AD
∴ ∠1=∠DAC=50 °F∵ CF∥AD, 又AD ∥BE∴ CF∥ BE∴∠2=∠CBE =40 °∴ ∠ACB=∠1﹢∠2 =50 °﹢ 40 ° =90 °(两直线平行,内错角相等)(平行于同一直线的两直线互相平行)(两直线平行,内错角相等)3、一块模板如图所示,按规定AF、DE
的延长线相交成85°角,因交点不在板
上,不便测量,工人师傅连结AD,测得
∠FAD=34°,∠ADE=63°,那么这块
模板符合不符合规定?为什么?
M34 °63 °(1)一个三角形中最多有 个直角
(2)一个三角形中最多有 个钝角
(3)一个三角形中至少有 个锐角
(4)任意一个三角形中,最大的一个角的
度数至少为 .60°211思考回顾与小结1、三角形内角和的定理:三角形三个内角的和等于180 °.
4、三角形内角和的定理证明中,添加平行线的目的是移动角.
2、证明三角形内角和定理中运用了转化思想;
3、解题过程中,可以根据需要添加辅助线;练一练
已知:如图在△ABC中,AD垂直BC,点D为 垂足, ∠ BAD=∠C
求证: △ABC为直角三角形
ABCD
题设和结论分别是什么?知识回顾想一想把三个角拼在一起试试看有什么办法可以验证呢?
(4)把△ABC的3个内角剪开,思考如何利用拼角来验证三角形的内角和是180°?与与问题1已知:如图,△ABC .证明三角形三个内角的和等于180°.求证:∠A+∠B+∠C=180°. 证明思路:利用化归思想构造180° .证明步骤:1、画图、写出已知、求证;2、题设(已知)→结论(求证).推出解题经验:平行线具有等角转换功能 .证明:∴∠___=∠___, ∠___=∠___ ∵∠___+∠______+∠____=180° ∴∠____+∠______+∠____=180°已知:△ABC.
求证:∠BAC +∠B +∠C =180°l求证:三角形的内角和是180°过A作ED∥BC
(平角定义)
(等量代换)
(两直线平行,内错角相等)11BACC2C2BBBAC12DE证明:延长BC至D,过点C作CE∥AB,则 ∠1=∠A ∠2= ∠B 又∵∠1+∠2+∠ACB=1800 (平角的定义) ∴ ∠A+∠B+∠ACB=1800 (等量代换)已知:△ABC.
求证:∠A +∠B +∠ACB =180°辅助线(两直线平行,内错角相等)(两直线平行,同位角相等)与121ABCDE1、为了证明三个角的和为180°,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法. 2、为了证明的需要,在原来的图形上自己加上的
线叫做辅助线。在平面几何里,辅助线通常画成虚线。
注意要说明所加辅助线的位置、名称和所满足的条件。 3、在本题的证明中,添加平行线的作用之一是移动角。D思路总结: 在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。思路总结 为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.三角形内角和定理:
三角形的内角和等于1800.1、填空
(1) 在△ABC中,∠A=30°∠B=500, 则∠C=____。
(2) 在△ABC中,∠C=90°∠B=500, 则∠A=____。
(3)在△ABC中, ∠A=400,∠A=2∠B,则∠C=____。
(4)在△ABC中, ∠A等于直角的一半,∠B等于直角的 ,则∠C=__。活动1:比一比,赛一赛你真行!看哪一组做得又对又快!2、如图,在△ABC中, ∠ABC=70°, ∠C=65°,BD⊥AC于D, 求∠ABD, ∠CBD的度数。活动2:学会应用 例1:在△ABC中,∠A :∠ B: ∠ C= 1: 2: 3,求∠ ABC的度数。 解: ∵ ∠ A :∠ B: ∠ C= 1: 2: 3,
∴ ∠ B=2 ∠ A, ∠ C=3 ∠ A
又∠ A +∠ B+ ∠ C=1800
∴ ∠ A+2 ∠ A+3 ∠ A=1800
∴ ∠ A=300, ∠ B=600, ∠ C=900。做一做4、直角三角形的两锐角之和是_____度;90结论:直角三角形的两个锐角互余。5、如右图,在△ABC中
∠ACB=90°, CD⊥AB,
∠B=50°.则∠DCA=___ 40 °?例:如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°.从C处观测A、B两处时视角∠ACB是多少?30°45°综合运用1、如图,在△ABC中,DE∥BC,∠A=60°,
∠C=70°,则 ∠ADE=__________
做一做题组二:50°2、如图,C岛在A岛的北偏东50°方
向,B岛在A岛的北偏东80°方向,C
岛在B岛的北偏西40°方向,
(1)∠DAC=_________,∠DAB=_________
∠CBE=__________,∠CAB=_________
(2)从C岛看A、B两岛的视角∠ACB是多少度?
做一做50°80°40°30°B 你能想出一个更简捷的方法来求∠C的度数吗?1250°40°解: 过点C画CF∥AD
∴ ∠1=∠DAC=50 °F∵ CF∥AD, 又AD ∥BE∴ CF∥ BE∴∠2=∠CBE =40 °∴ ∠ACB=∠1﹢∠2 =50 °﹢ 40 ° =90 °(两直线平行,内错角相等)(平行于同一直线的两直线互相平行)(两直线平行,内错角相等)3、一块模板如图所示,按规定AF、DE
的延长线相交成85°角,因交点不在板
上,不便测量,工人师傅连结AD,测得
∠FAD=34°,∠ADE=63°,那么这块
模板符合不符合规定?为什么?
M34 °63 °(1)一个三角形中最多有 个直角
(2)一个三角形中最多有 个钝角
(3)一个三角形中至少有 个锐角
(4)任意一个三角形中,最大的一个角的
度数至少为 .60°211思考回顾与小结1、三角形内角和的定理:三角形三个内角的和等于180 °.
4、三角形内角和的定理证明中,添加平行线的目的是移动角.
2、证明三角形内角和定理中运用了转化思想;
3、解题过程中,可以根据需要添加辅助线;练一练
已知:如图在△ABC中,AD垂直BC,点D为 垂足, ∠ BAD=∠C
求证: △ABC为直角三角形
ABCD
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
