数学八年级下青岛版6.4 三角形的中位线定理课件8
文档属性
| 名称 | 数学八年级下青岛版6.4 三角形的中位线定理课件8 |

|
|
| 格式 | zip | ||
| 文件大小 | 139.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-28 00:00:00 | ||
图片预览






文档简介
课件16张PPT。三角形的中位线把任意一个三角形分成四个全等的三角形.
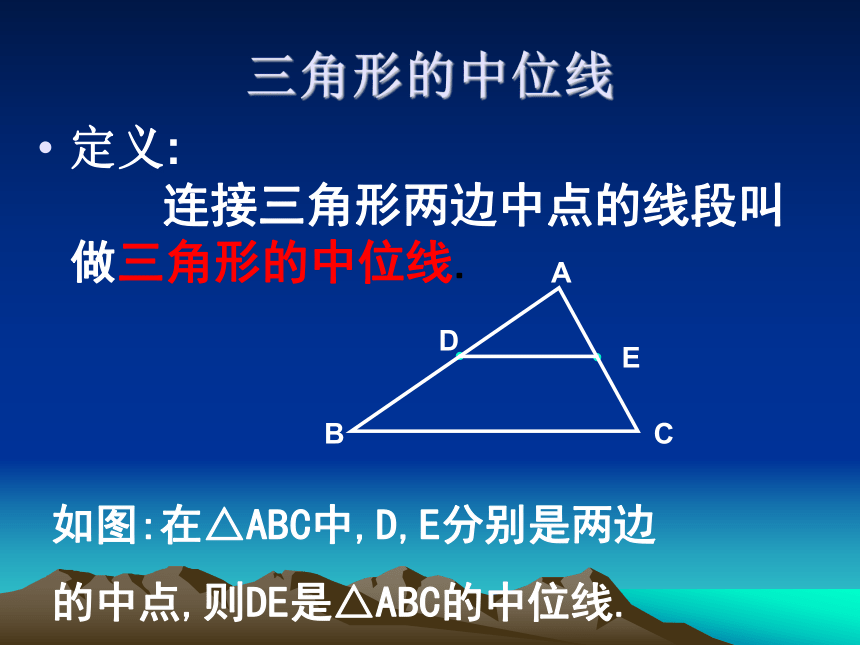
做法:连接每两边的中点.做一做你认为这种做法对吗?三角形的中位线定义: 连接三角形两边中点的线段叫做三角形的中位线.如图:在△ABC中,D,E分别是两边
的中点,则DE是△ABC的中位线.你能猜出三角形的中位线与第三边
有怎样的关系?如图:在△ABC中,D,E分别是两边
的中点,则DE是△ABC的中位线. 三角形的中位线平行于第三边,
并且等于它的一半。你能证明吗?三角形中位线定理:
三角形的中位线平行于第三边,并且等于它的一半。
已知:在△ABC中,AE=EB,AF=FC。
求证:EF∥BC,EF= BC
证明: 延长线段EF到M,使FM=EF,连结MC
∵ AF=FC ∠AFE= ∠CFM EF=FM
∴ △AFE≌△CFM (SAS)
∴ ∠AEF= ∠M ∠A= ∠FCM
∴ AB∥CM EF∥BC
∴ 四边形EBCM是平行四边形
∴ EM=BC
∵EF= EM
∴EF= BC
1、如图:EF是△ABC 的中位线,BC=20,则EF= ( ) ;
抢 答 题10 2、在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,则EF和MN的关系是( )抢 答 题平行且相等3、已知:三角形的各边分别为6cm、8cm 和10cm,则连结各边中点所成的三角形的周长是( )
抢 答 题12cm 求证:顺次连结四边形四条边的中点所得的四边形是平行四边形。
例 题 已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形. 求证:顺次连结四边形四条边的中点所得的四边形是平行四边形。
例 题 已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连结AC.
∵AH=HD,CG=GD
∴HG∥AC, HG= AC
同理 EF∥AC EF= AC
∴HG∥EF HG=EF
∴四边形EFGH是平行四边形.
巩固练习 答:A、B两点的距离是40m。因为MN是△ABC的中位线,利用三角形中位线定理得MN等于AB的一半,所以AB为MN的2倍,等于40m.⑴ A、B两点被池塘隔开,在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN = 20m,那么A、B两点的距离是多少?为什么?下⑵已知:三角形的各边分别为6cm,8cm, 10cm,则连结各边中点所成三角形的周长为——cm,面积为——cm2,为原三角形面积的——。下(3)如图,AF=FD=DB,FG∥DE∥BC,PE=1.5,则DP= ———,BC= ———34.59下BC=CD,则顺次连结它的各边中点得到的四边形是( )A 等腰梯形C 菱形D 正方形B 矩形(4)在四边形ABCD中,AB=AD,总结连接三角形两边中点的线段叫做三角形的中位线.
三角形中位线性质:三角形的中位线平行于三角形中位线定义:连接三角形两边中点第三边,且等于第三边的一半.家庭作业P85习题3.3
第3、4
做法:连接每两边的中点.做一做你认为这种做法对吗?三角形的中位线定义: 连接三角形两边中点的线段叫做三角形的中位线.如图:在△ABC中,D,E分别是两边
的中点,则DE是△ABC的中位线.你能猜出三角形的中位线与第三边
有怎样的关系?如图:在△ABC中,D,E分别是两边
的中点,则DE是△ABC的中位线. 三角形的中位线平行于第三边,
并且等于它的一半。你能证明吗?三角形中位线定理:
三角形的中位线平行于第三边,并且等于它的一半。
已知:在△ABC中,AE=EB,AF=FC。
求证:EF∥BC,EF= BC
证明: 延长线段EF到M,使FM=EF,连结MC
∵ AF=FC ∠AFE= ∠CFM EF=FM
∴ △AFE≌△CFM (SAS)
∴ ∠AEF= ∠M ∠A= ∠FCM
∴ AB∥CM EF∥BC
∴ 四边形EBCM是平行四边形
∴ EM=BC
∵EF= EM
∴EF= BC
1、如图:EF是△ABC 的中位线,BC=20,则EF= ( ) ;
抢 答 题10 2、在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,则EF和MN的关系是( )抢 答 题平行且相等3、已知:三角形的各边分别为6cm、8cm 和10cm,则连结各边中点所成的三角形的周长是( )
抢 答 题12cm 求证:顺次连结四边形四条边的中点所得的四边形是平行四边形。
例 题 已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形. 求证:顺次连结四边形四条边的中点所得的四边形是平行四边形。
例 题 已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连结AC.
∵AH=HD,CG=GD
∴HG∥AC, HG= AC
同理 EF∥AC EF= AC
∴HG∥EF HG=EF
∴四边形EFGH是平行四边形.
巩固练习 答:A、B两点的距离是40m。因为MN是△ABC的中位线,利用三角形中位线定理得MN等于AB的一半,所以AB为MN的2倍,等于40m.⑴ A、B两点被池塘隔开,在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN = 20m,那么A、B两点的距离是多少?为什么?下⑵已知:三角形的各边分别为6cm,8cm, 10cm,则连结各边中点所成三角形的周长为——cm,面积为——cm2,为原三角形面积的——。下(3)如图,AF=FD=DB,FG∥DE∥BC,PE=1.5,则DP= ———,BC= ———34.59下BC=CD,则顺次连结它的各边中点得到的四边形是( )A 等腰梯形C 菱形D 正方形B 矩形(4)在四边形ABCD中,AB=AD,总结连接三角形两边中点的线段叫做三角形的中位线.
三角形中位线性质:三角形的中位线平行于三角形中位线定义:连接三角形两边中点第三边,且等于第三边的一半.家庭作业P85习题3.3
第3、4
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
