数学八年级下青岛版11.1图形的平移课件3
文档属性
| 名称 | 数学八年级下青岛版11.1图形的平移课件3 |

|
|
| 格式 | zip | ||
| 文件大小 | 859.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-28 00:00:00 | ||
图片预览



文档简介
课件27张PPT。第十一章:图形的平移与旋转§11.1图形的平移(3) 在平面内,将一个图形沿某一个方向移动
一定的距离,图形的这种变化叫做平移。
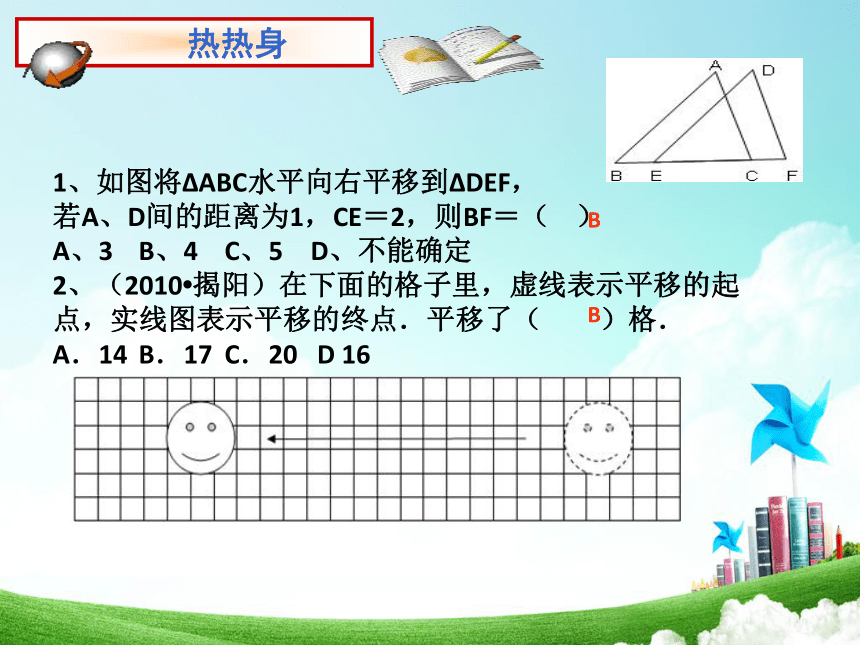
平移只改变图形的 不改变图形的 。位置形状和大小平移定义:平移性质 一个图形和它经过平移所得的图形中,一个图形和它平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等;1、如图将ΔABC水平向右平移到ΔDEF,
若A、D间的距离为1,CE=2,则BF=( )
A、3 B、4 C、5 D、不能确定
2、(2010?揭阳)在下面的格子里,虚线表示平移的起点,实线图表示平移的终点.平移了( )格.
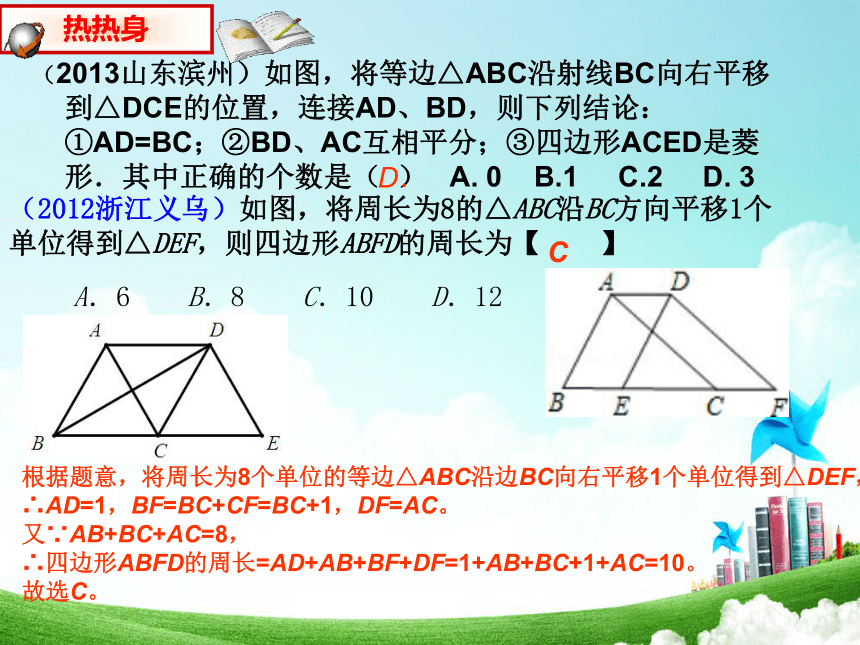
A.14 B.17 C.20 D 16BB(2013山东滨州)如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是( ) A. 0 B.1 C.2 D. 3D. (2012浙江义乌)如图,将周长为8的△ABC沿BC方向平移1个
单位得到△DEF,则四边形ABFD的周长为【 】 A.6 B.8 C.10 D.12C 根据题意,将周长为8个单位的等边△ABC沿边BC向右平移1个单位得到△DEF,
∴AD=1,BF=BC+CF=BC+1,DF=AC。
又∵AB+BC+AC=8,
∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10。
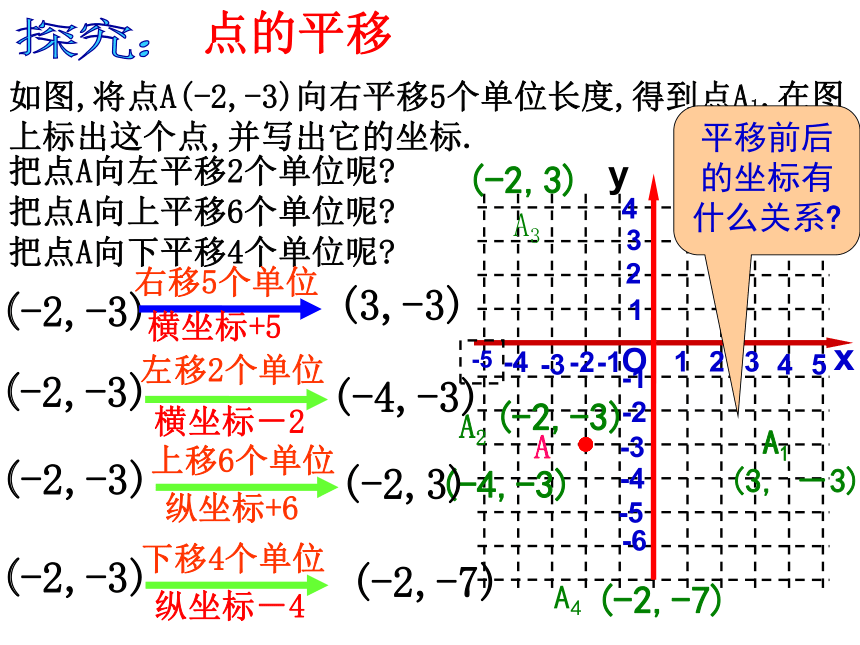
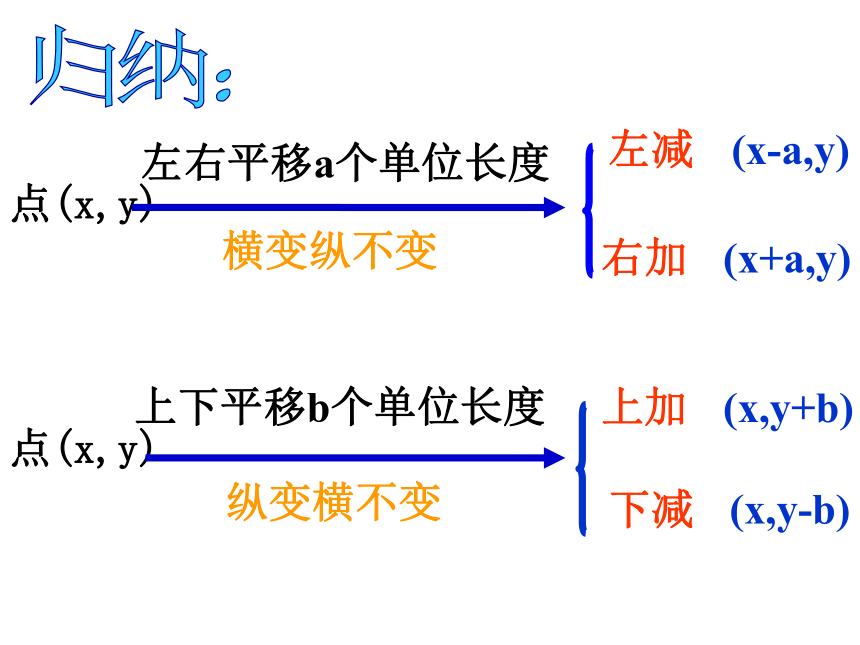
故选C。如图,将点A(-2,-3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.把点A向左平移2个单位呢?xyO12342413-1-2-3-4-5-1-2-3-4-55-6A1(3, -3)A(-2,-3)把点A向上平移6个单位呢?A2(-4,-3)把点A向下平移4个单位呢?A3(-2,3)A4(-2,-7)(-2,-3)右移5个单位(3,-3)横坐标+5(-2,-3)左移2个单位(-4,-3)横坐标-2(-2,-3)上移6个单位(-2,3)纵坐标+6(-2,-3)下移4个单位(-2,-7)纵坐标-4探究:平移前后的坐标有什么关系?点的平移归纳:点(x,y)左右平移a个单位长度(x-a,y)点(x,y)上下平移b个单位长度纵变横不变横变纵不变左减(x+a,y)右加(x,y+b)上加(x,y-b)下减向右平移
a个单位向左平移
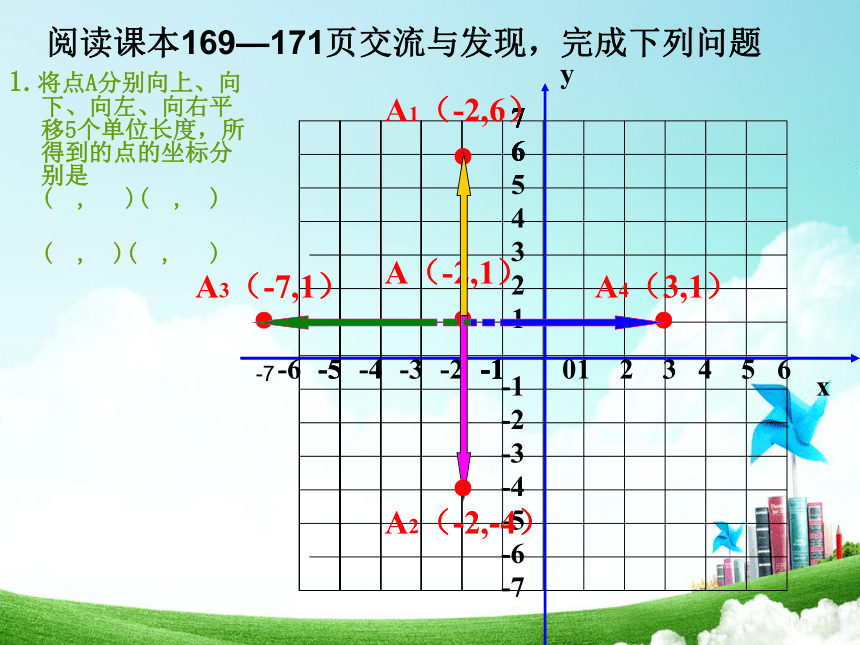
a个单位归纳P(x, y)P(x-a, y)P(x+a, y)P(x, y+b)P(x, y-b)左减右加上加下减1.将点A分别向上、向下、向左、向右平移5个单位长度,所得到的点的坐标分别是( , )( , )
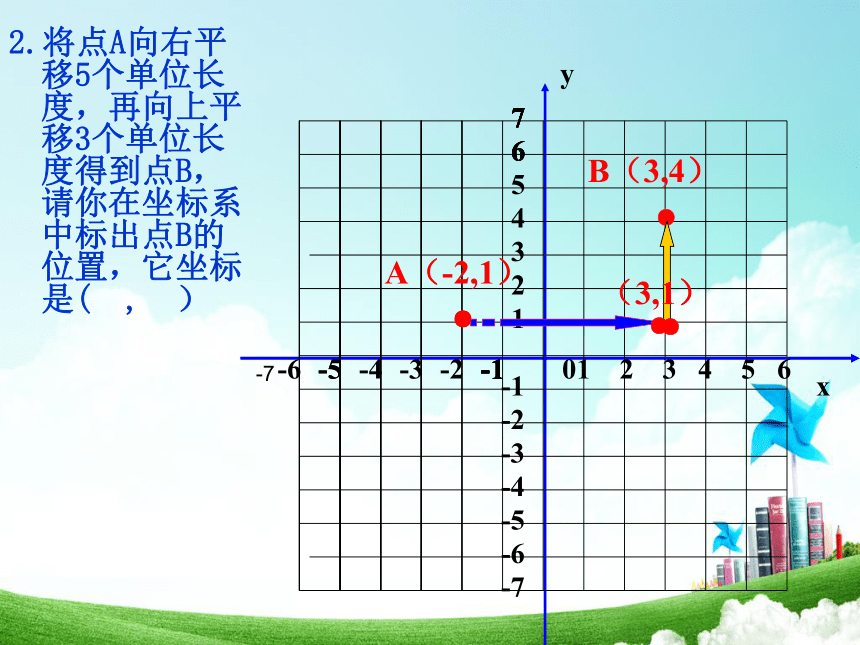
( , )( , ) 阅读课本169—171页交流与发现,完成下列问题●A(-2,1)-72.将点A向右平移5个单位长度,再向上平移3个单位长度得到点B,请你在坐标系中标出点B的位置,它坐标是( , ) ●A(-2,1)-7●●●3.将点A向左平移2个单位长度,再向下平移4个单位长度得到点C,请你在坐标系中标出点C的位置,它坐标是( , ) ●A(-2,1)-75.如果将点A向左
平移h个单位长度,再向下平移k个单位长度得到点D,那么点D坐标是( , ) 4.把点A(-2,1)进行怎样的平移可以得到点E ( 5 , -4 ) E ( 5 , -4 ) ●1.将点A(3,2)向上平移2个单位长度,
得到A’,则A’的坐标为______.
2.将点A(3,2)向下平移3个单位长度,
得到A’,则A’的坐标为______.
3.将点A(3,2)向左平移4个单位长度,
得到A’,则A’的坐标为______.(3,4)4.点A’(6,3)是由点A(-2,3)经过____
______________得到的.点B(4,3)
向______________得到B’(6,3)
5.课本P171 练习第2题右平移2个单位长度小试牛刀(3,-1)(-1,2)122、在平面直角坐标系中,有一点P(-4,2),(1)若将P先向右平移5个单位长度,再向上平移3个单位长度,所得坐标为_______。(-1,7)小荷才露尖尖角(2)若将P先向上平移3个单位长度,再向右平移5个单位长度,所得坐标为_______
(3)已知点A(-4,-6),将点A先向右平移4个单位长度,再向上平移6个单位长度,得到A′,则A′的坐标为________.。(1,5)(-7,-2)
例4 如图,⊿ABC的顶点坐标分别为A(-3,3),
B(2,3),C(0,5),平移⊿ABC得到⊿A`B`C`,
已知点A`的坐标是(0,-2)BA`●(1)求点B`,C`的坐标;
(2)画出⊿A`B`C`;
(3) ⊿A`B`C`可以由
⊿ABC经过一次平移得
到吗?如果能,请在图
中标出平移的方向,并
求出平移的距离.B`解 (1) 如图,因为点A与点A`的坐标分别是
(-3,3)与(0,-2),由
0-(-3)=3,-2-3=-5
可知,点A`可以看作是将点A先向右平移3个单位长度,再向下平移5个单位长度得到的.从而,点B`,C`可以看作是将点B,C分别进行了同样的平移而得到的.所以,点B`的坐标为(2+3,3+(-5)),即(5,-2);点C`的坐标为(0+3,5+(-5)),即(3,0);
(2)分别作出点B`,C`,顺次连接A`B`,B`C`,C`A`,就得到⊿A`B`C`.
ABCA`●C`小结今天你有什么收获? 1、知道了在平面直角坐标系内,将点
P(x,y)向左、右、上、下平移a 个
单位长度后,对应点的坐标变化情况.2、将图形平移时就是将关键点进行平
移,再顺次连接各关键点.向左平移
a个单位向右平移
a个单位小结P(x, y)P(x, y-b)P(x, y+b)P(x-a, y)P(x+a, y)(2012山东青岛)如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A1的坐标是【 】
A.(6,1) B.(0,1) C.(0,-3) D.(6,-3)B2、(2013?广安)将点A(﹣1,2)沿x轴向右平移3个单位长度,再沿y轴向下平移4个长度单位后得到点A′的坐标为 .(2,﹣2)3、(2012辽宁铁岭)如图,在平面直角坐标系中,△ABC经过平移
后点A的对应点为点A′,则平移后点B的对应点B′的坐标为 .(﹣2,1) 3、如图,三角形AOB沿x轴向右平移3个单位后,得到三角形CDE,则三角形CDE的三个顶点坐标为多少?xyAB(2013?昆明)在平面直角坐标系中,四边形ABCD的位置如图所示,解答下列问题:
将四边形ABCD先向左平移4个单位,再向下平移6个单位,得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1;并写出各顶点的坐标。4、(2011黑龙江大庆)在平面直角坐标系中,已知点A(-1,0)和B(1,2),连接AB,平移线段AB得到线段A1B1.若点A的对应点A1的坐标为(2,-1),则点B的对应点B1的坐标为
A.(4,3) B.(4,1) C.(-2,3) D.(-2,1)
5、如图,把图①中的△ABC经过一定的变换得到图②中的△A′B′C′,如果图①中△ABC上点P的坐标为(a,b),那么这个点在图②中的对应点P′的坐标为( ) A.(a-2,b-3) B.(a-3,b-2)
C.(a+3,b+2) D.(a+2,b+3) 6、在平面直角坐标系中,□ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7);B.(5,3) C.(7,3);D.(8,2)作业课本P172 习题11.1
4 、5、61、如图所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分-别是( )
A.∠F, AC B.∠BOD, BA; C.∠F, BA D.∠BOD, AC
2、在平移过程中,对应线段( )
A.互相平行且相等; B.互相垂直且相等
C.互相平行(或在同一条直线上)且相等3、如图所示,平移△ABC可得到△DEF,如果∠A=50°,
∠C=60°,那么∠E=____-度,∠EDF=_______度,
∠F=______度,∠DOB=_______度.(2013四川宜宾)如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为 .15解:设点A到BC的距离为h,则S△ABC=BC?h=5,
∵平移的距离是BC的长的2倍,
∴AD=2BC,CE=BC,
∴四边形ACED的面积=(AD+CE)?h
=(2BC+BC)?h
=3×BC?h=3×5
=15.(2012湖南湘潭)如图,△ABC是边长为3的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于F.
(1)猜想AC与BD的位置关系,并证明你的结论;
(2)求线段BD的长.解:(1)AC⊥BD。证明如下:
∵△DCE由△ABC平移而成,
∴△DCE≌△ABC。
又∵△ABC是等边三角形,
∴BC=CD=CE=DE,∠E=∠ACB=60°。
∴∠DBC=∠BDC=30°
∴∠BDE=90°。
∵BD⊥DE,
∵∠E=∠ACB=60°,
∴AC∥DE。∴BD⊥AC。。(2)在Rt△BED中,∵BE=6,DE=3,
∴
一定的距离,图形的这种变化叫做平移。
平移只改变图形的 不改变图形的 。位置形状和大小平移定义:平移性质 一个图形和它经过平移所得的图形中,一个图形和它平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等;1、如图将ΔABC水平向右平移到ΔDEF,
若A、D间的距离为1,CE=2,则BF=( )
A、3 B、4 C、5 D、不能确定
2、(2010?揭阳)在下面的格子里,虚线表示平移的起点,实线图表示平移的终点.平移了( )格.
A.14 B.17 C.20 D 16BB(2013山东滨州)如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是( ) A. 0 B.1 C.2 D. 3D. (2012浙江义乌)如图,将周长为8的△ABC沿BC方向平移1个
单位得到△DEF,则四边形ABFD的周长为【 】 A.6 B.8 C.10 D.12C 根据题意,将周长为8个单位的等边△ABC沿边BC向右平移1个单位得到△DEF,
∴AD=1,BF=BC+CF=BC+1,DF=AC。
又∵AB+BC+AC=8,
∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10。
故选C。如图,将点A(-2,-3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.把点A向左平移2个单位呢?xyO12342413-1-2-3-4-5-1-2-3-4-55-6A1(3, -3)A(-2,-3)把点A向上平移6个单位呢?A2(-4,-3)把点A向下平移4个单位呢?A3(-2,3)A4(-2,-7)(-2,-3)右移5个单位(3,-3)横坐标+5(-2,-3)左移2个单位(-4,-3)横坐标-2(-2,-3)上移6个单位(-2,3)纵坐标+6(-2,-3)下移4个单位(-2,-7)纵坐标-4探究:平移前后的坐标有什么关系?点的平移归纳:点(x,y)左右平移a个单位长度(x-a,y)点(x,y)上下平移b个单位长度纵变横不变横变纵不变左减(x+a,y)右加(x,y+b)上加(x,y-b)下减向右平移
a个单位向左平移
a个单位归纳P(x, y)P(x-a, y)P(x+a, y)P(x, y+b)P(x, y-b)左减右加上加下减1.将点A分别向上、向下、向左、向右平移5个单位长度,所得到的点的坐标分别是( , )( , )
( , )( , ) 阅读课本169—171页交流与发现,完成下列问题●A(-2,1)-72.将点A向右平移5个单位长度,再向上平移3个单位长度得到点B,请你在坐标系中标出点B的位置,它坐标是( , ) ●A(-2,1)-7●●●3.将点A向左平移2个单位长度,再向下平移4个单位长度得到点C,请你在坐标系中标出点C的位置,它坐标是( , ) ●A(-2,1)-75.如果将点A向左
平移h个单位长度,再向下平移k个单位长度得到点D,那么点D坐标是( , ) 4.把点A(-2,1)进行怎样的平移可以得到点E ( 5 , -4 ) E ( 5 , -4 ) ●1.将点A(3,2)向上平移2个单位长度,
得到A’,则A’的坐标为______.
2.将点A(3,2)向下平移3个单位长度,
得到A’,则A’的坐标为______.
3.将点A(3,2)向左平移4个单位长度,
得到A’,则A’的坐标为______.(3,4)4.点A’(6,3)是由点A(-2,3)经过____
______________得到的.点B(4,3)
向______________得到B’(6,3)
5.课本P171 练习第2题右平移2个单位长度小试牛刀(3,-1)(-1,2)122、在平面直角坐标系中,有一点P(-4,2),(1)若将P先向右平移5个单位长度,再向上平移3个单位长度,所得坐标为_______。(-1,7)小荷才露尖尖角(2)若将P先向上平移3个单位长度,再向右平移5个单位长度,所得坐标为_______
(3)已知点A(-4,-6),将点A先向右平移4个单位长度,再向上平移6个单位长度,得到A′,则A′的坐标为________.。(1,5)(-7,-2)
例4 如图,⊿ABC的顶点坐标分别为A(-3,3),
B(2,3),C(0,5),平移⊿ABC得到⊿A`B`C`,
已知点A`的坐标是(0,-2)BA`●(1)求点B`,C`的坐标;
(2)画出⊿A`B`C`;
(3) ⊿A`B`C`可以由
⊿ABC经过一次平移得
到吗?如果能,请在图
中标出平移的方向,并
求出平移的距离.B`解 (1) 如图,因为点A与点A`的坐标分别是
(-3,3)与(0,-2),由
0-(-3)=3,-2-3=-5
可知,点A`可以看作是将点A先向右平移3个单位长度,再向下平移5个单位长度得到的.从而,点B`,C`可以看作是将点B,C分别进行了同样的平移而得到的.所以,点B`的坐标为(2+3,3+(-5)),即(5,-2);点C`的坐标为(0+3,5+(-5)),即(3,0);
(2)分别作出点B`,C`,顺次连接A`B`,B`C`,C`A`,就得到⊿A`B`C`.
ABCA`●C`小结今天你有什么收获? 1、知道了在平面直角坐标系内,将点
P(x,y)向左、右、上、下平移a 个
单位长度后,对应点的坐标变化情况.2、将图形平移时就是将关键点进行平
移,再顺次连接各关键点.向左平移
a个单位向右平移
a个单位小结P(x, y)P(x, y-b)P(x, y+b)P(x-a, y)P(x+a, y)(2012山东青岛)如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A1的坐标是【 】
A.(6,1) B.(0,1) C.(0,-3) D.(6,-3)B2、(2013?广安)将点A(﹣1,2)沿x轴向右平移3个单位长度,再沿y轴向下平移4个长度单位后得到点A′的坐标为 .(2,﹣2)3、(2012辽宁铁岭)如图,在平面直角坐标系中,△ABC经过平移
后点A的对应点为点A′,则平移后点B的对应点B′的坐标为 .(﹣2,1) 3、如图,三角形AOB沿x轴向右平移3个单位后,得到三角形CDE,则三角形CDE的三个顶点坐标为多少?xyAB(2013?昆明)在平面直角坐标系中,四边形ABCD的位置如图所示,解答下列问题:
将四边形ABCD先向左平移4个单位,再向下平移6个单位,得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1;并写出各顶点的坐标。4、(2011黑龙江大庆)在平面直角坐标系中,已知点A(-1,0)和B(1,2),连接AB,平移线段AB得到线段A1B1.若点A的对应点A1的坐标为(2,-1),则点B的对应点B1的坐标为
A.(4,3) B.(4,1) C.(-2,3) D.(-2,1)
5、如图,把图①中的△ABC经过一定的变换得到图②中的△A′B′C′,如果图①中△ABC上点P的坐标为(a,b),那么这个点在图②中的对应点P′的坐标为( ) A.(a-2,b-3) B.(a-3,b-2)
C.(a+3,b+2) D.(a+2,b+3) 6、在平面直角坐标系中,□ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7);B.(5,3) C.(7,3);D.(8,2)作业课本P172 习题11.1
4 、5、61、如图所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分-别是( )
A.∠F, AC B.∠BOD, BA; C.∠F, BA D.∠BOD, AC
2、在平移过程中,对应线段( )
A.互相平行且相等; B.互相垂直且相等
C.互相平行(或在同一条直线上)且相等3、如图所示,平移△ABC可得到△DEF,如果∠A=50°,
∠C=60°,那么∠E=____-度,∠EDF=_______度,
∠F=______度,∠DOB=_______度.(2013四川宜宾)如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为 .15解:设点A到BC的距离为h,则S△ABC=BC?h=5,
∵平移的距离是BC的长的2倍,
∴AD=2BC,CE=BC,
∴四边形ACED的面积=(AD+CE)?h
=(2BC+BC)?h
=3×BC?h=3×5
=15.(2012湖南湘潭)如图,△ABC是边长为3的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于F.
(1)猜想AC与BD的位置关系,并证明你的结论;
(2)求线段BD的长.解:(1)AC⊥BD。证明如下:
∵△DCE由△ABC平移而成,
∴△DCE≌△ABC。
又∵△ABC是等边三角形,
∴BC=CD=CE=DE,∠E=∠ACB=60°。
∴∠DBC=∠BDC=30°
∴∠BDE=90°。
∵BD⊥DE,
∵∠E=∠ACB=60°,
∴AC∥DE。∴BD⊥AC。。(2)在Rt△BED中,∵BE=6,DE=3,
∴
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
